#1568. [2020提高组十连测day5]白银御行

哇偶...

畸形第k大->

二分答案

多次询问->

整体二分

然后考虑怎么把矩阵相交变成数点问题

两个矩阵相交的条件可以是在两维都要区间相交

而转换...最好用的消除条件的方法就是容斥

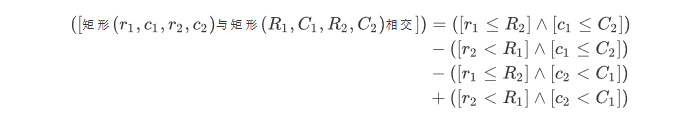
所以也就是说我们按照这个条件去处理每一层的整体二分过程就好了

问题在于代码有好多好多细节QAQ

堪比接水果

注意 :

多开几个数组处理每一层询问和修改的分开
注意最后值域收缩到一个点那些点的答案就是这个值
注意最小化所以<=分左边

code:


//Finished by dawn light
//as difficult as frute
//qwq orzmyh!
#include<bits/stdc++.h>
const int MAXN = 1e5 + 7 + 1e4;
using namespace std;

int n, m;
struct mat {
	int r1, c1, r2, c2, z, id;
	bool operator<(const mat &x)const {
		return c1 == x.c1 ? z < x.z : c1 < x.c1;
	}
} e[MAXN], ask[MAXN], mdq[MAXN * 2], a[MAXN], b[MAXN];

struct rec {
#define lowbit(x) (x&(-x))
	int tr[MAXN * 2];
	inline void mdf(int x, int V) {
		for(; x <= n; x += lowbit(x))tr[x] += V;
	}
	inline int qry(int x) {
		int ret = 0;
		for(; x; x -= lowbit(x))ret += tr[x];
		return ret;
	}
} tr;
int tp[MAXN];

inline void pd1(int L, int R, int l, int r, int P) {
	int tot = 0;
	for(int i = L; i <= R; ++i) {
		if(e[i].id <= P) {
			mdq[++tot] = e[i];
			mdq[tot].r1 = e[i].r1;
			mdq[tot].c1 = e[i].c1;
			mdq[tot].z = -2;
		}
	}
	for(int i = l; i <= r; ++i) {
		mdq[++tot] = ask[i];
		mdq[tot].r1 = ask[i].r2;
		mdq[tot].c1 = ask[i].c2;
	}
	sort(mdq + 1, mdq + tot + 1);
	for(int i = 1; i <= tot; ++i) {
		if(mdq[i].z == -2) {
			tr.mdf(mdq[i].r1, 1);
		} else {
			tp[mdq[i].id] += tr.qry(mdq[i].r1);
		}
	}
	for(int i = 1; i <= tot; ++i)
		if(mdq[i].z == -2) {
			tr.mdf(mdq[i].r1, -1);
		}
}

inline void pd2(int L, int R, int l, int r, int P) {
	int tot = 0;
	for(int i = L; i <= R; ++i) {
		if(e[i].id <= P) {
			mdq[++tot] = e[i];
			mdq[tot].r1 = e[i].r2;
			mdq[tot].c1 = e[i].c1;
			mdq[tot].z = -2;
		}
	}
	for(int i = l; i <= r; ++i) {
		mdq[++tot] = ask[i];
		mdq[tot].r1 = ask[i].r1 - 1;
		mdq[tot].c1 = ask[i].c2;
	}
	sort(mdq + 1, mdq + tot + 1);
	for(int i = 1; i <= tot; ++i) {
		if(mdq[i].z == -2) {
			tr.mdf(mdq[i].r1, 1);
		} else {
			if(mdq[i].r1 == 0)continue;
			tp[mdq[i].id] -= tr.qry(mdq[i].r1);
		}
	}
	for(int i = 1; i <= tot; ++i)if(mdq[i].z == -2)tr.mdf(mdq[i].r1, -1);
}

inline void pd3(int L, int R, int l, int r, int P) {
	int tot = 0;
	for(int i = L; i <= R; ++i) {
		if(e[i].id <= P) {
			mdq[++tot] = e[i];
			mdq[tot].r1 = e[i].r1;
			mdq[tot].c1 = e[i].c2;
			mdq[tot].z = -2;
		}
	}
	for(int i = l; i <= r; ++i) {
		mdq[++tot] = ask[i];
		mdq[tot].r1 = ask[i].r2;
		mdq[tot].c1 = ask[i].c1 - 1;
	}
	sort(mdq + 1, mdq + tot + 1);
	for(int i = 1; i <= tot; ++i) {
		if(mdq[i].z == -2) {
			tr.mdf(mdq[i].r1, 1);
		} else {
			tp[mdq[i].id] -= tr.qry(mdq[i].r1);
		}
	}
	for(int i = 1; i <= tot; ++i)if(mdq[i].z == -2)tr.mdf(mdq[i].r1, -1);
}

inline void pd4(int L, int R, int l, int r, int P) {
	int tot = 0;
	for(int i = L; i <= R; ++i) {
		if(e[i].id <= P) {
			mdq[++tot] = e[i];
			mdq[tot].r1 = e[i].r2;
			mdq[tot].c1 = e[i].c2;
			mdq[tot].z = -2;
		}
	}
	for(int i = l; i <= r; ++i) {
		mdq[++tot] = ask[i];
		mdq[tot].r1 = ask[i].r1 - 1;
		mdq[tot].c1 = ask[i].c1 - 1;
	}
	sort(mdq + 1, mdq + tot + 1);
	for(int i = 1; i <= tot; ++i) {
		if(mdq[i].z == -2) {
			tr.mdf(mdq[i].r1, 1);
		} else {
			if(mdq[i].r1 == 0)continue;
			tp[mdq[i].id] += tr.qry(mdq[i].r1);
		}
	}
	for(int i = 1; i <= tot; ++i)if(mdq[i].z == -2)tr.mdf(mdq[i].r1, -1);
}

inline void fz(int vL, int vR, int L, int R, int l, int r) {
	if(vL == vR) {
		for(int i = l; i <= r; ++i) {
			tp[ask[i].id] = vL;
		}
		return;
	}
	int M = (vL + vR) >> 1;
	for(int i = l; i <= r; ++i)tp[ask[i].id] = 0;
	pd1(L, R, l, r, M);
	pd2(L, R, l, r, M);
	pd3(L, R, l, r, M);
	pd4(L, R, l, r, M);
	int T1 = 0;
	int T2 = 0;
	for(int i = l; i <= r; ++i) {
		if(tp[ask[i].id] >= ask[i].z) {
			a[++T1] = ask[i];
		} else {
			b[++T2] = ask[i];
			b[T2].z -= tp[ask[i].id];
		}
	}
	int tmp1 = l + T1 - 1;
	for(int i = l; i <= tmp1; ++i) {
		ask[i] = a[i - l + 1];
	}
	for(int i = tmp1 + 1; i <= r; ++i) {
		ask[i] = b[i - tmp1];
	}
	T1 = 0;
	T2 = 0;
	for(int i = L; i <= R; ++i) {
		if(e[i].id <= M) {
			a[++T1] = e[i];
		} else {
			b[++T2] = e[i];
		}
	}
	int tmp2 = L + T1 - 1;
	for(int i = L; i <= tmp2; ++i) {
		e[i] = a[i - L + 1];
	}
	for(int i = tmp2 + 1; i <= R; ++i) {
		e[i] = b[i - tmp2];
	}
	if(l <= tmp1)fz(vL, M, L, tmp2, l, tmp1);
	if(r >= tmp1 + 1)fz(M + 1, vR, tmp2 + 1, R, tmp1 + 1, r);
	return ;
}

inline void solve2() {
	fz(1, n + 1, 1, n, 1, m);
	for(int i = 1; i <= m; ++i) {
		if(tp[i] > n)puts("-1");
		else printf("%d\n", tp[i]);
	}
	return ;
}
namespace fastIO {
#define BUF_SIZE (1<<22)
	static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = BUF_SIZE + buf;
	inline char nc() {
		if(p1 == pend) {
			p1 = buf;
			pend = buf + fread(buf, 1, BUF_SIZE, stdin);
		}
		return *p1++;
	}
	inline int read() {
		int x = 0;
		char s = nc();
		for(; !isdigit(s); s = nc());
		for(; isdigit(s); s = nc())x = (x << 1) + (x << 3) + s - '0';
		return x;
	}
}
using namespace fastIO;
int main() {
	n = read();
	m = read();
	for(int i = 1; i <= n; ++i) {
		e[i].r1 = read();
		e[i].c1 = read();
		e[i].r2 = read();
		e[i].c2 = read();
		e[i].id = i;
	}
	for(int i = 1; i <= m; ++i) {
		ask[i].r1 = read();
		ask[i].c1 = read();
		ask[i].r2 = read();
		ask[i].c2 = read();
		ask[i].z = read();
		ask[i].id = i;
	}
	solve2();
	return 0;
}

夏晓光(loveJY)的博客

#1568. [2020提高组十连测day5]白银御行

CSP-S2考前综合强化刷题（第一场)