夏晓光(loveJY)的博客

仍要向下扎根,向上结果

首页 归档 标签 关于 友链

20zr暑期AB班十连测day10

2020-08-06 13 min read # 凸包拟合 # 均摊 # 线性代数 # 容斥 # bitset # 线段树

自闭了,没有不会被卡的我

C

直接在线吧...

一个区间当所有数都不会被修改时我们就不做gcd了,就是意味着区间aia_i|x

等价于lcmailcm_{a_i}|x就不会被修改...

线段树维护每个区间的LCM,如果不是x的约数就不递归,否则就递归下去

显然一个数最多被修改log次

每次看一个区间是不是x的因子,是的话一定有lcm不整除那个x

code:



//From Dawn light
//Ultimate Destroy
//狛枝就是菜!
#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
#define uint unsigned int
const int MAXN = 2e5 + 7;
const int MAXM = 5e5 + 7;
const int MAXT = 6e5 + 7;//3倍空间
using namespace std;

int n, m;
ll a[MAXN];

inline ll gcd(ll x, ll y) {
	return (y == 0) ? x : gcd(y, x % y);
}

//均摊复杂度正确
//一类区间:16,16,16,16,16 修改为16
//满足性质:min==max==gcdmax,change
//二类区间:4,8,4,8,4,8 修改为8
//满足性质:只修改一次,即我们只记住一下的即可
//三类区间:1111111111 修改为123,234,345....
//满足性质:只修改0次
//还有个性质:区间LCM>1e18...感觉意义不大
//三被1包含了...但是问题不大qwq
struct rec {
	ll tag, maxx, minx, ccnt, sum, LCM;
} tr[MAXT];

inline ll lcm(ll x, ll y) {
	if((__int128)x / gcd(x, y) * y > 1e18)return 1e18 + 1;
	return x / gcd(x, y) * y;
}

namespace seg {
	int T, root;
	int ls[MAXT], rs[MAXT];
#define lson ls[k]
#define rson rs[k]
#define mid ((l+r)>>1)
	inline void pushup(int k) {
		tr[k].maxx = max(tr[lson].maxx, tr[rson].maxx);
		tr[k].minx = min(tr[lson].minx, tr[rson].minx);
		tr[k].sum = tr[lson].sum + tr[rson].sum;
		tr[k].LCM = lcm(tr[lson].LCM, tr[rson].LCM);
	}
	inline void built(int &k, int l, int r) {
		if(!k)k = ++T;
		if(l == r) {
			tr[k].maxx = tr[k].minx = tr[k].sum = tr[k].LCM = a[l];
			return;
		}
		built(lson, l, mid);
		built(rson, mid + 1, r);
		pushup(k);
	}
	inline void modify(int k, int l, int r, int L, int R, ll V) {
		if(l == r) {
			tr[k].sum = gcd(tr[k].sum, V);
			tr[k].maxx = tr[k].sum;
			tr[k].minx = tr[k].sum;
			tr[k].LCM = tr[k].sum;
			return ;
		}
		if(l >= L && r <= R) {
			if(V % tr[k].LCM != 0) {
				tr[k].LCM = gcd(tr[k].LCM, V);
			} else {//没了
				return ;
			}
		}
		if(L <= mid)modify(lson, l, mid, L, R, V);
		if(R > mid)modify(rson, mid + 1, r, L, R, V);
		pushup(k);
	}
	inline uint query(int k, int l, int r, int L, int R) {
		if(L <= l && R >= r) {
			return tr[k].sum;//自动取模?
		}
		if(R <= mid)return query(lson, l, mid, L, R);
		else if(L > mid)return query(rson, mid + 1, r, L, R);
		else return query(lson, l, mid, L, R) + query(rson, mid + 1, r, L, R);
	}
}
using namespace seg;

int main() {
	// freopen("test.in", "r", stdin);
	// freopen("test1.out", "w", stdout);
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; ++i) {
		scanf("%lld", &a[i]);
	}
	built(root, 1, n);
	for(ll i = 1, typ, x, y, z; i <= m; ++i) {
		scanf("%d", &typ);
		if(typ == 1) {
			scanf("%d%d%lld", &x, &y, &z);
			modify(root, 1, n, x, y, z);
		} else {
			scanf("%d%d", &x, &y);
			printf("%lld\n", query(root, 1, n, x, y));
		}
	}
	return 0;
}

A

怎么做到40pts啊?

显然是12+22...+(p−1)21^2+2^2...+(p-1)^2

x^2=a(mod P)

一定会有一个值小于等于(P-1)/2,一个解是x0x_0,另一个就是P−x0P-x_0

所以我们可以直接算一下这个值然后加起来...

但是要卡常就要优化取模...

x+=2*i-1

if(x>mod) x-=mod;

这样我们x就可以从S2跳到(S+1)2

P%4==1

-1是二次剩余

a是二次剩余的话P-a也是二次剩余...

发现我们可以打表...

那么我们就可以输出(p-1)/4*p即可...

ans=∑i2−∑i2p∗pans=\sum_{i^2}-\sum{\frac {i^2} {p}}*p

怎么算\sum{\frac i^2 p}

就可以考虑拿凸包去逼近这个曲线...如果可以就能得到一个n^{2/3}的做法了

额...感觉好抽象啊....

我们可以边在树上bfs边把凸包画出来...

然后考虑我们有一条严格在凸包上的线,这条线下面所有点都在曲线内部!

这个严格是指满足下面式子的斜率最大的整点构成的曲线

dydx<=F(x+dx)′\frac {dy} {dx} <= F(x+dx)'

就是考虑我们不停的沿着边界走,一直走上取整,就不会露过任何点

而用整数去逼近防止走到曲线内部可以用SBT...

首先如果走到了曲线内部就考虑弹栈, 如果在外面就考虑sbt向右子树走一步看在不在里面

如果我们这个样走一步,能够贴住这个曲线(刚好满足上面的式子),我们就走这一步,否则就知道上一步一定是最优的就更加贴合....

额..其实代码里面有详解,主要分三步,求值,暂定可以,拟合曲线

code:


#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
#define ull unsigned long long
#define U128 __uint128_t
#define uint unsigned int
using namespace std;
const int MAXN = 1e5 + 7;
ll n;


namespace fastIO {
	int _C = -1, _Z;
	char _sr[1 << 21], _z[20];
	inline void Ot() {
		fwrite(_sr, 1, _C + 1, stdout), _C = -1;
	}
	inline void print(U128 x, char C) {
		if(_C > 1 << 20)Ot();
		while(_z[++_Z] = x % 10 + 48, x /= 10);
		while(_sr[++_C] = _z[_Z], --_Z);
		_sr[++_C] = C;
	}
}
using namespace fastIO;

struct ST {
	int que[MAXN][2];
	int tail;
	void pop() {
		tail--;
	}
	void push(int x, int y) {
		tail++;
		que[tail][0] = x;
		que[tail][1] = y;
	}
	void top(int &x, int &y) {
		x = que[tail][0];
		y = que[tail][1];
	}
} st;
//\sum_{i^2/p} 和 (x,y)
//凸包上方
inline int outside(ull x, ull y) {
	return (U128)y * n > (U128)x * x;
	//y>x^2/p
	//y*p>x^2
}
//f(x)=i^2/p
//f(x)'=2*i/p
//切线斜率
inline int cut_off(ull x, uint dx, uint dy) {
	//2*x/p >= dy/dx
	//x*dx >= 2 * dy * p
	return (U128)n * dy <= 2 * (U128)x * dx;
}

int main() {
	scanf("%lld", &n);
	// puts("qwq");
	// printf("%lld\n", n);
	U128 ret = 0;
	int dx = 0, dy = 0, ux = 0, uy = 0, mx = 0, my = 0;
	int cnt = 0;
	ull x = 0, y = 1;
	st.push(0, 1);
	st.push(1, 0);
	ull w = n / 2;
	while(st.tail) {
		st.top(dx, dy);
		//如果我们已在上方
		while(outside(x + dx, y + dy) && x + dx <= w) {//不到一半...
			//dx是横着的一段距离
			//dy是竖着的
			ret += y * dx + ((ll)dy - 1) * (dx + 1) / 2;//三角形面积?/jk
			x += dx;
			y += dy;
			//再走一步qwq
			// printf("%lld %lld\n", x, y);
			cnt++;
		}
		if(x + dx > w)break;
		//走过了一半,再数就重复了
		if(x >= n)break;
		while(1) {
			st.pop();
			ux = dx;
			uy = dy;
			st.top(dx, dy);
			//如果当前怎么走都是阴间的
			// printf("%lld?%lld\n", dx, dy);
			if(outside(x + dx, y + dy))break;
			//上方了
		}
		while(1) {
			mx = ux + dx;
			my = uy + dy;
			// printf("%lld!%lld\n", mx, my);
			if(!outside(x + mx, y + my)) {//在下面了...
				if(cut_off(x + mx, dx, dy))break;
				//如果这一步斜率小了
				ux = mx;
				uy = my;
			} else st.push(dx = mx, dy = my);//还在上面就再来一次
		}
	}
	//没走完啊
	for(ull i = x + 1; i <= w; ++i)
		ret = ret + (U128)i * i / n;
	U128 z = (U128)(w) * (w + 1) * (2 * w + 1) / 6 - ret * n;
	//\sum{i^2}-\sum_{i^2\p}*p
	//这里转化回来了!!!
	print(z, '\n');
	Ot();
	return 0;
}

B

啊,5pts挂了...好心疼

对于30我们暴力就好了,用bitset记下这个点能去那些点就好了然后边就不重要了...

如果碰到想找到的就break

然后dag就是转化用容斥求个方案数qwq,这个数据好像很强...

f_i表示0~p_i就是一开始不经过的关键点的路径条数

fi=gSPi−∑f[j]g[j]pif_i=g_SP_i-\sum_{f[j]}g[j]p_i

其实就考虑第一个经过哪个...然后容斥掉

正解

对于一个可逆的矩阵可以在O(n^2k)加上一个秩为k的矩阵并求出可逆矩阵

修改一个点的入边出边就相当于矩阵上某一行均变为0,是一个秩为1的修改,这个可以在支持单点查询的时候很快

然后你妈的上定理了

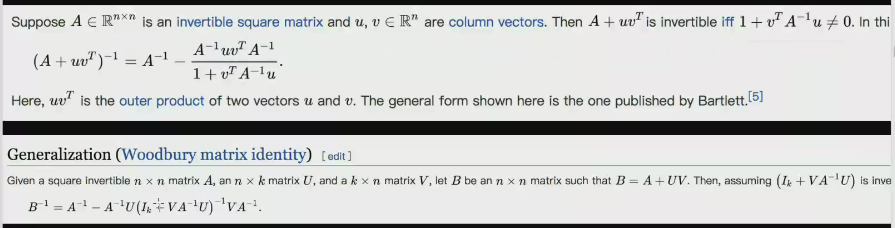
那么好像我们把整个图求个逆矩阵然后两两之间的逆矩阵可以拿出来,然后对于一组询问我们把中间的一个矩阵搞出来点乘一下,就能做到是否相互到达,复杂度是O(k13+k2k^2)

下面摘抄zhq的

DAG

考场最后40min想到的并不完全的做法。。会TTT。。然也没写完

以容斥计算方案数从而判断是否合法

然后应该就清楚了：容易 n3n^3 处理出 f[i][j]f[i][j] 从i到j的方案数。

然后我就想：用总方案数-经过一个禁止点的+经过两个的-经过三个的+。。。

经过若干禁止点S的方案数是可求的：一定按拓扑序经过，假设为S1，S2，S3，。。。Sx，那方案数就是 f[s][S1]∗f[S1][S2]∗f[S2][S3]∗...∗f[Sx][t]f[s][S1]* f[S1][S2]*f[S2][S3]*...*f[Sx][t] 。

对每个点的询问都要这么求，复杂度是 2k1∑k22^{k_1}\sum k_2​ ，刚刚好TTT。。、

事实上！容斥可以做到 O(k12)O(k_1^2) ！（64->36，但常数也小了不少）

换种思考方法：用总方案数减（从s不经过禁止点走到S1，再从S1随便走到t）减（从s不经过禁止点走到S2，再从S2随便走到t）减（从s不经过禁止点走到S3，再从S3随便走到t）...

然后“从s不经过禁止点走到Si”的方案数就是从s走到Si的总方案数减减（从s不经过禁止点走到S1，再从S1随便走到Si）减（从s不经过禁止点走到S2，再从S2随便走到Si）-...（从s不经过禁止点走到 Si−1S_{i-1}​ ，再从 Si−1S_{i-1} 随便走到Si）的方案数。

所以我们可以 O(k12)O(k_1^2) 地处理出“从s不经过 S1...Si−1S_1...S_{i-1}​ 这些关键点走到 SiS_i​ 关键点的方案数”。。

事实上，你把柿子写一下，发现这拆开后和上面 2k12^{k_1}​ 的柿子一样。

是不是也有点容斥DP那味啊？？？就考虑所有集合中最大元素为i对最终答案产生的贡献——。。。

注意这一切都是建立在如果经过关键点那一定是按拓扑序经过的这一前提上。所以只能DAG用。。

通过考虑“第一个不合法的是谁”把 2k2^k 的容斥优化成Poly(k)

[HAOI2017]方案数仿佛和这个题一样

q<=1e5q<=1e5

是bitset乱搞。。可我乱搞技术太菜了。。

只想到“诶我会 n2w\frac{n^2}{w}​ ”预处理两个点间的可达性，别的不会了！！。

额。。你发现，点数很少，如果我们能快速地判断一条边通往的是不是一个已经走过的点，那判断一次的复杂度就从和m相关，变成和n相关。

那，如果用一个bitset记录哪些点还没走过，然后再和表示邻接矩阵的bitset and一下不就能快速找到了嘛！！

bitset里有俩函数可以帮助我萌找到所有为1的位置！见代码。

Powered by Gridea RSS