20zr暑期AB班十连测day3

考时思路+考后题解
A
首先想了想指数上做操作感觉不太行
然后思考能不能用用他的性质,比如说求和什么的
于是乎对于一个固定的r和右边那个确定,你会发现有唯一的一个l与之对应
因为但凡l之后还有可以的一定会导致区间和大于l
于是乎我们不难发现答案小于等于nlogV,因为如果大于的话一定存在一个r和对应了多个l
然后考虑对于一个r预处理那个l?可以二分!
不太行,这好像很正解
于是我们利用之前的那个结论就可以解决的部分了
再往上有两个问题,1是我们的x是哪log个,2是怎么二分
B
暴力,考虑可以剪枝
不难发现当某个今后也都是0了,所以就可以T掉了
考后std
A
首先这个x显然和区间的最大值比较接近,不会超过一个log!
然后考虑怎么判断这个式子是否成立,考虑随便选几个素数看是否mod左右一下是否相等
然后考虑有个max有两种做法,第一个是笛卡尔树,第二个是分治,第三个是单调栈!
这里用分治
假设最大值在右边...,枚举个右端点假设右边的最大值是M,那么x此时有M+log种
然后我们钦定右边的取到最大值,然后左边的不是最大值,这个可以双指针
然后我们从左边做差一下,因为右边的和已经为S了,左边的和就要是,因为双指针我们就一定知道
右端点右移时左端点也只会单调向左移动qwq一层复杂度就了
笛卡尔树就可以考虑把每个都变成前缀和然后大概率两两数不同所以就可以一开始就建出来然后查询即可qwq
就是说我们每次只走小的一侧
下面提供AC代码
code:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll P = 500000003453647861ll;
const int MAXN = 2e5 + 7;
int n, a[MAXN], lg2[MAXN];
ll s[MAXN], pre2[MAXN], fac2[MAXN], ans;
const int w = 32000;
inline ll ksm(ll a, ll b, ll p) {
ll ans = (a * b - (ll)((long double)a / p * b) * p) % p;
if(ans < 0)ans += p;
//运用公式m%p=m-(m/p)*p
return ans;
}
inline ll pow2(int x) {
return ksm(fac2[x % w], pre2[x / w], P);
}//光速幂
//原理:我们预处理根号值域的答案,然后对于一组询问,可以变成整块*散块的答案
inline void init() {
lg2[1] = 0;
for(int i = 2; i <= n; ++i) {
lg2[i] = lg2[i >> 1] + 1;
// printf("lg2:%d?%d\n", lg2[i], i);
}
fac2[0] = 1;
for(int i = 1; i <= w; ++i) {
fac2[i] = fac2[i - 1] * 2 % P;
}
pre2[0] = 1;
for(int i = 1; i <= w; ++i)
pre2[i] = ksm(fac2[w], pre2[i - 1], P) % P;
//整除qwq
// printf("%lld %lld %lld\n", fac2[10], fac2[w], pre2[1]);
for(int i = 1; i <= n; ++i) {
s[i] = (s[i - 1] + pow2(a[i])) % P;//前缀和
// printf("%lld %lld\n", s[i], pow2(a[i]));
}
}
namespace Hash {
const int mod = 3e5 + 7;
int home[mod], ccnt;
struct {
int nxt, w;
ll to;
} e[mod];
inline int &add(int x, ll y) {
ccnt++;
e[ccnt].to = y;
e[ccnt].nxt = home[x];
home[x] = ccnt;
e[ccnt].w = 0;
return e[ccnt].w;
}
int vis[mod], st[mod], tp;
int &get(ll x) {
int p = x % mod;
if(!vis[p])vis[st[++tp] = p] = 1;
for(int i = home[p]; i; i = e[i].nxt) {
if(e[i].to == x)
return e[i].w;
}
return add(p, x);
}
int qry(ll x) {
int p = x % mod;
if(!vis[p])return 0;
for(int i = home[p]; i; i = e[i].nxt) {
if(e[i].to == x) {
return e[i].w;
}
}
return 0;
}
void clear() {
for(int i = 1; i <= tp ; ++i) {
vis[st[i]] = 0;
home[st[i]] = 0;//快速清空
}
ccnt = 0;
tp = 0;
}
}
const int B = 20;
inline int ckma(int &x, int y) {
if(x < y)x = y;
return x;
}
inline int ckmi(int &x, int y) {
if(x > y)x = y;
return x;
}
void fz(int l, int r) {
if(l == r) {
ans++; return ;
}
int mid = (l + r) >> 1;
// printf("in fz :%d %d %d\n", l, r, mid);
int i, j, MAX, MIN;
Hash::clear();
MAX = 0;
MIN = 1e9;
for(i = mid + 1, j = mid + 1; j <= r; ++j) {
ckma(MAX, a[j]);
ckmi(MIN, a[j]);
while(l < i && a[i - 1] <= MAX) {
--i;
// ckmi(MIN, a[i]);
Hash::get(s[i - 1])++;//这个前缀压入hash
}
// printf("and l,r is :%d %d %d %d\n", i, j, a[i - 1], MAX);
if(MAX - MIN > j - i - 1)continue;
ll tmp = 0;
if(i <= mid) {
ll t = pow2(MAX + 1);
// printf("but ans is :%lld %lld %lld\n", MAX, MIN, t);
for(int x = MAX + 1; x <= MAX + lg2[j - i + 1]; ++x) {
tmp = Hash::qry((s[j] + P - t) % P);
// printf("value is :%lld %lld %lld %lld\n", x, t, tmp, (s[j] + P - t) % P);
ans += Hash::qry((s[j] + P - t) % P);
//查是否有合法前驱
t = 2 * t % P;
}
}
}
Hash::clear();
MAX = 0;
MIN = 1e9;
// puts("qwq");
for(i = mid, j = mid; l <= i; --i) {
ckma(MAX, a[i]);
ckmi(MIN, a[i]);
while(j < r && a[j + 1] < MAX) {//细节!!!!
++j;
// ckmi(MIN, a[i]);
Hash::get(s[j])++;
}
// printf("and l,r is :%d %d %lld %lld\n", i, j, a[j + 1], MAX);
if(MAX - MIN > j - i - 1)continue;
ll tmp = 0;
if(j > mid) {
ll t = pow2(MAX + 1);
// printf("but ans is :%lld %lld %lld\n", MAX, MIN, t);
for(int x = MAX + 1; x <= MAX + lg2[j - i + 1]; ++x) {
tmp = Hash::qry((s[i - 1] + t) % P);
ans += Hash :: qry((s[i - 1] + t) % P);
// printf("value is :%lld %lld %lld %lld\n", x, t, tmp, (s[i - 1] + t) % P);
t = 2 * t % P;
}
}
}
fz(l, mid);
fz(mid + 1, r);
}
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
init();
fz(1, n);
printf("%lld\n", ans);
return 0;
}
B
一个初始的对应了点,然后那些组合数加起来...
其实就是点(x,y)走到x轴一排点(0,0),(x,0)的方案数
有神仙把两个int压成一个longlong然后循环展开重载取模就n^2过十万......了
考虑先把y轴分块,把每个序列切成一条条的,y坐标相差w
然后把每个点走到底下的方案数记成一个数组f
如果我们求出了上面的一条的f方案数就能求出下面一条的g方案数
因为对于下面一条线的一个点i
然后两条之间的点怎么加入?相当于加上了你发现这个东西是全部都要变的
然后你会发现最后要加上就可以使得我们加上的东西变成这个是卷积的,是最多w的qwq
注意我们把整个数组要翻转一下!!
具体的

你考虑其中负的那个就是对应了计数个-1相乘,而偶数的则是mod P的花样写法
然后f数组应该乘上那个从那一行走下去的方案数
但是最后我们还要卷上一个东西
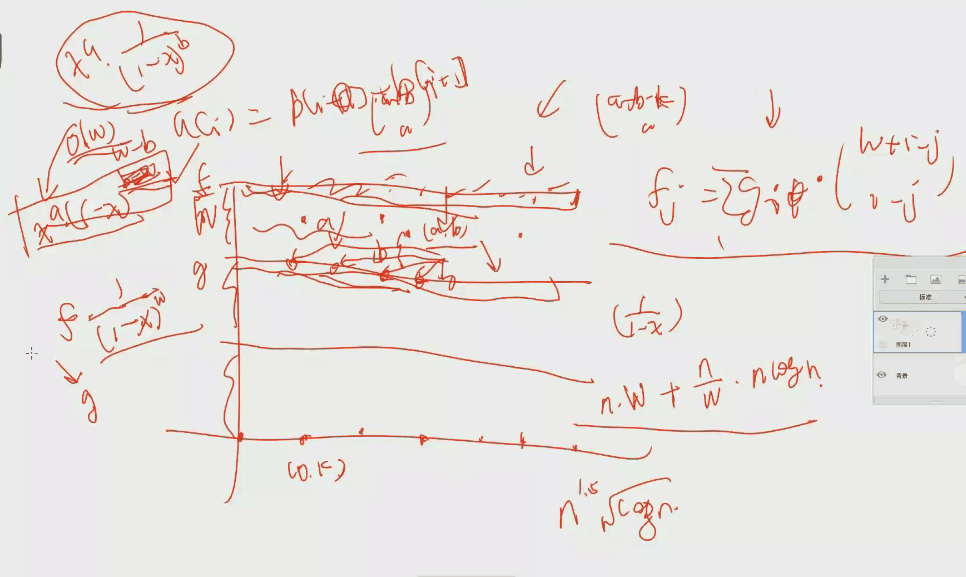
我承认还是不会,弃了弃了/se
暂切掉
code:
#include<bits/stdc++.h>
#define mkp(x,y) (make_pair(x,y))
#define ll long long
using namespace std;
const int MAXN = (1 << 18) + 5;
const int P = 998244353;
const int G0 = 332748118;
const int G1 = 3;
int n, a[MAXN], b[MAXN];
vector<pair<int, int> > v[MAXN];
inline ll ksm(ll x, int y) {
ll ans = 1;
while(y) {
if(y & 1)ans = ans * x % P;
x = x * x % P;
y >>= 1;
}
return ans;
}
inline void reduce(ll &x) {
x += x >> 31 & P;
}
int fac[MAXN], ifac[MAXN];
ll f[MAXN], g[MAXN], h[MAXN];
int C(int n, int k) {
return 1ll * fac[n] * ifac[k] % P * ifac[n - k] % P;
}
inline void Init() {
fac[0] = 1;
ifac[0] = 1;
for(int i = 1; i < MAXN; ++i)fac[i] = 1ll * fac[i - 1] * i % P;
ifac[MAXN - 1] = ksm(fac[MAXN - 1], P - 2);
for(int i = MAXN - 2; i; i--)ifac[i] = 1ll * ifac[i + 1] * (i + 1) % P;
ifac[1] = 1;
}
int L, len;
int R[MAXN];
void init(int n) {
len = 1;
while(len <= n) {
len <<= 1;
L++;
}
for(int i = 1; i < len; ++i) {
R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
}
return ;
}
void NTT(ll *F, int typ = 0) {
for(int i = 0; i < len; ++i)
if(i < R[i])swap(F[i], F[R[i]]);
int s, t;
for(int mid = 1; mid < len; mid <<= 1) {
ll wn = ksm(typ == -1 ? G0 : G1, (P - 1) / (mid << 1));
for(int j = 0; j < len; j += (mid << 1)) {
ll w = 1;
for(int k = 0; k < mid; ++k, w = wn * w % P) {
ll x = 1ll * F[j + k], y = 1ll * w * F[j + k + mid] % P;
F[j + k] = (1ll * x + y) % P;
F[j + k + mid] = (1ll * x - y + P) % P;
}
}
}
if(typ == -1) {
ll iv = ksm(len, P - 2);
for(int i = 0; i < len; ++i) {
F[i] = 1ll * F[i] * iv % P;
}
}
return ;
}
int main() {
scanf("%d", &n);
int B = sqrt(n * log(n)) + 1;
Init();
for(int i = 0; i < n; ++i) {
scanf("%d%d", &a[i], &b[i]);
a[i] = n - a[i] - 1;
b[i] = n - b[i] - 1;
v[a[i] / B].push_back(mkp(a[i], b[i]));
}
// printf("%d %d\n", C(5, 2), C(3, 1));
init(2 * n + 1);
for(int i = n / B; i >= 0; --i) {
if(!v[i].empty()) {
memset(f, 0, sizeof(f));
memset(g, 0, sizeof(g));
for(int j = 0; j <= i * B; ++j) {
f[j] = (j & 1 ? P - C(i * B, j) : C(i * B, j));
}
for(auto j : v[i]) {
int t = j.first % B;
// printf("%d %d %d\n", t, j.second + k, C(t, k));
for(int k = 0; k <= t; ++k) {
// printf("%d %d %d\n", t, j.second + k, C(t, k));
reduce(g[j.second + k] += (k & 1 ? -C(t, k) : C(t, k) - P));
}
}
// for(int j = 0; j < len; ++j) {
// printf("%d %d\n", g[j], f[j]);
// // h[j] = (h[j] + 1ll * f[j] * g[j] % P) % P;
// }
NTT(f);
NTT(g);
for(int j = 0; j < len; ++j) {
// printf("%d %d?\n", g[j], f[j]);
h[j] = (h[j] + 1ll * f[j] * g[j] % P) % P;
}
}
}
NTT(h, -1);
for(int i = 0; i < n; ++i)g[i] = 1ll * fac[i + n - 1] * ifac[n - 1] % P * ifac[i] % P;
for(int i = n; i < len; ++i)h[i] = g[i] = 0;
NTT(h);
NTT(g);
for(int i = 0; i < len; ++i)h[i] = 1ll * h[i] * g[i] % P;
NTT(h, -1);
for(int i = n - 1; i >= 0; --i)printf("%d ", h[i]);
puts("");
return 0;
}
C
两个点匹配的权值是他们中间的最大值,中间的那些数字是随机的,问最大权期望是多少
最直接找规律???每个元素在答案中的贡献只和他是第几大有关系
四个点你会发现最优的一定是下图中中间的那个
所以每四个点都要长成这样子
所以有n个点必然要前n/2和后面连接
然后问题变成了所有长度为n/2的最大值之和然后这个就可以发现他只和第几大有关系了(有多少个比他少)
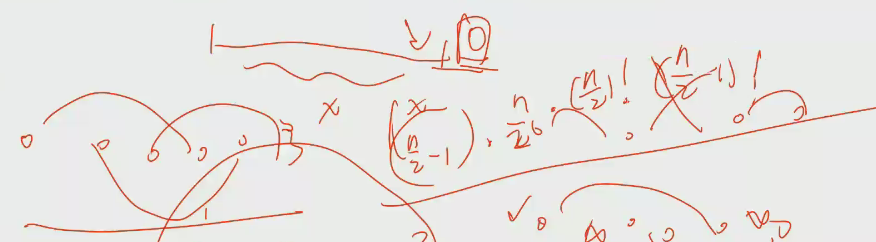
意思就是我们从比他小的选出n/2-1个构成,然后这一段再有n/2个位置可以放,然后再考虑其中顺序是有(n/2-1)!种,然后再考虑其他n/2个数随便排序为(n/2)!
code:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
const int MAXN = 3e5 + 7;
const int P = 998244353;
int n, a[MAXN];
inline ll ksm(ll x, ll y) {
ll ans = 1;
while(y) {
if(y & 1)ans = ans * x % P;
x = x * x % P;
y >>= 1;
}
return ans;
}
int fac[MAXN], ifac[MAXN];
inline ll C(int n, int m) {
return 1ll * fac[n] * ifac[m] % P * ifac[n - m] % P;
}
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; ++i)scanf("%d", &a[i]);
sort(a + 1, a + n + 1);
fac[0] = 1;
for(int i = 1; i <= n * 2; ++i) {
fac[i] = 1ll * fac[i - 1] * i % P;
}
ifac[n * 2] = ksm(fac[n * 2], P - 2);
for(int i = n * 2 - 1; i >= 2; --i) {
ifac[i] = 1ll * (i + 1) * ifac[i + 1] % P;
}
ifac[0] = 1;
ifac[1] = 1;
ll ans = 0;
int m = (n + 1) >> 1;
for(int i = m; i <= n; ++i) {
ll tmp = 1ll * C(i - 1, m - 1) * (m) % P;
tmp = tmp * fac[m] % P * fac[m - 1] % P;
ans = (ans + tmp * a[i] % P) % P;
}
printf("%lld\n", ans);
return 0;
}