夏晓光(loveJY)的博客

仍要向下扎根,向上结果

首页 归档 标签 关于 友链

20zr暑期AB班十连测day5

2020-08-01 16 min read # 启发式合并 # 后缀自动机 # 动态规划

A

设dpidp_i表示从点i开始的答案然后求和+最大值

直接写的话有30pts,用一个longlong可以记一下答案,但是这里是不能直接做的

显然DP不能优化,考虑优化转移

两个set比较的复杂度是O(min(S1,S2),logn)的,然后对于合并可以启发式合并,这个是均摊O(nlog2n)(nlog^2n)的

为啥写挂了?因为没有启发式合并啊

注意最大的那个数我们找出来后要打个*2标记然后加的时候就直接不考虑他就能保证复杂度不会被卡成O(n^2)了!!

而且我们父亲要继承最大的儿子才行/kk.


#include<cstdio>
#include<cstring>
#include<iostream>
#include<set>
using namespace std;
#define int long long
#define ll long long
const int P = 998244353;
const int MAXN = 1e5 + 7;
const int MAXM = 3e5 + 7;
int n, ccnt;
int home[MAXM], to[MAXM], nxt[MAXM], len[MAXM];
inline void ct(int x, int y, int z) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
	len[ccnt] = z;
}

inline ll ksm(ll x, int y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x;
		x = x * x;
		y >>= 1;
	}
	return ans;
}

ll dp[MAXN];
inline void dfs(int u, int F) {
	ll maxson = 0;
	for(int i = home[u]; i ; i = nxt[i]) {
		int v = to[i];
		if(v == F)continue;
		dfs(v, u);
		ll val = ksm(2, len[i]);
		dp[u] += dp[v] + val;
		maxson = max(dp[v] + val, maxson);
	}
	dp[u] += maxson;
	return ;
}
//queue?vector?set ba....
inline ll ksm2(ll x, ll y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}
set<int> st[MAXM]; //I am not afraid of TLE
int id[MAXM], tag[MAXM];
#define ins insert

inline int getf(int x) {
	return id[x] == x ? x : id[x] = getf(id[x]);
}

inline void add(int u, int x) {
	x -= tag[u];
	// printf("%d?%d\n", u, x);
	while(st[u].find(x) != st[u].end()) {
		st[u].erase(x);
		++x;
	}
	st[u].ins(x);//qwq?
	// printf("%d?%d?%d?\n", u, x, st[u].size());
}

inline int merge(int x, int y) {
	int qaq = min(st[x].size(), st[y].size());
	if(qaq == st[x].size()) {
		swap(st[x], st[y]);
		swap(tag[x], tag[y]);
	}
	// printf("merge : %d %d %d\n", x, y, qaq);
	for(auto it : st[y]) {
		add(x, it + tag[y]);
	}//fake启发式合并
	return x;
}

inline int pd(int x, int y) {
	auto itx = st[x].end();
	auto ity = st[y].end();
	if(st[y].size() == 0 && st[x].size() != 0)return 1;
	else if(st[y].size() == 0 && st[x].size() == 0)return 0;
	else if(st[x].size() == 0)return 0;
	itx--;
	ity--;
	// printf("%d %d\n", *itx, *ity);
	while((*itx) + tag[x] == (*ity) + tag[y] && (itx != st[x].begin()) && (ity != st[y].begin())) {
		// printf("%d %d\n", *itx, *ity);
		itx--;
		ity--;
	}
	// printf("%d %d\n", *itx, *ity);
	if((*itx) + tag[x] == (*ity) + tag[y] && st[x].size() <= st[y].size())//leny>lenx
		return 0;
	else if( (*ity) + tag[y] == (*itx) + tag[x] && st[y].size() < st[x].size())
		return 1;
	else return ((*itx) + tag[x]) > ((*ity) + tag[y]);
}

inline void dfs2(int u, int F) {
	// printf("%d %d %d!@#\n", u, F, id[u]);
	int maxid = 0;
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v == F)continue;
		// printf("%d???\n", v);
		dfs2(v, u);
		add(getf(v), len[i]);
		// printf("%d& %d?\n", getf(v), len[i]);
		if(getf(v) != getf(maxid) && pd(getf(v), getf(maxid))) {
			maxid = v;
		}
	}
	// printf("%d %d??\n", u, maxid);
	if(maxid)id[u] = getf(maxid);
	tag[getf(u)]++;
	// printf("%d?\n",)
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v == F)continue;
		if(maxid != v) {
			merge(getf(u), getf(v));
			// printf("%d %d!!\n", u, v);
		}
	}
	// ll ans = 0;
	// for(auto it : st[getf(u)]) {
	// 	// printf("%lld\n", it);
	// 	ans = (ans + ksm2(2, (it + tag[getf(u)])) % (P - 1)) % P;
	// }
	// printf("%lld\n", ans);
	return ;
}

inline void solve() {
	for(int i = 1; i <= n; ++i)id[i] = i;
	dfs2(1, 0);
	// puts("QAQ");
	ll ans = 0;
	for(auto it : st[getf(1)]) {
		// printf("%lld\n", it);
		ans = (ans + ksm2(2, (it + tag[getf(1)])) % (P - 1)) % P;
	}
	printf("%lld\n", ans);
	return ;
}


signed main() {
	// freopen("test.in", "r", stdin);
	// freopen("test.out", "w", stdout);

	scanf("%lld", &n);
	bool flg = 1;
	for(int i = 2, x, y; i <= n; ++i) {
		scanf("%lld%lld", &x, &y);
		if(y > 30)flg = 0;
		ct(x, i, y);
		ct(i, x, y);
	}
	// if(flg) {
	// 	dfs(1, 0);
	// 	printf("%lld\n", dp[1] % P);
	// } else {
	solve();
	// }
	return 0;
}

我都好调死了

C

考虑left表示前面加一个字符,right表示后面加一个

然后转移的时候就是在前缀树和后缀树上重新定位一下就能决定我们是在哪个方向加入字符了

就是ch和fa上

所以我们可以强制每个节点在左边加字符(向下走)走到最长的串,算出第一部分的答案,然后再考虑向后面加字符,这个就是一个后缀自动机上拓扑序DP一下

然后如果我们边有长度其实决定了我们可以等等再走,所以转移又会不太一样

code:


#include<cstdio>
#include<cstring>
#include<iostream>
#define R register
const int MAXN = 1e6 + 7;
const int MAXM = 5e5 + 7;
using std::max;
char s[MAXM];
int  c[MAXN], a[MAXN];
long long dp[MAXN];
int ch[MAXN][26], fa[MAXN], siz[MAXN], len[MAXN], T, lst;
inline void init() {
	T = lst = 1;
}
inline void ins(char c) {
	R int p = lst, np = lst = ++T;
	len[np] = len[p] + 1;
	siz[np] = 1;
	for(; !ch[p][c] && p; p = fa[p])ch[p][c] = np;
	if(!p) {
		fa[np] = 1;
	} else {
		R int q = ch[p][c];
		if(len[q] == len[p] + 1) {
			fa[np] = q;
		} else {
			R int nq = ++T;
			len[nq] = len[p] + 1;
			memcpy(ch[nq], ch[q], sizeof(ch[nq]));
			fa[nq] = fa[q];
			fa[q] = fa[np] = nq;
			for(; ch[p][c] == q; p = fa[p])ch[p][c] = nq;
		}
	}

}


int main() {
	scanf("%s", s + 1);
	int n = strlen(s + 1);
	init();
	R int i;
	for(i = 1; i <= n; ++i) {
		ins(s[i] - 'a');
	}
	for(i = 1; i <= T; ++i) {
		c[len[i]]++;
	}
	for(i = 1; i <= n; ++i) {
		c[i] += c[i - 1];
	}
	for(i = T; i >= 1; --i) {
		a[c[len[i]]--] = i;
	}
	for(i = T; i >= 2; --i) {
		siz[fa[a[i]]] += siz[a[i]];
	}
	dp[1] = 0;
	R int u, F, v;
	for(i = 1; i <= T; ++i) {
		u = a[i];
		F = fa[u];
		dp[u] = max(dp[u], dp[F] + (long long)siz[u] * (len[u] - len[F]));
		for(F = 0; F < 26; ++F) {
			if((v = ch[u][F]) != 0) {
				dp[v] = max(dp[v], dp[u] + (long long)siz[v] * (len[v] - len[u]));
			}
		}
	}
	printf("%lld\n", dp[lst]);
	return 0;
}

B

是个多项式算法都给您放过去

考场上我神仙的遇上了土豆电池T掉了

一个序列有多种划分方式,但是我们只需满足一种,所以就可以考虑容斥了!

然后对于前中后三段其实是可以考虑各种情况然后状压DP的....

然后考虑dp,dp_{i,j}表示前i个数经过了j个互不相等的数

1/231/321/32

则要经过dp(1,1)->dp(4,3)->dp(3,3)->dp(9,2)

这样子就是dp(a,a)−>dp(b,k)−>dp(n,>=b)dp(a,a)->dp(b,k)->dp(n,>=b)

如果n比较大,中间会有很长一段令人相同的限制,这些都一样就可以快速幂把它优化掉

就是乘上P(k,k)n−fi−edkP(k,k)^{\frac {n-fi-ed} {k}}

枚举fi,ed暴力用之前的dp计算fi和ed的方案数,中间再乘上这个即可qwq,然后记得要容斥就要乘上方案数

因为我们有一个fi就能算出ed了,所以只有本质不同的k个fi作为限制,然后用于容斥qwq

然后我们就可以得到2k∗(k2)2^k*(k^2)

然后又会发现我们有个第一段a,他要最大,就能转移到的最小的c最优

而且maxa能转移到minb,maxb能转移到minc,b是k2k或n-kn

这样每个状态都是O(k)种

然后我们发现他们可以通过一些长度小于k的方案数

从1->3,3->k-2再从k-2->1一直循环就是可以加速的

O(k5)O(k^5)实际状态数很少,压一压状态还可以更少??

对于n<=k的情况我们只需要枚举最大值和最小值然后前i个要求互补相同,后n-i个要求互不相同,i<n时有这样的而i>n的时候我们有(n,k)n!?

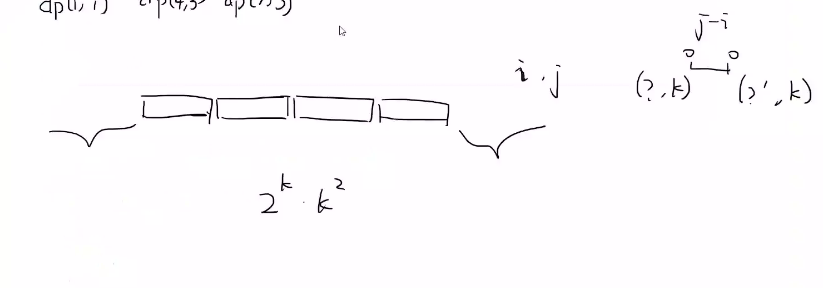
其实就是想我们有很多刀,然后通过拓扑dp从小到大一刀一刀的加入

考虑我们每次计入相邻两刀的计算方案,然后在统计答案的时候加入每一段的不同的限制

具体可以分成好几段

  1. 开头的刀刀之间 + 中途的加速部分的几段
  2. 开头到第一刀
  3. 最后一套限制到第一块加速开始的一段
  4. 最后一套最后一刀和n的一段

具体看代码吧,讲的相当清楚了/....\

code:



#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXW = 66;
const int P = 998244353;
int T;
int n, k, ans, tot;
int f[MAXW][MAXW][MAXW], fpre[MAXW][MAXW][MAXW];
int dp[MAXW][MAXW][MAXW][MAXW], g[MAXW][MAXW], lst[MAXW];
inline void init() {
	scanf("%d%d", &n, &k);
	memset(f, 0, sizeof(f));
	memset(fpre, 0, sizeof(fpre));
	memset(g, 0, sizeof(g));
	memset(dp, 0, sizeof(dp));
}

inline ll ksm(ll x, int y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

inline void add(int &x, int y) {
	x += y;
	if(x >= P)x -= P;
}


inline void initg() {
	int frm, stp, nw;
	//预处理部分,
	//第二维stp表示i,而nw表示j
	//frm是已知了前面一些数不同的填涂方案
	for(frm = 0; frm <= k; frm++) {
		f[frm][0][frm] = 1;
		for(stp = 0; stp <= k; ++stp) {
			for(nw = 0; nw <= k; ++nw) {
				if(f[frm][stp][nw]) {
					for(int nxt = 1; nxt <= nw; ++nxt)
						add(f[frm][stp + 1][nxt], f[frm][stp][nw]);
					add(f[frm][stp + 1][nw + 1],
						1ll * (k - nw) * f[frm][stp][nw] % P);
					// printf("frm:%d stp:%d now:%d f:%d\n", frm, stp, nw, f[frm][stp][nw]);
				}
			}
		}
	}
	for(int i = 0; i <= k; ++i) {
		for(int j = 0; j <= k; ++j) {
			for(int t = k; t >= 0; --t) {
				fpre[i][j][t] = f[i][j][t] + fpre[i][j][t + 1];
				if(fpre[i][j][t] >= P)fpre[i][j][t] -= P;
				//fpre是f的后缀和
				//就是至少t个不相同
			}
		}
	}
	for(int i = 0; i < k; ++i) {
		for(int j = 0; j < k; ++j) {
			if(i < j) {
				//这个是考虑两个中间的刀数
				//中间的限制是j-i
				int num = (n - j >= 0 ? (n - j) / k : 0);
				//然后会被统计num次
				g[i][j] = ksm(f[k][j - i][k], num);
			} else {//i>=j
				//这个是考虑两个之外的限制
				//每k个之间夹得之外的....|----|.....
				//....的部分
				//就是k-(i-j)
				//会被统计num次
				int num = (n - j - k >= 0 ? (n - j - k) / k : 0);
				g[i][j] = ksm(f[k][j + k - i][k], num);
			}
		}
	}
	for(int i = 0; i < k; ++i) {
		//论取模是如何自闭的
		//其实就是(n-i)%k....
		int x = (n - i >= 0 ? n - ((n - i) / k * k + i) : n);
		lst[i] = x;
		// printf("i=%d lst=%d\n", i, lst[i]);
	}
}

inline void solve() {
	for(int i = 0; i < k; ++i) {
		add(dp[i][i][lst[i]][lst[i]], 1);
	}
	ll ans = 0;
	for(int i = 0; i < k; ++i) {//第一块中最后一套限制i,i
		for(int fst = 0; fst <= i; ++fst) {//第一块中第一套限制fst,fst
			for(int mx = 0; mx < k; ++mx) {//最后一个数的最后一套限制,n,>=mx!!!
				for(int mn = 0; mn < k; ++mn) {//最后一块中第一套限制,n,>=mn
					if(dp[i][fst][mx][mn]) {
						int nw = dp[i][fst][mx][mn];
						if(i <= n) {
							int coef = 1ll * nw * f[0][i][i] % P * g[i][fst] % P;
							//首先第一步把i的限制加入然后再把第一块之外的限制加入
							if(k + fst <= n)
								coef = 1ll * coef * f[i][fst + k - i][k] % P;
							//如果k+fst<=n,说明我们至少存在中间限制的刀法
							//就是...fst-----i***|*fst+k----i+k.....
							//中间*部分的限制
							if(n - mn <= k)
								coef = 1ll * coef * fpre[n - mn][mn][mx] % P;
							//n-mn步是我们已知的,然后再填mn步使得mx个满足
							else  coef = 1ll * coef * fpre[k][mn][mx] % P;
							//...mn......n解决最后一段,大于k所以安心走
							ans += coef;
							if(ans > P)ans -= P;
						} else
							ans = (ans + 1ll * nw * f[0][n][n]) % P;
						//i>n直接容斥,让他满足这套限制
						for(int nxt = i + 1; nxt < k; ++nxt) {//下一套限制
							add(dp[nxt][fst][max(mx, lst[nxt])][min(mn, lst[nxt])],//这个转移非常能定夺mn,mx一切意义
								1ll * (P - nw) * g[i][nxt] % P//-nw * go i,nxt表示我们新加入了一刀,并计算了中间的贡献
							   );
						}
					}
				}
			}
		}
	}
	printf("%lld\n", ans);
}

int main() {
	scanf("%d", &T);
	while(T-- > 0) {
		init();
		initg();
		solve();
	}
	return 0;
}
Powered by Gridea RSS