夏晓光(loveJY)的博客

仍要向下扎根,向上结果

首页 归档 标签 关于 友链

20zr暑期AB班十连测day6

2020-08-02 11 min read # 树链剖分 # 容斥 # 线段树 # 字符串 # 动态规划

A

|S|=n

显然下面那个dp的答案是m*(m-1)^(n-1)

然后我们需要用二项式反演来容斥

ansi=C(m,i)∗(∑j(−1)jC(i,j)g(i))ans_i=C(m,i)*(\sum_{j} (-1)^j C(i,j) g(i))

zhq:显然可以NTT优化mlogm

自闭了....

K=1

答案相当于对于一个颜色i,有多少染色方案满足包括这个颜色

首先显然颜色之间没有本质区别,所以他们的方案数是一样的

然后问g1g_1?

这...显然是树形DP啊

你会发现这个DP是没法快速合并的qwq要自上而下去DP

首先对于每个子树规定一个点y

然后递归到y这个子树

所以各个儿子之间就互不影响了

fx,1f_{x,1}表示x的颜色已经定好,是否为1的情况下子树染色方案数

fx,0=∏fy,0(m−2)+fy,1f_{x,0}=\prod {f_{y,0}(m-2)+f_{y,1}}

fx,1=∏fy,0m−1f_{x,1}=\prod {f_{y,0}{m-1}}

x如果为S,f[x][1]=0f[x][1]=0

只能自上而下去搞是特别

k>1显然对于x^k我们有斯特林展开公式!

证明:

$$x^n=x^{n-1}*x$$

$$x^n=x \sum_{i=k}^{n-1} S(n-1,k) x^{k!} $$

$$x^n=\sum_{i=k}^{n-1} S(n-1,k) x^{k+1!} + \sum_{i=k}^{n-1} S(n-1,k) kx^{k}$$

把x^k下降幂提出来,里面就是斯特林数递推式

然后就能等于x^k的那个式子了

k!表示k次下降幂

变为∑c∑i=0kS(k,i)C(∣S(C)∣,i)\sum_c\sum_{i=0}^k {S(k,i)C(|S(C)|,i)}

∑i=0kS(k,i)∗i!∑cC(∣S(c)∣,i)\sum_{i=0}^k {S(k,i)*i!} \sum_c{C(|S(c)|,i)}

g=∑cC(∣S(C)∣,i)g=\sum_c{C(|S(C)|,i)}

如果后面的g能算出来就好了

∑c∑T,∣T∣=i[T∈S(C)]\sum_{c} \sum_{T,|T|=i} [T \in S(C)]

∑T,∣T∣=i∑c[T∈S(C)]\sum_{T,|T|=i} \sum_{c} [T \in S(C)]

就是i个颜色在关键点上都出现的方案数

令上面那个东西为h,所以g(i)=C(m,i)h(i)g(i)=C(m,i)h(i)

dp可以考虑容斥

我们可以考虑枚举有多少个颜色不在这里面,然后用一个容斥算出答案

h(i)=∑j=0i(−1)j(ji)dp[j]h(i)=\sum_{j=0}^i(-1)^j\binom {j} {i} dp[j]

dp[j]表示至少有j个不在S(c)中的方案数,即某个大小为j的集合ban满足与上S(c)为空集

f[x][0]f[x][0]是C_x不在ban里面的,1C_x表示在ban里面的

fxf_x的颜色是父亲定好的

转移式子

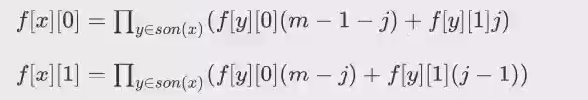
这个是父亲决定了儿子的颜色

统计答案

O(nk+k2)O(nk+k^2)

code:


#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 1e5 + 7;
const int P = 998244353;
const int MAXK = 88;
const int MAXM = 2e5 + 7;
int n, m, K, t;
int ccnt, nxt[MAXM], to[MAXM], home[MAXN];
inline void ct(int x, int y) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
	return ;
}
ll fac[MAXN], ifac[MAXN], h[MAXN], F[MAXN], g[MAXN], pix[MAXN];

inline ll C(int x, int y) {
	if(y < 0 || x < y)return 0;
	return 1ll * fac[x] * ifac[y] % P * ifac[x - y] % P;
}

inline ll ksm(ll x, ll y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

inline void add(int &x, ll y) {
	x += y;
	if(x >= P)x -= P;
}

int S[MAXK][MAXK];
inline void init() {
	fac[0] = 1;
	ifac[0] = ifac[1] = 1;
	for(int i = 1; i < MAXN; ++i) {
		fac[i] = 1ll * fac[i - 1] * i % P;
	}
	ifac[MAXN - 1] = ksm(fac[MAXN - 1], P - 2);
	for(int i = MAXN - 2; i; i--) {
		ifac[i] = 1ll * ifac[i + 1] * (i + 1) % P;
	}
	// printf("/yiw%lld %lld?", ifac[2] * 2 % P, fac[3]);
	S[0][0] = 1;
	for(int i = 1; i <= K; ++i) {
		for(int j = 1; j <= K; ++j) {
			add(S[i][j], S[i - 1][j - 1]);
			add(S[i][j], 1ll * S[i - 1][j] * j % P);
			// printf("%d ", S[i][j]);
		}
		// puts("");
	}
	return ;
}
int dp[MAXN][2];
inline void dfs(int u, int F, int B) {
	dp[u][0] = 1;
	dp[u][1] = pix[u] ^ 1;
	// printf("u%d F%d B%d\n", u, F, B);
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v == F)continue;
		dfs(v, u, B);
		int s0 = 0, s1 = 0;
		add(s0, 1ll * dp[v][0] * (m - 1 - B) % P);
		add(s0, 1ll * dp[v][1] * B % P);
		add(s1, 1ll * dp[v][0] * (m - B) % P);
		add(s1, 1ll * dp[v][1] * (B - 1) % P);
		dp[u][0] = 1ll * dp[u][0] * s0 % P;
		dp[u][1] = 1ll * dp[u][1] * s1 % P;
		// printf("az:%d %d\n", s0, s1);
	}
	// printf("get ans:%d %d\n", dp[u][0], dp[u][1]);
	return ;
}


int calc(int ban) {
	if(ban >= m)return 0;
	dfs(1, 0, ban);
	// printf("1,1:%d 1,0:%d\n", dp[1][1], dp[1][0]);
	int ret = (1ll * dp[1][1] * ban % P + 1ll * dp[1][0] * (m - ban) % P) % P;
	return ret;
}
inline void add(ll &x, ll y) {
	x += y;
	if(x >= P)x -= P;
}
int main() {
	scanf("%d%d%d%d", &n, &m, &K, &t);
	init();
	for(int i = 1, x; i <= t; ++i) {
		scanf("%d", &x);
		pix[x] = 1;
	}
	for(int i = 1, x, y; i < n; ++i) {
		scanf("%d%d", &x, &y);
		ct(x, y);
		ct(y, x);
	}
	for(int i = 0; i <= K; ++i) {
		F[i] = calc(i);
		// printf("%d %d\n", i, F[i]);
	}
	ll ans = 0;
	for(int i = 1; i <= K; ++i) {
		for(int j = 0; j <= i; ++j) {
			int coef = 1ll * F[j] * (j & 1 ? -1 : 1) * C(i, j) % P;
			add(coef, P);
			// printf("result%d %d %d\n", coef, (j & 1 ? -1 : 1), C(i, j));
			add(h[i], coef);
		}
		g[i] = 1ll * C(m, i) * h[i] % P;
		// printf("%d %d?\n", h[i], g[i]);
		add(ans, 1ll * S[K][i] * fac[i] % P * g[i] % P);
		// printf("but ->?%d %d %d\n", S[K][i], fac[i], g[i]);
	}
	printf("%lld\n", ans);
	return 0;
}

B

切开两个边会使得整个树变成三个连通块ABC

然后要求AB不连通,BC也不连通,就是把A+C和B之间的边割掉

d[x]表示子树x内连出去的边有几条因为LCA==1

然后您会发现dA+dC包含了子树A->C会较多,要减去cnt(A,C)

然后子树搞一个dfs序就变成了区间,放到平面上就可以二维前缀和优化!

然后发现会有一个割子节点和祖先的关系,这样挨着一定最优

这就意味着我们可以用一颗模板树维护一下d[y]−2cnt(x,y)d[y]-2cnt(x,y),然后用dfs去枚举x

然后可以发现对于x的一条非树边我们要把y到根节点的路径上所有点的权值都减去2

然后对于点x优先dfs他的重儿子再从重儿子那里继承线段树

也就是说我们对于一条重链只开了1个线段树,而只有log线段树

然后轻儿子的线段树可以开垃圾桶回收靠

空间复杂度就不是两个log了!

但是能写出来是不可能的了

所以我们可以dsuontree

喜提3个log解决了,但是您认为3个log难看?全局平衡二叉树解决了

C

回文浓度小于$$\sum_{C(cnt_i+1,2)}$$

所以直接排序就是最优的!

cnt_i表示由几种数他的总数为i

cnt_a==cnt_b->abababab,babababababa

cnt_a==cnt_b+1->ababa

cnt_a==2可以作为左右括号抱起来!

除此之外没有任何回文方法了!可以打表验证一下,对于所有满足条件的方案有多少混合方式!

出现次数为2的数可以作为左右括号把别人抱起来的

对于2最后我们再去合并

对于ababab,这个外面不能被抱

而本身是回文的就是aaa,ababa可以抱

f[A][B]表示由A个不可套段,B个可套段方案数

然后还是要记录一下这类长度剩下几个,cnt_a的数剩下几个

对于cnt_a==2的数,可以作为左右括号去套可套段,也可以去套空气

ccbb

所以肯定可以枚举这两种选择分别有几种数,然后再去枚举一共套了几段空气

最后我们用一些组合计数去算答案

就解决了!

Powered by Gridea RSS