20zr暑期AB班十连测day7

每个点求第k小的路径长,保证树随机

二分+线段树+树上爬

我们考虑对于一个LCA是不是存在大于二分值的路径K条

发现这个可以对于一个唯一的u建立线段树存子树

然后就可以用点分树的思想 $Olog^3n$

然后发现我们可以换种思路,就是使得点x所有的距离都记录到线段树里

但你发现直接做不太好

dep[u]+dep[i]-2dep[LCA]<=ans

也就意味着我们可以用一个线段树维护 $dep[i]-2dep[LCA]$

然后我们depi显然不变,但2deplca随着x走可能会发生改变,因为lca可能会发生改变

x子树外的i他们的lca显然不会变,然后你会发现只有对于x子树里那些i他们的lca会变为x下面的点...所以只需要每走一步做一个简单的子树全部修改操作即可

然后查询就是一个树状数组二分,您会发现树状数组在开2的次幂时正好是和二分时的mid一样的

看code


#include<iostream>
#include<cstdio>
#include<cstring>
#define R register
const int MAXN = 5e5 + 7;
using std::max;
int n, K;
int dfn[MAXN], dep, dp[MAXN], dfm[MAXN], topE[MAXN], ans[MAXN];
int ccnt, len[MAXN], home[MAXN], nxt[MAXN], to[MAXN];
inline void ct(int x, int y, int z) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
	len[ccnt] = z;
}

namespace fastIO {
#define BUF_SIZE (1<<19)
	static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = buf + BUF_SIZE;
	inline char nc() {
		if(p1 == pend) {
			p1 = buf;
			pend = buf + fread(buf, 1, BUF_SIZE, stdin);
		}
		return *p1++;
	}
	inline int read() {
		char s = 0;
		int x = 0;
		for(; !isdigit(s); s = nc());
		for(; isdigit(s); s = nc())x = (x << 1) + (x << 3) + s - '0';
		return x;
	}
	int _C = -1, _Z;
	char _sr[1 << 21], _z[20];
	inline void Ot() {
		fwrite(_sr, 1, _C + 1, stdout), _C = -1;
	}
	inline void print(int x, char s) {
		if(_C > 1 << 20)Ot();
		while(_z[++_Z] = x % 10 + 48, x /= 10);
		while(_sr[++_C] = _z[_Z], --_Z);
		_sr[++_C] = s;
	}
}
using namespace fastIO;

const int MAXM = (1 << 20) + 1;
namespace  BIT {
	int sum[MAXM];
#define lowbit(x) (x&-x)
	inline void add(int x, int y) {
		for(; x < MAXM; x += lowbit(x))sum[x] += y;
	}
	inline int query() {
		R int l = 0, r = MAXM - 1, s = K;
		while(l + 1 != r) {
			int mid = (l + r) / 2;
			if(sum[mid] >= s)r = mid;
			else s -= sum[mid], l = mid;
		}
		return l + 1;
	}
}
using namespace BIT;

int nwdp[MAXN], mdp;

inline void dfs(int u, int F) {
	dfn[u] = ++dep;
	mdp = max(mdp, dp[u]);
	for(R int i = home[u], v; i; i = nxt[i]) {
		v = to[i];
		if(v == F)continue;
		topE[v] = len[i];
		dp[v] = dp[u] + len[i];
		dfs(v, u);
	}
	dfm[u] = dep;
}

inline void dfs1(int u, int F) {
	if(u != 1)
		for(R int i = dfn[u]; i <= dfm[u]; ++i) {
			add(nwdp[i], -1);
			nwdp[i] -= 2 * topE[u];
			add(nwdp[i], 1);
		}
	ans[u] = dp[u] + query() - mdp;
	//-mdp是为了防止负数
	for(R int i = home[u], v; i; i = nxt[i]) {
		v = to[i];
		if(v == F)continue;
		dfs1(v, u);
	}
	if(u != 1) {
		for(R int i = dfn[u]; i <= dfm[u]; ++i) {
			add(nwdp[i], -1);
			nwdp[i] += 2 * topE[u];
			add(nwdp[i], 1);
		}
	}
}

int main() {
	n = read();
	K = read();
	for(R int i = 1, x, y, z; i < n; ++i) {
		x = read();
		y = read();
		z = read();
		ct(x, y, z);
		ct(y, x, z);
	}
	dfs(1, 0);
	++mdp;
	for(R int i = 1; i <= n; ++i) {
		nwdp[dfn[i]] = dp[i] + mdp;
		add(nwdp[dfn[i]], 1);
	}
	dfs1(1, 0);
	for(R int i = 1; i <= n; ++i)print(ans[i], '\n');
	Ot();
	return 0;
}

dp[x][k][0/1]表示x的子树access了k次后不同的子树形态,x到他儿子的边中有没有实边

然后考虑合并

但是你会发现子树之间的access顺序会决定不同的树的形态

所以我们可以钦定那条边是实边,然后考虑其他的就顺序任意即可,而钦定的放在最后access

您发现我们不需要考虑access具体操作顺序,只需要知道这个是最后的

无效操作?意义不大,我们统计答案的时候搞一下就行了

代码中g就是对应了0那一维,f对应了1

code


#include<iostream>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define R register
using namespace std;
const int P = 998244353;
const int MAXN = 1e4 + 7;
const int MAXM = 5e4 + 7;
int siz[MAXN], n, m, k, a[MAXN], f[MAXN][520], g[MAXN][520];
int to[MAXM], nxt[MAXM], home[MAXM], ccnt;

inline void ct(const int &x, const int &y) {
	ccnt++;
	nxt[ccnt] = home[x];
	to[ccnt] = y;
	home[x] = ccnt;
}

inline void dfs(const int &u, const int &F) {
	f[u][0] = 1;
	for(R int i = home[u], v; i; i = nxt[i]) {
		v = to[i];
		if(v == F)continue;
		dfs(v, u);
		for(R int j = siz[u]; j >= 0; --j) {
			g[u][j + 1] = (g[u][j + 1] + f[u][j]) % P;
			//g,f相互转移
			for(R int k = 0; k + j <= m && k <= siz[v]; ++k) {//限制次数上限,sizv,m
				if(g[v][k]) { //如果不是空
					g[u][j + k] = (g[u][j + k] + 1ll * f[u][j] * g[v][k]) % P;
					//f是考虑access的,所以可以从f向之后g更新
					g[u][j + k] = (g[u][j + k] + 1ll * g[u][j] * g[v][k]) % P;
					//直接乘即可,g是任意的?
					f[u][j + k] = (f[u][j + k] + 1ll * f[u][j] * g[v][k]) % P;
					//都可以这样更新
				}
			}
		}
		siz[u] += siz[v];
		siz[u] = min(siz[u], m);
	}
	for(R int i = 1; i <= siz[u]; ++i) {
		g[u][i + 1] = (g[u][i + 1] + f[u][i]) % P;
		//可以认为我们能多access一次然后不access的都不考虑了
	}
	siz[u] = siz[u] + 1;
	siz[u] = min(siz[u], m);
	//大于就价值不大
}

int main() {
	scanf("%d%d", &n, &m);
	for(R int i = 1, x, y; i < n; ++i) {
		scanf("%d%d", &x, &y);
		ct(x, y);
		ct(y, x);
	}
	dfs(1, 0);
	int ans = 1;
	for(R int i = 1; i <= m; ++i)ans = (ans + g[1][i]) % P;
	//g是DP数组,表示我们access几次
	printf("%d\n", ans);
	return 0;
}

考虑对于每一位1算出他的方案数

然后 $f[i][j][k]$ 表示有几对数满足 $|a_{i}-a_{3+i}|=x$ 且 $a_i xor a_i+3$

而且我们可以枚举绝对值符号的正负性

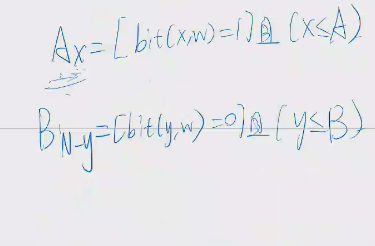
然后会发现是一个卷积,优化一下就是blog^2b的

i^(i+x)第w位的值是有i在第w位的值和i+x在第w位的值

(i+x)在o~w-1时是否进位 $i%2^w+x%2^w>2^w$

然后就可以枚举一下

bit(i,w)=0,bit(x,w)=0,那么i+x必须要进位所以i%2^w>=2w-x%2^w

从而计算出x在哪个范围里...就可以发现我们的i和i+w了

本质上是一个数位dp,但是我们可以通过钦定一个然后直接计数

虞皓翔大佬的解法

夏晓光(loveJY)的博客

20zr暑期AB班十连测day6