夏晓光(loveJY)的博客

仍要向下扎根,向上结果

首页 归档 标签 关于 友链

20zr暑期AB班十连测day8

2020-08-04 14 min read # 主席树 # 二进制 # 动态规划

A

传统的博弈论,k-nim模型,对于k-nim模型他的SG值显然还是石子个数

而是否决胜是对于每一个二进制位求和能不能被k+1整除

然后就是统计有多少种方案使他们最后是0

这样我们就可以DP啦QwQ

三进制xor就是每一位加起来%3

那么我们是数位DP,从高向低去确定每一位,所以我们要记下是否卡到上/下界

然后这是三种状态,压一压就是3^n种状态,一共有log位,每一位记为w

每次转移时可以枚举a1~n第w位值是什么

就可以做到O(6^nlog)

显然可以优化转移变为一个个枚举

那么我们就再记两维表示我们已经转移了前i个数的他们的w一位的和

f[S][w][i][sum]表示所有a的w上面的位,a1...ia_{1...i}的第w已经定好了

sum表示a1...wa_{1...w}在第w为的值

然后这样子就能做到像插头dp一样转移

三进制处理?

预处理每个3的i次是什么,然后(x/3^i)%3就是某个数x三进制下第i位是几

然后code:


#include<cstdio>
#include<cstring>
#include<iostream>
#define pii pair<int,int>
#define fi first
#define se second
#define mkp(x,y) (make_pair(x,y))
using namespace std;
const int P = 998244353;
const int MAXN = 14;
const int MAXM = 6e5 + 7;
int n, l[MAXN], r[MAXN];
int f[2][MAXM][3];
int p3[MAXN];
#define BIT(x,i) ((x)/p3[(i)]%3)//qwq

int trans(int w, int L, int R, int o, int e) {
	//w就是那一位
	//L是我们这个数的下界
	//R是上界
	//O是S的第i-1位
	//e是当前的我们想要加上的数
	int tmp = (L / (1 << (w + 1))) == (R / (1 << (w + 1)));
	//L是否在这一位是等于R的
	int eqL = (o == 0);
	//如果为0表示我们卡下界
	int eqR = (o == 1) | (o == 0 && tmp);
	//为1我们卡上界
	//或者卡下界,下界==上界
	int wL = (L >> w) & 1;
	//wL是表示L第w是否为1
	int wR = (R >> w) & 1;
	//...
	if(eqL && e < wL)return -1;
	//eqL表示卡了下界,我们没法凑出
	if(eqR && e > wR)return -1;
	//这个是卡了上界
	eqL &= (e == wL);
	eqR &= (e == wR);
	//如果我们完全卡下界就没了
	//只能返回0
	if(eqL)return 0;
	//否则我们返回3^下的那个,相当于异或成功了
	return 2 - eqR;
}

int main() {
	scanf("%d", &n);
	p3[0] = 1;
	for(int i = 1; i <= n; ++i)
		p3[i] = p3[i - 1] * 3;
	for(int i = 1; i <= n; ++i)
		scanf("%d%d", &l[i], &r[i]);
	memset(f, 0, sizeof(f));
	int nw = 0;
	f[nw][0][0] = 1;
	for(int bit = 29; bit >= 0; --bit) {
		//枚举每个数位
		//显然这货被我们滚掉了
		//因为他只是可行性判断的一部分
		for(int i = 1; i <= n; ++i) {
			//枚举我们去确定的前i位
			memset(f[nw ^ 1], 0, sizeof(f[nw ^ 1]));
			for(int S = 0; S <= p3[n] - 1; ++S) {
				//枚举所有已经定好的w上面的位
				for(int v3 = 0; v3 <= 2; ++v3) {
					//枚举所有可能的w和
					if(f[nw][S][v3]) {
						int w = f[nw][S][v3];
						for(int v = 0; v <= 1; ++v) {
							//枚举我这位是0还是1
							if(i == n && ((v3 + v) % 3 != 0))continue;
							int nv = trans(bit, l[i], r[i], BIT(S, i - 1), v);
							//trans出新nv
							if(nv == -1)continue;
							int nS = S - p3[i - 1] * BIT(S, i - 1) + p3[i - 1] * nv;
							//计算S的变化
							//就是减去原来的i-1位然后加上新的i-1位
							//是三进制下的
							f[nw ^ 1][nS][(v3 + v) % 3] = (f[nw ^ 1][nS][(v3 + v) % 3] + w) % P;
						}
					}
				}
			}
			nw ^= 1;
		}
	}
	long long ans = 0;
	for(int i = 0; i < p3[n]; ++i)
		ans = (ans + f[nw][i][0]) % P;
	//当最后为0时,也是一切尘埃落定之时
	printf("%lld\n", ans);
	return 0;
}

B

首先我们发现去重是个有毒的东西,所以我们可以考虑转为数组下标的数组

然后钦定对于一个b,对应其字典序最小的S这样就不会算重

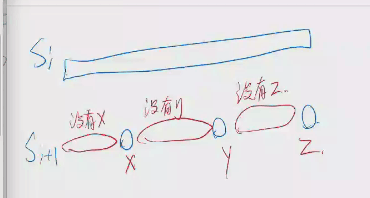
然后怎么算Si+1是字典序最小的那个呢?

首先对于s_i+1要满足xy中没有y,yz中没有z.....

然后如果没有任何一个存在的情况就是字典序最小的qwq

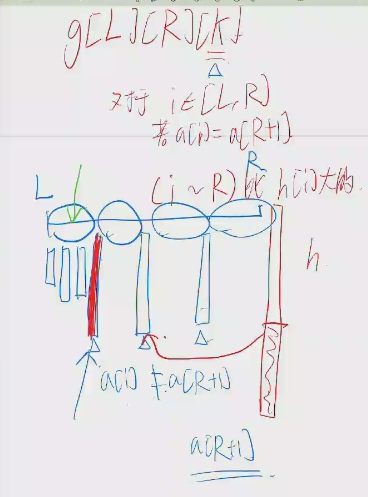
h_i是最大的D,满足i \in S_D

求几个合法的h就是求几个合法的树状图...

显然我们对于i<j,a_i==a_j,弱h_j>h_i,则就由于被挡住而存在k在i,j之间h_k>h_i

不然考虑S_k+1可以把j替换为i

然后考虑这个限制,g[L][R][K]表示对于L~R所有i,若a_i=a_R+1

那么L~R一定有一个比h_i大的

首先我们可以枚举有哪些h_i=k

首先不能等于a_R+1否则我们会发生平移操作

枚举完之后又会分成若干个子区间啦

第一个转移时被保护的

f是没有R+1的限制下的方案数

R+1的限制就是对于一个a_i=a_R+1,中间一定要有一个h_i帮他挡着

因为我们区间是在一点点定值下去的...

如果随便定会使得不满足i~R+1的限制,所以只能在某个地方才能定值

我们定值的过程相当于定K的位置,就是说从大到小去定每个h的值

然后我们g有限制的就要转移时不能给a_i=a_r+1先定值

而f则可以通过g数组在我们定好值的位置上加上限制来转移

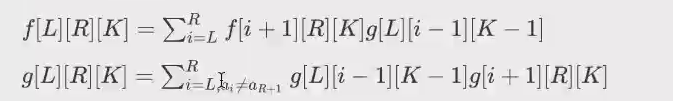
K=3

枚举i=1~n,记一下S2和S3上一步是什么....

最后说实话讲的有点乱

其实就是a_i==a_j,i<ji<j,那么i一定出现在j前面的S里,也就是说只有两个都选上时的序列才行

然后这个是限制,求一下本质不同的h序列个数

code:


//From Ultimate Destroy
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int MAXN = 111;
const int P = 998244353;

int n, a[MAXN], K, g[MAXN][MAXN][MAXN], f[MAXN][MAXN][MAXN];
//妈的讲的和实际上是反的
inline void init() {
	int flg = 0;
	//初始化部分
	for(int i = 1; i <= n; ++i) {
		for(int j = i; j <= n; ++j) {
			f[1][i][j] = 1;
			//这显然只有一种方案
			if(j < n) {
				//对于小于n的情况
				//如果定他大于n会与这个dp状态不太符合
				flg = 0;
				for(int k = i; k <= j; ++k) {
					//枚举
					if(a[k] == a[j + 1])flg = 1;
					//如果满足这两个相等,那么就是说这之前的才行!
					//也就是这个区间会被卡r+1啊
				}
				if(!flg)g[1][i][j] = 1;
			}
		}
	}
}

inline void dp() {

	for(int k = 2; k <= K; ++k) {
		for(int L = 1; L <= n; ++L) {
			for(int l = 1; l <= n - L + 1; ++l) {
				int r = l + L - 1;
				int w = f[k - 1][l][r] * (L != n);
				//如果L是n长度就太长了
				//显然就成了个初始态
				for(int p = l; p <= r; ++p) {
					int t = 1;
					//枚举转折点
					if(p < r)t = t * 1ll * f[k][p + 1][r] % P;
					//如果不是右端点,我们可以乘上之后那段区间随意的方案数
					if(p > l)t = t * 1ll * g[k - 1][l][p - 1] % P;
					//但是前面那段区间是受到限制的
					//不能放k-1
					w = (w + t) % P;
				}
				f[k][l][r] = w;

				if(r < n) {
					//r+1<=n
					w = g[k - 1][l][r] * (L != n);
					for(int p = l; p <= r; ++p)
						if(a[p] != a[r + 1]) {
							//我彪掉了...
							//这个a_p显然只能先定值k啊!!!
							int t = 1;
							if(p < r)t = t * 1ll * g[k][p + 1][r] % P;
							//显然由于本身我们更新的缘故,这个东西就要受到限制
							if(p > l)t = t * 1ll * g[k - 1][l][p - 1] % P;
							//然后又要受到新限制啦qwq
							w = (w + t) % P;
							//这是那个西格玛
						}
					g[k][l][r] = w;
				}
			}
		}
	}
}


int main() {
	scanf("%d%d", &n, &K);
	for(int i = 1; i <= n; ++i) {
		scanf("%d", &a[i]);
	}
	init();
	dp();
	printf("%d\n", f[K][1][n]);//QAQ
	return 0;
}

C

Q=1的暴力

首先二分答案S

统计一下最多选多少个数

首先小于S/2一定被选

而>S/2的两个区间内肯定只能选一个数,所以可以枚举每个区间看最小值能不能选,能选答案+1

多次询问就用个数据结构维护一下,对于小于S/2的个数可以主席树

但是第二个统计有点毒啊...

于是我们思考有多少个三元组(x,y,z)满足L<x<z<y<RL<x<z<y<R

然后a[x],a[y]<S/2a[x],a[y]<S/2

然后a[k]a[k]是[x+1,y−1][x+1,y-1]最小值

而且a[k]>S/2a[k]>S/2否则会跨两个区间

a[k]+max(a[x],a[y])<=Sa[k]+max(a[x],a[y])<=S

观察第2,3,4,三个条件我们可以发现对于一个k有唯一的一组x,y能与之对应

那么对于一个三元组k,有两个限制,值域限制和位置限制

首先我们可以算出s的范围

S∈[a[k]+max(a[x],a[y]),2a[k])S \in [a[k]+max(a[x],a[y]),2a[k])

那么显然我们一个k就是一个区间加,然后S是单点查

当然也可以k单点加(差分)S区间查,可主席树

然后这是三维数点

显然我们可以找到对于L,R中左边第一个dL,右边第一个dR满足小于等于S/2的

那么满足条件的三元组都在这个区间里面而且也一定都在这个区间里面

所以就变成了k在dL,dR之间,就变成了了二维数点

实际上我们要找小于的,否则可能会因为相等的值而找重复了,实测这也是对的

这样就可以二分+树状数组两个log解决了

minmax卷积 : a_i+j=min(max(b_i,c_j))

首先我们考场上有一个类似笛卡尔树的堆的做法

就是考虑一开始都选上,然后我们删去相邻最大和的,就一直删下去知道满足了

code:


#include<iostream>
#include<cstdio>
#include<cstring>
#include<set>
#define se second
#define fi first
#define mkp(x,y) (make_pair(x,y))
#define ins insert
using namespace std;
const int MAXN = 1e5 + 7;
multiset<pair<int, pair<int, int> > > st;
int nxt[MAXN], pre[MAXN], a[MAXN], n, Q, vis[MAXN];

inline void del(int x) {
	nxt[pre[x]] = nxt[x];
	pre[nxt[x]] = pre[x];
}

inline void solve(int l, int r, int z) {
	for(int i = l; i < r; ++i) {
		st.ins(mkp(a[i] + a[i + 1], mkp(i, i + 1)));
		// printf("%d\n", a[i] + a[i + 1]);
		// printf("%d?\n", st.size());
		nxt[i] = i + 1;
		pre[i] = i - 1;
	}
	pre[l] = r;
	st.ins(mkp(a[r] + a[l], mkp(r, l)));
	nxt[r] = l;
	pre[r] = r - 1;
	int k1, k2;
	// printf("%d?\n", st.size());
	while(st.size() > z) {
		auto it = st.end();
		--it;
		int u = (*it).se.fi;
		int v = (*it).se.se;
		// printf("%d?%d %d\n", u, v, (*it).fi);
		if(vis[u] && vis[v]) {
			st.erase(it);
			continue;
		}
		if(vis[u] || (a[u] < a[v] && !vis[v]))u = v;
		// printf("%d?\n", u);
		//我们只删除u
		k1 = a[u] + a[nxt[u]];
		k2 = a[u] + a[pre[u]];
		vis[u] = 1;
		st.erase(it);
		if(u != v)st.erase(st.find(mkp(k2, mkp(pre[u], u))));
		else st.erase(st.find(mkp(k1, mkp(u, nxt[u]))));
		del(u);
		st.ins(mkp(a[pre[u]] + a[nxt[u]], mkp(pre[u], nxt[u])));
	}
	auto it = st.end();
	--it;
	printf("%d\n", (*it).fi);
	st.clear();
	return;
}

int main() {
	// freopen("test.in", "r", stdin);
	// freopen("test.out", "w", stdout);
	scanf("%d%d", &n, &Q);
	for(int i = 1; i <= n; ++i)scanf("%d", &a[i]);
	if(n <= 10000 || Q <= 10000) {
		for(int i = 1, x, y, z; i <= Q; ++i) {
			scanf("%d%d%d", &x, &y, &z);
			for(int i = x; i <= y; ++i)vis[i] = 0;
			solve(x, y, z);
		}
	}
	return 0;
}
Powered by Gridea RSS