A. 【21省选第一轮集训】基础

并查集dijkstra做法

首先对于点u,我们所有转移的边出去的权一定是$dis_u+a_u$

也就是都是一样的,也就是说我们这个转移是可以直接放入堆里增广的

那么我们会发现,取出来一个转移x,就会对于x能够转移到的区间内的决策点全部更新,他们就是直接成为了最短路啊

然后这样做我们要只把区间内没有经过的点拿出来,把他们的最优转移放入堆里面就好了...

所以说我们就能用一个并查集,维护那些点已经访问过了,对于指向自己的是没有访问过的,对于这个区间转移,每次从左端点向后跳,然后跳到每个根直接把它转移了就好

李队做法

我们考虑一个路径向回走太多一定不会更优,就是从第一行的x位置,走到一个$x-y(y>k)$,然后再从这个位置走回x一定不会更优

所以我们不需要考虑这个下界,所以可以发现我们可以

每个点向这个点+k位置连边,边权为出点,然后第一排的点向后一个点连边,然后第二排点向前一个点连边,边权为某个点减去某个点

就是

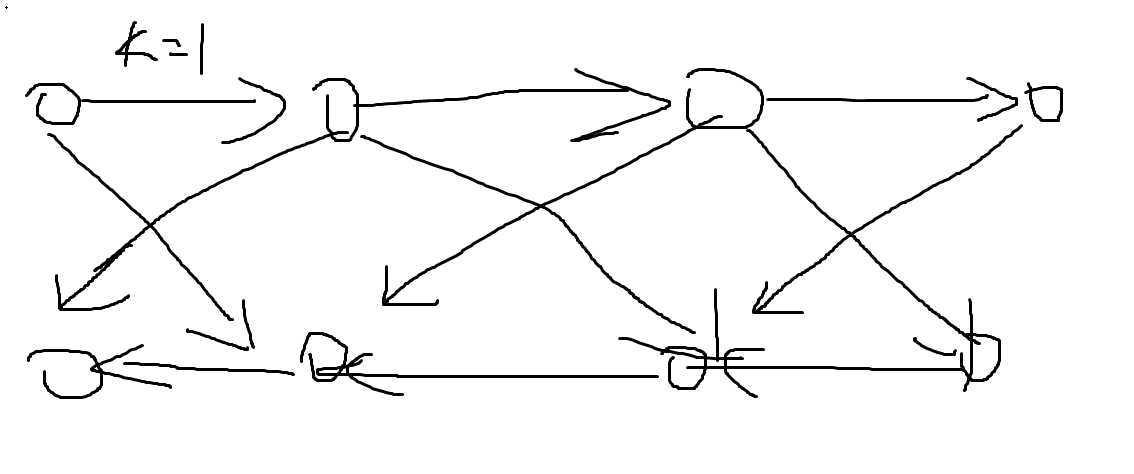
B. 【21省选第一轮集训】数据结构

我们有一个很简单的暴力想法,就是对于所有已有的修改来维护答案

比如插入一个y或者x,相当于对于一个点坐标向后移动,一个之前插入的向后移动,同时对于之前插入的操作,假设有一行或者一列覆盖到了这个位置,相应的就会对于这一列产生一个横坐标或者纵坐标推平类的影响,同时这个推平类影响之后所有影响是我们需要知道的东西

不难发现直接maintain是$O(Q^2)$

第一种做法是可持久化平衡树

直 接 做

首先对于前i个操作建立平衡树,然后对于第i次操作,他的影响是所有编号大于他的操作都会被+1,然后加入到集合中

对于区间加,可以使用可持久化标记,即我们对于这次修改新建立的叶子点直接上去即可

然后对于插入,直接新建节点即可

然后我们接下来考虑怎么实现查询有没有覆盖到他的

可以直接单点查询这个值

然后考虑怎么实现这个操作之后的有多少个能够对于他产生影响

我们可持久化就是搞这个的/cy

你考虑只有序列在这个区间内,然后前k个操作能够使之变小和前i个操作能使之变小的

但是说你会发现此时我们要的信息是前k个中当前位置在x之后的操作

但是他们的相对顺序不可能变

所以只需要直接二分,然后在原树上查询,就是$polylog$的qwq

这个可持久化不够阳间啊QAQ

考虑能不能只按照标号维护一个东西啊?然后让两个log变成一个log啊

相当于一个平衡树,每次插入一个数,然后每次后继加个1

可以用重量平衡树维护,因为重量平衡树不需要翻转,所以我们可以用节点x,表示编号为(l,r)实数编号区间,然后这个点的编号就是mid

然后我们查询直接访问树上这个节点对应编号即可

修改时插入这个节点一路改到根上

然后我们如果不平衡就重构一下就能$O(logn)-O(1)$了!

所以两个log就被马耀华爷爷搞成1个log了!

然后我们还有官方做法

我们现在缺点在于在线QAQ

离线可以线段树分治,所以在线我们可以考虑二进制分组

储存前面所有的询问,并且将他们二进制分组,当一组正好满$2^k$的时候,我们利用归并排序将他O(n)重构,否则视为不存在

然后最后我们会有一个两个的零散快,他们是可以直接暴力维护顺序的qwq

然后我们从最后一个块向前不停的用二分查找第一个覆盖他的操作

但是有一个问题,我们无法知道实际上被其余操作影响的那些操作的标号/jk

不难发现我们在建立这一个区间的时候可以直接处理出区间中这些操作对于区间内操作的影响,就是前后左右移动移动类似的,也是归并排序就可以解决

但是说我们不能保证的是分开的两端之间的答案相互影响qaq

所以此时我们需要利用题目的性质,就是影响很具有可减性,在回退操作时前面插入一个数使得操作后移了,等价于x向前移动了,所以直接让x,y对应的坐标减少即可

可以证明这个转化是等价的

首先对于原来的答案x,x之后的任意操作,他们一定最后会在询问的后方

那么他们什么时候会在询问的后方,而不至于对于询问产生影响呢?

你会发现要么是在x减少的时候,x跳到这个操作之前了

否则,说明是他同一块内的操作淦死了他,这个情况我们再生成这个块的时候,就把标号重新分配好了

所以就对了

复杂度$O(nlog^2n)$

可删除线性基

如果我们要删除一个x

考虑所有b,表示哪些异或出来的,然后我们有这个$b_{j,x}$为1