讲生成函数先学

麦克劳林级数

麦克劳林级数是函数在x=0处的泰勒展开

泰勒展开是

$f_x=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+...+\frac{f^{(n)}(0)}{n!}x^n$

即我们带入x=0得到的值就是麦克劳林级数的系数

$\frac{1}{1-x}=1+x+x^2+x^3+....+x^n=\sum_{i=0}^n x^i$

证明:

显然有带入0时常数项为1

分数求导的规则是

（分子的导数分母-分子分母的导数）/分母的平方。

即(u/v)' = (u'v-uv')/v²。

一阶导数为$\frac{1}{(1-x)^2}$

故我们有带入x=0,得到1

同理,对于一阶导数再求导

$(\frac{1}{(1-x)^2})'=\frac{-((1-x)^2)'}{(1-x)^4}=\frac{-(2x-2)}{(1-x)^4}=\frac{2}{(1-x)^3}$

和1/2!抵消

继续求导?我们其实可以观察发现下一步得到分母会倍增为6,然后分子会放下一个3,留下一个2

就是:$\frac{6(1-x)^2}{(1-x)^6}$

然后你会发现每次分母会+1,并且把分子上多乘上一个数,就正好和系数消掉了

记忆方式:是不是和等比数列求和一模一样?

$\frac{1}{1+x}=1-x+x^2-x^3+....+x^n=\sum_{i=0}^n (-1)^ix^i$

一阶导数为$\frac{-1}{(1+x)}$

和上式不同的是,因为上式有个分母求导那个系数是负的,然后又有个负号变回来,而这个因为减法的符号变不回来,所以每求一次导都会变一次号

其他的系数和上述过程相同

记忆方式:是不是把上式的x变为-x再等比数列求和?

$e^x=1+x+\frac{x^2}{2!}+..+\frac{x^n}{n!}$

有个结论$(e^x)^{(n)}=e^x$,这使得e函数有无与伦比的增长率,也使得他在x=0的时候就是个1菜鸡

$sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}....=\sum_{n=0}^{\inf}(-1)^n\frac{x^{2n+1}}{(2n+1)!}$

为什么?因为

$\frac{\pi}{4}=1-1/3+1/5-1/7...$

cos刚好相反是所有偶数的阶乘,也有$-1^n$

$ln(x+1)=x-\frac{x^2}{2}+\frac{x^3}{3}....$

挺好记的,但是没用吧

$\frac{1}{1-ax}=1+ax+a^2x^2+a^3x^3+.....+a^nx^n$

一阶导数是

$\frac{a}{(1-ax)^2}$

我觉得看了上面的你已经知道接下来会长成什么样子了

麦克劳伦结束了

表示序列的一种有效方法就是生成函数，它把序列的项作为一个形式幂级数中变量 [x] 的幂的系数。

OGF

$a_1,a_2...a_n$的普通生成函数是

$G(x)=a_0+a_1x+a_2x^2+....+a_nx^n=\sum_{i=0}^n a_k x^k$

定理:

生成函数乘法等价于幂级数的多项式卷积,生成函数的加法等价于幂级数多项式加法

eg:

$\frac{1}{(1-x)^2}=(1+x+x^2....)(1+x+x^2....)=1+2x+3x^2+4x^3.....$

证明其实很简单,你会发现这个$\frac{1}{(1-x)^2}$正好是我们$\frac{1}{x-1}$一阶导数的值,于是我们继续求导会发现我们求导的结果比阶乘多一个n ,快一步qwq

广义二项式定理

$|x|<1$收敛

$(1+x)^u=\sum_{k=0}^{\inf}\binom{u}{k}x^k$

$(x+y)^u=\sum_{k=0}^{\inf}\binom{u}{k}x^{u-k}y^k$

其中甚至用到了广义组合数,谁爱证明谁证

完蛋了然后就是应用

$(1-x)^{-n}=\sum_{k=0}^{\inf}\binom{n+k-1}{k}x^k$

于是我们的EI哥哥教教了广义组合数

$\binom{m}{n}=\frac{\prod_{i=n-m+1}^n i}{m!}$

于是我们观察一下,当k是奇数的时候,我们组合数展开后有一个负号,但同时后面那一项次方也有个负号,抵消了

当k是奇数的时候,二者都不会有负号

$(1-x)^{-n}=\frac{(-n)*(-n-1)*(-n-2)..*(-n-k-1))}{k!}=\frac{n*(n-1)*.....*(n+k-1)}{k!}=\frac{(n+k-1)}{(n-1)!k!}$

故证毕

还有一个....

$\frac{1}{1-x^k}=\sum_{i=0}^{\inf}x^{ik}$

这个真的没法证明,我们感性理解一下为什么吧

取k=2

一阶导数$\frac{2x}{(1-x^2)^2}$

发现....这玩意x=0时是0??

好像明白了什么....再求导一次

$\frac{2+6x^2}{(1-x^2)^3}$

首先根据分母的形式我们能知道常数项应该是阶乘递增没跑了

但是这个接下来就很鬼畜:他会每k次才有一个值非0......

也就是说他产生的原因是把好多项都变成0了,不是什么乘上次方!!

eg:

$h_0,h_1.....h_n$,$h_n$表示$e_1+...+e_k=n$非负整数解个数

根据隔板法这个答案是$\binom{n+k-1}{k}$

然鹅实际上,我们把次方看做值,然后用k个幂级数卷起来也是这个

具体的

$(\frac{1}{1-x})^n=之前那个式子$

P2000 拯救世界

靠,直接构建生成函数,然后多项式乘法卷起来就行了

难度在于NTT,所以是紫

和zhq卷1e5个小时一样简单(

生成函数解决递推式的简单形式

我直接加强例题,求下面递推式的通项公式

$a_x=3a_{x-1}+2,a_0=2$

首先我们有$G(x)=\sum_{k=0}^{\infty}a_kx^k$

$xG(x)=\sum_{k=0}^{\infty}a_k x^{k+1}$

$xG(x)=\sum_{k=1}^{\infty}a_{k-1} x^{k}$

$G(x)-3xG(x)=a_0+\sum_{k=1}^{\infty}(a_k-a_{k-1}) x^{k}$

$G(x)-3xG(x)=2+2*\sum_{k=1}^{\infty} x^{k}$

$(1-3x)G(x)=2*\frac{1}{x-1}$

$G(x)=\frac{2}{(x-1)(1-3x)}$

喵喵喵接下来:

求解$a_n=a_{n-1}*8+10^{n-1},a_1=9$

不难发现$a_0=1$

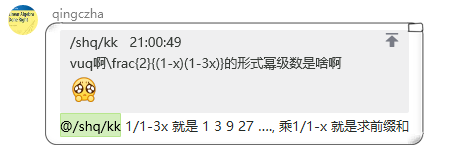
根据上次的通法:

$G(x)-8xG(x)=\sum_{i=1}^{\infty}x^i10^{i-1} + 1$

坏了,这个$10^{i-1}$要出大问题,怎么办?

同时乘10?好像能得到一个萎掉的式子

$G(x)=\frac{9-90x}{10*(1-10x)(1-8x)}$

说不定是对的

然鹅正确处理方式是提出x

$G(x)-8xG(x)=\sum_{i=1}^{\infty}x^{i-1}10^{i-1} + 1$

$G(x)-8xG(x)=\sum_{i=0}^{\infty}x^{i}10^{i} + 1$

$G(x)=\frac{1-9x}{(1-10x)(1-8x)}$

于是做完啦/se

不对,利用粉兔的方法:

$a(1-10x)+b(1-8x)=(1-9x)$

$a+b=1$

$-10x-8x=-9x$

$a=b=1/2$

故$g(x)=\frac{1}{2}(8^n+10^n)$

例题

BZOJ3027Sweet

有 n 种糖果，每种$m_i$个，至少吃掉a个，至多b个，求吃掉糖果的方案数

$n<=10,m<=1e6$

蒟蒻做法:

其实并不困难,我们的多项式是有限项的,而且是只有n个,同时系数都是1

所以做多项式乘法相当于求前缀和,直接做即可,最后能构造出整个多项式,时间复杂度$O(nm)$

题解:

生成函数是$g(x)=\frac{1-x^{m_i+1}}{1-x}$

非常巧妙,相当于截断了!卷起来卷起来

$(1+x+x^2.....)^n*\prod_{i=1}^n{1-x^{m_i+1}}$

而我们又有隔板法(或者二项式反演),前面的多项式第i项系数为

$\binom{i+n-1}{n-1}$

我们再看后面一个$k*x^y$对于答案的贡献,相当于乘上$[a-y,b-y]$这一段区间的$x^j$系数和

会发现这个系数可以变成差的形式,我们只探讨一个

$k*(\binom{n-1}{n-1}+\binom{n-1+1}{n-1}+\binom{n-1+2}{n-1}....\binom{n-1+a-y}{n-1})$

观察到这个是杨辉三角一列的值,我们可以把它搞成

$k*(\binom{n-1}{n}+\binom{n-1}{n-1})+\binom{n-1+1}{n-1}+\binom{n-1+2}{n-1}....\binom{n-1+a-y}{n-1})$

然后就变成了

$k*(\binom{n+a-y}{n})$

qwq

于是做完了,复杂度优秀到天上$O(n*2^n)$

预处理组合数人没了

zhq做法:

考虑容斥,就是说钦定一些糖果出现次数至少为$m_i+1$

那么我们就有考虑凑齐$<=b$方案数

相当于引入第n+1种糖果,他可以任意选

就是一个可以为空的隔板法了

P3978 [TJOI2015]概率论

首先我们可以设俩数组

g(n)表示n个节点二叉树个数

f(n)表示n个节点二叉树的叶子总数

那么我们有转移

$g(n)=\sum_{i=0}^{n-1}g_{i}g_{n-i-1}$

卡特兰数,就是$\binom{n}{2n}/(n+1)$

根据$g_n$和对称性,我们不难推出f的转移式子

$f(n)=2*\sum_{i=0}^{n-1}g_{n-i-1}*f_i$

于是结论(G是卡特兰数生成函数)

$G(x)=xG(x)^2+1$

$xG(x)=\sum_{i=1}^{\infty}g_{i-1}x^i$

$xG(x)^2=\sum_{i=1}^{\infty}g_{i-1}\sum_{j=0}^{\infty}g_jx^{i+j}$

注意到正好符合我们写出的递推式子:和差一的卷积

但是么得常数项,所以我们要加上1 qwq

根据f的公式和我们推出g的公式可以得到f的生成函数形式

$F(x)=2xF(x)G(x)+x$

其中+x,是因为前面的最低项都是2次项,但显然一个点的时候存在方案为1

根据G(x)的公式我们可以直接解方程得到$G(x)=\frac{1-\sqrt{1-4x}}{2x}$

会带入这个F我们有

$F(x)=x*(1-4x)^{-1/2}$

$(xG(x))'=\frac{1}{\sqrt{1-4x}}=\frac{F(x)}{x}$

这个证明是$xG(x)=\frac{1-\sqrt{1-4x}}{2}$

求导即可得到

xG(x)每一项$xg_nx^n=g_nx^{n+1}$

求导为$(n+1)g_nx^n$

也就是右边的是$f(n+1)x^{n+1}/x=f_{n+1}/x^n$

我们一看有

$f_{n+1}=(n+1)g_n$

$f_{n}=ng_{n-1}$

根据卡特兰数的通项公式,我们带入后

$ans=\frac{n*(n+1)}{2*(2n+1)}$

斐波那契通项公式生成函数求法

怎么说呢,挺eazy的,写完之后才发现....qaq

我们有一些小细节

$x^2F(x)=\sum_{i=2}^{\infty} f_{i-2}x^i$

$xF(x)=\sum_{i=1}^{\infty} f_{i-1}x^i$

$F(x)-xF(x)-x^2F(x)=\sum_{i=2}^{\infty} (f_i-f_{i-1}-f_{i-2})x^i + f_0 + (f_{1}-f_0)x$

根据第一项第二项,我们知道$f_0=0,f_1=1$

于是是

$F(x)=\frac{x}{1-x-x^2}$

我们对于分母因式分解,这里有个好方法,就是解出分母的两个根,然后弄出来

$=\frac{x}{(x-\frac{\sqrt{5}-1}{2})(x-\frac{\sqrt{5}+1}{-2})}$

这个不是熟悉的形式幂级数形式,我们直接乘上俩常数然后得到

$=\frac{x}{(\frac{\sqrt{5}+1}{2}x-1)(\frac{1-\sqrt{5}}{2}x-1)}$

$=\frac{x}{(1-\frac{\sqrt{5}+1}{2}x)(1-\frac{1-\sqrt{5}}{2}x)}$

(那个常数被-1掉了qaq)

熟悉的a,b,我们直接待定系数法

$a(1-\frac{\sqrt{5}+1}{2}x)+b(1-\frac{1-\sqrt{5}}{2}x)=x$

就解决了!

我们解得$a=\frac{-\sqrt{5}}{5},b=\frac{\sqrt{5}}{5}$

所以第n项的答案就是

$\frac{\sqrt{5}}{5}*[(\frac{\sqrt{5}+1}{2})^n-(\frac{1-\sqrt{5}}{2})^n]$

么了!

BZOJ3771. Triple

构建一个多项式$(1+x^{a_1}+x^{a_2}+x^{a_3}..)$

不难发现卷三次,然后位置为i的就代表花费i的代价的方案数...

P4841 [集训队作业2013]城市规划

不妨自己做一下?经典套路啦

提示:构建F(x)表示答案的生成函数,$G(x)$表示随意无向图的方案数生成函数

我们应该有$G(x)=F(x)*G(x)*\binom{i-1}{n-1},G(x)=2^{\binom{2}{n}}$

当然如果你不想求逆也是可以的,我们是有反演基本套路:提出边界项的分治FFT做法

指数生成函数(EGF)

指数生成函数是这样的形式

$G(x)=a_0+a_1x+a_2*\frac{x^2}{2!}+a_3\frac{x^3}{3!}+a_4*\frac{x^4}{4!}....=\sum_{i=0}^{\infty}a_i\frac{x^i}{i!}$

如果您熟悉麦克劳林展开,这东西就是没有把上面系数干掉的生成函数形式~

相对于OGF,他携带了有序这个信息qwq

记住

$e^x=1+x+\frac{x^2}{2!}....=\sum_{i=0}^{\infty}\frac{1}{i!}x^i$

$P^{n}_k$的生成函数?即n个元素的选k个排列数生成函数

挺妙的

$G(x)=1+nx+\frac{n!}{2!(n-2)!}x^2+...+\frac{n!}{n!0!}x^n=(1+x)^n$

八个元素,有3个$a_1$,2个$a_2$,3个$a_3$从中选择6个元素,可能的排列数?(值相同元素本质相同)

考虑构建三个a的EGF,然后卷起来

卷起来之后,我们得到不是一个EGF的形式,再转换成EGF的形式即可

啥意思呢?比如本题中x^4系数为$\frac{35}{12}$,于是我们改写成$\frac{70}{4!}$这样就对劲了,70是选4个元素的排列的方案数

至于怎么改写我也不知道

计算$(\sum_{i=0}^{\infty}r^nt^n/n!)^2*(\sum_{n=0}^{\infty}t^n/n!)^3$

$=e^{3rt}*e^{3t}$

$=e^{(2r+3)*t}$

$=\sum_{n=0}^{\infty}(2r+3)^nt^n/n!$

开始妙起来了

用红蓝绿 3 种颜色去涂 1*n 的棋盘，每格涂一种颜色，求使得被涂成红色和蓝色的方格数均为偶数的的涂色方法数。

有

$(1+\frac{x^2}{2!}+\frac{x^4}{4!}+....)^2*(1+x+\frac{x^2}{2!}+\frac{x^3}{3!}....)$

这个前一项构造一下相当于
$\frac{e^x+e^{-x}}{2}$

$(\frac{e^x+e^{-x}}{2})^2e^x$

$\frac{e^{3x}+2e^x+e^{-x}}{4}$

第n项就是$3^n+2+(-1)^n/4$

n个球放入$A_1,A_2,A_3,A_4$使得$A_1$有奇数个球$A_2$有偶数个球的不同放球方案数

$G(x)=(1+\frac{x^3}{3!}+....)(1+\frac{x^2}{2!}+.....)*(1+x+\frac{x^2}{2!})$

$\frac{e^x-e^{-x}}{2}*\frac{e^x+e^{-x}}{2}*e^{2x}$

$\frac{1}{4}(e^{4x}-1)$

$\sum_{i=0}^{\infty}\frac{4^n}{4}x^n/n!$

$4^{n-1}$就是答案qwq

常用的生成函数

$\frac{e^x-e^{-x}}{2}$

如果乘-1,放到前面吧qwq

$\frac{e^x+e^{-x}}{2}$

我觉得不用说吧qwq

$arcsin(x)=x+\frac{1}{2}*\frac{x^3}{3}+\frac{1*3}{2*4}\frac{x^5}{5}+\frac{1*3*5}{2*4*6}\frac{x^7}{7}$

$arcsin(x)=\frac{1}{\sqrt{1-x^2}}$

可以硬求导证下去

注意EGF的卷积是这样子的:

$F(x)*G(x)=\sum_{i=0}^n(\sum_{j=0}^n\frac{a_j*b_{n-j}}{j!*(n-j)!})\frac{x^n}{n!}=\sum_{i=0}^n(\sum_{j=0}^na_j*b_{n-j}*\binom{n}{j})x^n$

好像根据一些神笔理论我们有

$G(x)=F(x)/1+F^2(x)/2!+F^3(x)/3!+......$

$G(x)=e^{F(x)}$

$F(x)=ln G(x)$

求出G(x)ln一下就有F了

POJ3734

用红黄蓝绿给 n 个有标号的格子染色，要求红色和绿色必须是偶数个，求方案数。对 1e9+7 取模。

有标号问题,EGF卷一下即可

答案是$\frac{4^n+2^{n+1}}{4}$

BZOJ3456 城市规划

可 怕

这个题EGF做法简单的一批...

$G(x)=\sum_{i=0}^n \frac{\binom{i}{2}}{i!}x^i$

显然是n个点无向任意图的EGF

然 后 答 案 就 是 $ln G(x)$ 的 系 数

为什么呢?因为你设出来F(x)表示答案的EGF,然后满足那个形式后正好答案就是对的!.....

F卷F相当于枚举了连通块个数这样子/ll,然后连通块之间没有区别所以除以阶乘

注意实际实现的时候我们EGF乘法并不需要,最后还是要乘上阶乘的qwq

51nod1728 不动点

显然问题可以转换成n个点高度小于等于k的有向森林计数

F(k)为上述答案的生成函数,G(k)为连通的一个有向树的,满足每个高度都不超过k的方案数EGF

然后我们显然根据城市规划的正确性有

$F(x)=e^{G(x)}$

怎么求G(x)呢?我们可以考虑把一车高度小于等于k的森林,通过加上一个父亲作为根连起来,但是我们要枚举那个点的标号,即:

$[x^n]G(k)=n[x^{n-1}]F(k-1)$

注意!!这里的多项式系数是不带那个分母的阶乘的!!

也就是说:$G(k)=xF(k-1)$

这尼玛为什么呢?你会发现我们只吞掉了一个n,但是对于EGF,他的系数是$\frac{a_i}{n!}$

所以说如果我们想要从第i项完整推到第i+1项,不仅要乘上x,还要再乘上i才行!

带入上式可以得

$F(k)=e^{xF(k-1)}$

多项式exp k次,然后就做完了

然后你命没了,TLE吧

Codeforces 891E

不妨设$b_i$表示$a_i$进行了多少次

答案等价于求$\prod_{i=1}^na_i-\prod_{i=1}^n(a_i-b_i)$

这个式子可以由一个类似于差分的过程得出:前一次后面减的等于下一次前面加上的

相当于我们去求后面那个东西的期望,完蛋了

期望的等于总权值*总概率,总概率显然就是$\frac{1}{n^k}$

然后我们发现如果直接把总权值当做$\prod_{i=1}^n(a_i-b_i)$的话就少算许多

因为我们的方案显然是有标号选择的,但是我们这个后面统计的时候是无标号的

所以要乘上一个$\frac{k!}{\prod_{i=1}^nb_i!}$,也就是选择次数的可重全排列这个东西,来防止我们少算答案

同样的可重全排列是因为我们看上去不一样的才算做两种方案

$\frac{k!}{n^k}\prod_{i=1}^n\frac{a_i-b_i}{b_i!}$

于是我们只需要求一个后面的权值

你会发现我们至少要枚举个$b_i$吧

不难发现我们可以考虑生成函数去枚举这个$b_i$

$\prod_{i=1}^n\sum_{j=0}^n\frac{a_i-j}{j!}x^j$

这里其实挺OGF的,但是写出来就变成了EGF了,拆开吧

$\frac{a_i}{j!}x^j-\frac{x*x^{j-1}}{(j-1)!}$

EGF还是不太熟练啊,变成这个

$(a_i-x)e^x$

带上π

$\prod_{i=1}^n(a_i-x)e^x$

$e^{nx}\prod_{i=1}^n(a_i-x)$

后面的暴力展开,然后前面的直接??EGF!

发现我们可以卷积,第i项系数是

$\sum_{i=0}^nc_i\frac{n^{k-i}}{(k-i)!}$

然后E乘上去

$E=\sum_{i=0}^nc_i\frac{\prod_{j=k-i+1}^kj}{n^i}$

所以这样就做完啦

时间复杂度$O(k^2)$

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN = 1e5 + 7;
const int P = 1e9 + 7;
int n, k, a[MAXN];
ll f[MAXN];

inline ll ksm(ll x, ll y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

int main() {
	scanf("%d%d", &n, &k);
	for(int i = 1; i <= n; ++i) {
		scanf("%d", &a[i]);
		if(i == 1) {
			f[0] = a[i];
			f[1] = P - 1;
			continue;
		}
		for(int j = i; j ; --j) {
			f[j] = ((-f[j - 1] + f[j] * a[i] % P) % P + P) % P;
		}
		f[0] = 1ll * f[0] * a[i] % P;
	}
	ll ans = 0;
	for(int i = 0; i <= n; ++i) {
		ll tmp = f[i];
		// printf("%lld\n", f[i]);
		for(int j = k - i + 1; j <= k; ++j) {
			tmp = tmp * j % P;
		}
		tmp = tmp * ksm(ksm(n, i), P - 2) % P;
		// printf("%lld\n", tmp);
		ans += tmp;
		ans %= P;
	}
	printf("%lld\n", (f[0] - ans + P) % P);
	return 0;
}

P5488 差分与前缀和

差分等价于OGF乘上$(1-x)$

差分$10^{2333}$次坏了好像是完蛋了,连多项式都处理不出来

但是说我们只看前n项的系数所以只需要$mod x^n$

但是还是完蛋了,直接多项式快速幂还是TLE啊

坏了,多项式exp好像牛逼的不得了

我们把k对于模数取模,然后原多项式取ln再乘上k再exp回去就好啦qwq

去世了

于是我们可以练习生成函数技巧了

$(1-x)^k$

二项式展开

$\sum_{i=0}^{\infty}\binom{k}{i}(-x)^i(-1)^{k-i}$

$=\sum_{i=0}^{\infty}\binom{k}{i}x^i(-1)^i$

做完了,卷一下即可

$(\frac{1}{1-x})^k$

坏事了,我们要广义二项式定理展开啦

$\sum_{i=0}^n\binom{-k}{i}x^i(-1)^i$

然后根据组合数下降幂形式,我们有

$\sum_{i=0}^n\frac{-k^{\underline{i}}}{i!}x^i(-1)^i$

$\sum_{i=0}^n\frac{(k+i-1)^{\underline{i}}}{i!}x^i(-1)^{2i}$

$\sum_{i=0}^n\binom{i+k-1}{i}x^i$

NTT卷一下就好了....

然后么得了,时间复杂度就是O(nlogn)的

UVA1305 Chocolate

坏了坏了我咋不会啊

这个东西要EGF真坑爹,因为抽取是有顺序的......

有标号EGF哈,我们本质不同时看上去不同啊

考虑我们可以枚举选了几个奇数的几个偶数的然后卷一卷啊,选了m个奇数吧

$\frac{(e^x-e^{-x})^m(e^x-e^{x})^{c-m}}{2^c}$

二项式展开,第n项的系数是

$\frac{\sum_{i=0}^m(-m+2i)^n\binom{m}{i}*\sum_{i=0}^{c-m}(2i-c+m)^n(-1)^{c-m-i}\binom{c-m}{i}}{2^c}$

注意我们选出颜色的组合数没乘进去

直接计算就好,西伯利亚题没模数

CF438E The Child and Binary Tree

我:可以照抄不思考吗?

题:我撕了你/cy

根据动态规划推生成函数也是不错的选择

$f_n$表示权值为n的答案,枚举根节点的权值,然后我们有枚举左右两边的权值大小

即:$f_n=\sum_{x \in S(x)}\sum_{j=0}^nf_jf_{n-j-x}$

根据我们之前的卡特兰数不难得到:$G(x)=\sum_{y in S(y)}x^y$

$F(x)=G(x)F^2(x)+1$

1啊1啊/kk

随便解解方程有个F和G的关系,然后多项式求逆之类的乌拉乌拉一下即可

P4451 [国家集训队]整数的lqp拆分

坏了,我怎么什么式子都推不出来了

想想暴力dp,我们有F(x)表示答案的生成函数,G(x)表示斐波那契数列的生成函数

$F(x)=F(x)*G(x)+1$

$G(x)$根据我们之前的推导应该等于$\frac{x}{1-x-x^2}$

带入展开得到$F(x)=1+\frac{x}{1-2x-x^2}$

剩下的就是一个化简求通项的过程

推这个的时候一定要小 心 翼 翼

$g(n)=\frac{(\sqrt 2 + 1)^n -(1-\sqrt 2) ^n}{2\sqrt 2}$

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 1e5 + 7;
const int P = 1e9 + 7;
const int s2 = 59713600;
char s[MAXN];

inline ll ksm(ll x, ll y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

int main() {
	scanf("%s", s);
	int n = strlen(s);
	ll N = 0;
	for(int i = 0; i < n; ++i) {
		N = N * 10 + s[i] - '0';
		N %= (P - 1);
	}
	if(N == 0 && n == 1) {
		puts("0");
		return 0;
	}
	// printf("%lld ? \n", N);
	printf("%lld\n", (ksm(s2 + 1, N) - ksm(P - s2 + 1, N) + P) % P * ksm(2 * s2 % P, P - 2) % P);
	return 0;
}

P4389 付公主的背包

直接构造函数乘起来就算了吧,有个trick是取ln后做加法,然后加速这个加法的过程

我们有$q(x)=\frac{1}{1-x^v_i}$

于是乎构造ln函数,就是

$g(x)=ln q(x)$

复合函数求导法则有:

$F(g(x))'=F'(g(x))*g(x)'$

$g'(x)=\frac{q'(x)}{q(x)}=q'(x)*(1-x^v)=\sum_{i=0}^{\infty}v*i*x^{vi-1}-\sum_{i=0}^{\infty}v*(i-1)*x^{vi-1}=\sum_{i=0}^{\infty}v*x^{vi-1}$

积分积分回去

$\sum_{i=0}^{\infty}v*1/(vi)x^{vi}$

$\sum_{i=0}^{\infty}1/ix^{vi}$

于是整完了,我们使用调和级数然后多项式exp回去即可