数据结构综合篇章,杂糅了一些没有另起门灶的内容

虚树

"这是一颗仅包含$O(n)$个节点却对LCA关系了如执掌的树"

怎么做呢?

考虑现将所有点按照dfn序排序,又因为虚树中无论有多少点都没有关系,所以我们先将一号点插入虚树中

然后考虑怎么用单调栈去维护虚树的一条"右链"

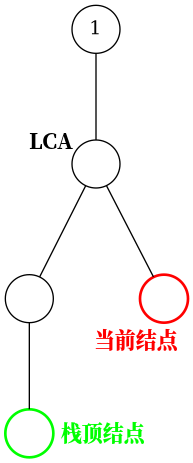
首先,我们单调栈维护的是一个栈顶到栈底的dfn序递减的链,所以先使用栈顶节点和当前点求LCA

如果LCA正好是栈顶节点的话,将当前节点直接入栈

否则,我们考虑不断弹出栈,并建立好一条链,直到栈顶节点的dfn<=当前节点

之后我们获得了栈顶,继续判断刚刚的LCA是不是栈顶节点,如果不是则将LCA和当前节点均入栈

最后我们单调栈只会剩下一条链,直接从栈底到栈顶连边即可!

写的时候还真有细节,就是你会发现有个恶心的例子是

1->2->3(LCA)->5(栈顶)

就是说LCA正好在链上

此时我们5虽然完蛋了,但是他不能和2连边

所以我们每次判断tp-1是否合法

然后再去考虑栈顶元素,如果他的dfn大于LCA(正好是这种情况)就加入一条边

inline void ins(CT x) {
	if(!tp) {
		st[tp = 1] = x;
		return ;
	}
	ance = lca(st[tp], x);
	while((tp > 1) && (dfn[ance] < dfn[st[tp - 1]])) {
		add(st[tp - 1], st[tp]);
		--tp;
	}
	if(dfn[st[tp]] > dfn[ance])add(ance, st[tp--]);
	if((!tp) || (st[tp] != ance))st[++tp] = ance;
	st[++tp] = x;
}

P4565 [CTSC2018]暴力写挂

考虑照抄WC2018通道的做法:对于第一棵树边分治,然后再对于第二棵树建立虚树,在上面跑虚树的dp

$dep_x+dep_y-dep1_{lca}-dep2_{lca}$

这个式子需要给每个点重新附上点权,使得只和x相关一部分,y相关一部分

对于$dep_x+dep_y+dis(x,y)=p_x+p_y+w+dep_x+dep_y$=正好是前面的二倍

每个$p_x$正好对应了点x到对应一侧子树根的路径长度呢!w就是中心边的长度

那么w是一样的,相当于点权附上$p_x+dep_x$,然后求个最大值,然后除个2

对于这个,我们拿出第二棵树建立虚树,在上面枚举LCA,先给边分治的两侧点赋格异色

如果LCA是u,那么我们有需要选子树中点权最大的两个异色点!

所以$dp_{u,1}$表示u子树内颜色1的点最大权是啥,$dp_{u,2}$表示u子树颜色2点最大权是啥

每次合并的时候动更新一次答案即可!

时间复杂度$O(nlog^2n)$被卡了

所以考虑建立虚树变成O(n)的

首先这个sort是可以基数排序qwq,就是说考虑

	inline void Sort(int* l, int *r){
		static int cnt[10], mx, key[N], tmp[N];
		mx=1;
		for(int *i=l; i<r; ++i) while(dfn[*i]>=mx) mx*=10;
		for(int o=1; o<mx; o*=10){
			for(int i=0; i<10; ++i) cnt[i]=0;
			for(int *i=l; i<r; ++i) key[*i]=dfn[*i]/o%10;
			for(int *i=l; i<r; ++i) ++cnt[key[*i]];
			for(int i=1; i<10; ++i) cnt[i]+=cnt[i-1];
			for(int *i=r-1; i>=l; --i) tmp[cnt[key[*i]]--]=*i;
			for(int *i=l; i<r; ++i) *i=tmp[i-l+1];
		}
	}

卧槽....

然后$Onlogn$预处理$O1$LCA

点分竟然也是可以的!

考虑进化一下那个dp,你会发现我们就算有一车颜色,也只需要记录两个异色最大权点即可......

然后合并两个子树就枚举4个可能异色的点对,然后再去选取这个最大的点进行合并即可qwq

真不错!

~~

P5610 [Ynoi2013] 大学

传统的套路是使用平衡树维护所有约数的倍数,然后直接平衡树合并即可,均摊是$O(nlog^2n)$的

这样被lxl点名卡掉了,只有题解可能卡的过去,我之前1s的范围卡进去了,现在卡不进去了

用内存池分配每个数的倍数,这里的空间一共是$w\ln w$的,然后考虑合并的时候,然后我们把所有的数的下标搞到他约数的对应的数组上,所以就可以二分直接找到所有区间内的数下标

写的时候要聪明一点就是每个数先拍到buc上,然后考虑从buc用$w \ln w$的复杂度跳一跳,就能知道每个数实际需要多少空间存下所有的数,就能静态内存了

然后除法的时候,先二分出那个下标区间,然后利用并查集找出每个数,如果这个数已经不能整除了就用并查集把这个数和下一个连通,相当于删除掉!

其他的用树状数组维护都不用说啦

P6781 [Ynoi2008] rupq

拨开题面正解可见

无视掉操作3,我们考虑前两个操作怎么维护

使用线段树,记录区间信息,显然一个区间内括号去掉匹配的会呈现")))((("这样的形态,我们只需要记录这个形态下的答案即可,不难看出翻转一个括号就是减少了一个匹配括号,而且只会消掉相邻近的

考虑区间合并,我们需要记录区间前缀左括号数,后缀右括号数

然后考虑中间匹配成功的那些怎么办,不难发现要么是左区间的右括号产生影响,要么是右区间的左括号产生影响

不妨设一个函数来log的求出这个信息!$solve(u,k,0/1)$表示节点u前k个右括号/后k个左括号的未匹配的括号max/0/1信息是什么

那么这个函数怎么递归呢?以左区间有剩余括号为例

查询前k个右括号$($

如果左区间的括号比右区间更多,而且足够,直接递归左边

如果不够,就是说我们的左区间括号太少了,假如我们节点记录了匹配后左/右区间剩余的信息,第一部分左区间的贡献在这里可以直接算,那么就是相当于还要用右区间一些信息,直接递归右区间剩余信息

如果右区间的括号比左区间多,直接递归右区间即可

后k个$)$括号

如果右区间的括号比左区间多而且足够直接右边

如果不够,说明我们右区间括号太少了............

有了这两个函数就可以直接解决前两问了,注意每个点还要维护合并后剩余的括号信息!

然后考虑操作3,我们要平衡树支持区间平移了,用fhqtreap维护即可

我特意飘了一眼$fhq$1e5的效率,最慢一个点57ms,还是很有希望干过去2e6的log的💢

复杂度$O(nlogn+mlog^2n)$

P5354 [Ynoi2017] 由乃的 OJ

对于30%的数据,$n,m<=1$

我会做这个!

考虑一个套路的东西,就是一个区间记录输入一个某个数某一位的值,然后能输出得到什么数

合并并不复杂,每个节点记录一个2元组,对应输入1/0输出??

于是你会发现一个路径也能够合并合并得到一个固定的答案,然后我们再考虑在这64位上每一位能填0得到1就填0得到1,否则能够填1就填1

这样直接做会TLE,所以你会发现每一位是独立的我们不需要重新建树,那么只需要记录一个[全0]输入得到什么数,[全1]输入得到什么数,然后再考虑合并

高明的地方来了!

我们考虑如何保留第二次操作的信息

即,如何在不显性知晓第二次操作的情况下知道第二次操作的信息

这个很关键也很简单:用1去&第二次操作

那怎么么去那些无用的信息?也很简单,用0去&

如果我们输入的都是0,得到左区间输出$h0$,于是我们有那些左区间输入为1的那些位的信息,可以直接&上右区间$f1$,于此同时删掉了0的个数所以再将这个取反,与右区间$h0$&即可,然后将信息再|起来即可

$h0'=(~hl0\&hr0)|(hl0\&hr1)$

$h1'=(~hl1\&hr0)|(hl1\&hr1)$

于是这道题就做完了....对2进制运算有了更深刻的理解?如果单纯看一位的还真不好看出来!

P6782 [Ynoi2008] rplexq

考虑根号分治,对于点的度数...

度数小于deg的

这告诉我们可以暴力枚举所有的儿子进行查询

然鹅,你会发现我们需要扫描线,即首先差分,变成$[1,r]-[1,l-1]$然后考虑在标号轴上左到右扫描,用分块支持$O(\sqrt n)$

修改和$O1$查询,这部分复杂度$O(n\sqrt n + q*deg)$

然后我们考虑怎么卡空间,这部分询问存储空间是$qdeg$的,显然不行

你发现我们其实只需要把x记到对应轴的左右端点上,然后查询时直接访问x的儿子都查询一次就好了

然后再考虑大度数点的部分.....

首先有一个做法,就是把所有的儿子染色,然后拿出来放到序列上排序离散一下,然后相当于一个经典问题:

$[l,r]$区间内所有颜色节点个数的平方和是什么?

不难用莫队做到$O(size\sqrt t_i)$

然鹅每个都这样做未免太蠢,你发现也可以暴力,这里暴力也是$qdeg$

所以可以二者取min,到时候再考虑选择哪个来转移

然鹅这样还是不够快,再加加速!

没有离散化掉的节点,也就是说$deg>\sqrt n$的节点,显然只有$\sqrt n$个

也就是说我们可以考虑对于他们开出一个数据结构,然后快速查询标号内区间和

线段树二分显然不行,还是分块

不将标号离散化,直接分块,因为如果离散化就变成了愚蠢的$\sqrt {nlogn}$,实现一个O1区间查询,这部分空间复杂度变成了$O(n\sqrt n)$

这里有一个牺牲代码复杂度争取时间的方法,每个子树维护一个线段树,然后线段树合并,直接区间查询前$\sqrt{\frac{ n}{logn}}$个重儿子

坏了,必然不行,线段树常数太大了

于是我们还有一个做法,考虑分块数组$\sqrt n$空间记录每一块的点数,然后直接块间前缀和,然后考虑块内前缀和如何维护

很快啊,你发现没法维护,这样一次询问就不是O(1)的,你命就没了

于是你发现,我们有个性质就是这$\sqrt n$询问区间端点相同,所以你可以对于所有边角块信息所有重儿子一起统计!也就是我们只维护块间前缀和,然后这样空间是对的

然后边角块我们可以直接枚举暴力!

具体的,我们用一个$O(n)$的数组记录每个标号为x的点是否出现,出现了在哪个子树中,然后对于一次询问,整块答案查询完之后把散块在这个数组上扫一遍,对应的子树个数加上即可

统计在哪个子树中可以在维护数据结构的时候顺带维护

时间复杂度就是$O(n\sqrt n + m\sqrt n+n\sqrt m)$的qwq

P6774 [NOI2020] 时代的眼泪

重糊时代的眼泪,我成为时代的眼泪

考场上2个人切了......你lxl不行!

第十三分块

分治套分块

先将整个平面用树套树分治,然后考虑观察如下事实

$ans_{abcd}=ans_{ab}+ans_{bd}+ans_{dc}+ans_{ac}-ans_{a}-ans_{b}-ans_{c}-ans_{d}+siza*sizd$

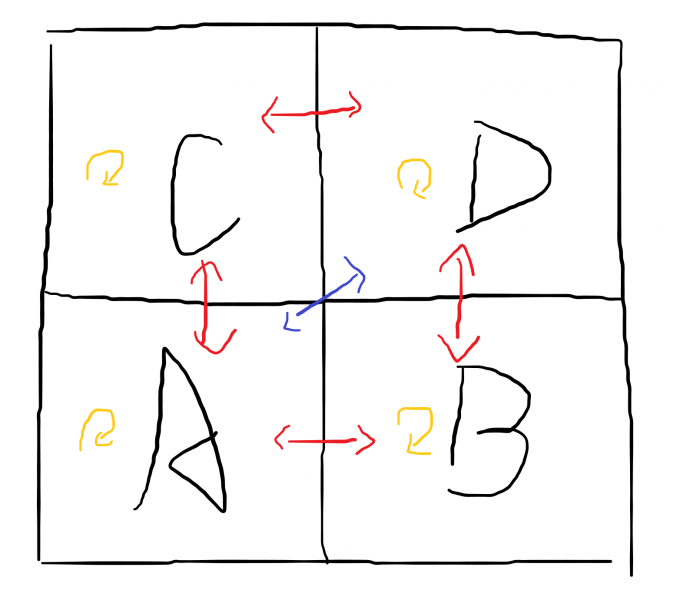
其中ad的贡献是平凡的,cb的贡献是0

把查询矩阵定位出来,我们有:

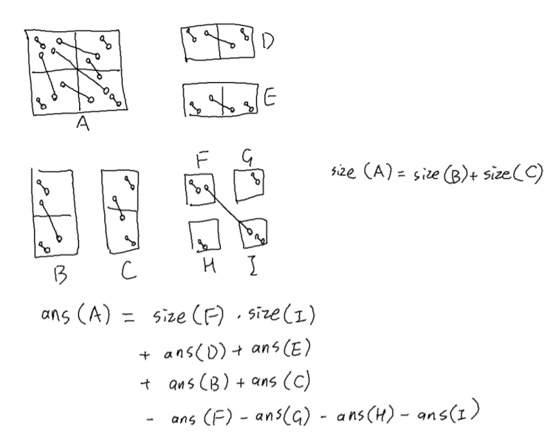
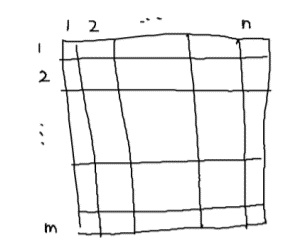
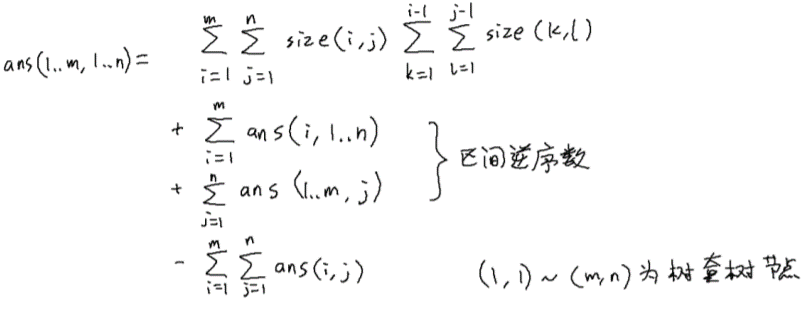
于是如果我们直接树套树上,可以做到两个log,然后递归到边界情况,变成一个区间逆序对

然后再仔细想想,你会发现这个区间逆序对还是一个值域逆序对,那他妈不是问题没有变简单吗??

我们给出的是一个排列,所以这个矩形内只会有w个点,这样的区间逆序对直接用暴力预处理,你会发现一次复杂度是$O\sqrt w$而每个长度的矩形只会出现1次,所以是可的,最后复杂度还是$O(n\sqrt n)$,但是常数巨大

分块做法:

区间逆序对怎么分块?

这是一个相当强力的问题,我们可以预处理$O(n\sqrt n)$的数组来解决,也可以二次离线

即,$cnt_{L,i,j}$表示i为左端点,第j块右端点为右端点这些块的区间逆序对数,同样的,处理一个i为右端点的,第j块左端点为左端点的

然后查询的时候先用这两个求和,再减去中间部分的,即处理$ans_{l,r}$表示l,r块的区间逆序对数

然后考虑如何预处理,处理前i块中小于等于j的数字个数,然后对于cnt数组,我们直接向后跳一整块进行求和

但是还有边角块的影响,这个预处理另一个数组表示i到i块左/右端点的$\leq a_i~~\geq a_i$数字不难解决

这两个数组就可以暴力了

然后如果l,r在同一块中,我们考虑容斥,对于位置i到$[i+1,R]$我们已经有答案了,但是没有i与$[r+1,R]$的答案

于是可以考虑预处理一个二维前缀和,这样子就能回答询问了qwq,就是暴力

本道题怎么做?

分3类case解决

1. 零零之间

   最好处理,排序后归并排序即可

2. 零零之内

   用二维前缀和,直接枚举每个数进行查询

3. 块零之间

   枚举一下零散块信息,然后直接暴力查询整块信息,这个可以用之前那个预处理的值域数组相减得到$[x,u]$之间的数数量

4. 块块之间

​ 如果能像零散块一样直接处理就好了,我们考虑还是一个前缀和,假如能枚举一个数u,然后查询$[L,k]$小于等于u的数数量就能做完了,而我们需要加速这个过程,所以还是不太$practical$

如果考虑容斥,我们要计算一个前缀的值域内顺序对数-两个值域相乘的顺序对数

后者相当好做,只需要预处理之前的数组即可,因为他的贡献是平凡的,$[L,k-1]$值$v<u-1$的数量*第k块中值$v \in [u,d]$数量

前者,一个$[1,c]$,$[l,r]$块的顺序对数,不是很简单啊

离线所有询问,扫描线,建立$\sqrt n * \sqrt n$平面,点(l,r)上记录第l到第r块的答案,你会发现我们每次加入一个数i,相当于对于某一块的一整行进行修改,这个修改是简单的,可以使用$O(1)$修改,而每次相当于查询一个矩阵的和,对于每行做前缀和即可,因为我们的列只有一个qwq

5. 整块之内

   这个直接预处理答案$\sqrt n*\sqrt n$的数组,是完全可以的

P6783 [Ynoi2008] rrusq

二维平面的根号算法:KDT

面积并显然要扫描线,维护左端点在l的答案

然后一个点尽可能的向后放即可

但是每次我们要更改的量级是$O(n)$的,再快也没用,$n^2$次修改....

变换下一个点的含义,考虑每个点代表其所代表矩形内所有点的信息

然后我们会发现,每次我们新增加一个矩形,在KDT上相当于$\sqrt n$个点的修改,这样$q\sqrt n$次修改分块即可

但是于此同时,我们要把一个点子树内所有代表点的信息全部删除,这个删除均摊$q\sqrt n$,根据kdt的复杂度分析,我们每次还是把整棵子树除了有标记的点外都遍历一遍就好!这样总复杂度还是$O(m\sqrt n)$的qwq

因为说我们删除一个点就会遍历到我们访问他遍历到的节点qwq

P6108 [Ynoi2009] rprsvq

硬看35min题解式子

$E=A * \sum_{i=1}^n{a_i^2}-B*\sum{ab}$

我们可以考虑算出所有平方项的系数和所有乘积项的系数

首先是平方项,枚举长度i后,考虑简单组合

首先有$\frac{1}{i}$的系数,然后对于任意一个长度为i的(a+b+c+d....)平方,会有i个平方项的贡献

又因为我们方差是$\sum({\frac{a^2+b^2+c^2...}{i}-(\frac{a+b+c...}{i})^2})$

也就是所谓的$\frac{1}{i}\sum a_i^2-x$,x是平均值,那么相当于枚举一个子序列,就有上式

而我们长度为i的子序列一共有$\binom{n}{i}$个,所以我们有单独一个平方项的贡献:$\frac{i-1}{i}\binom{n}{i}$

又因为我们元素本质相同,所以这个长度对于平方项总贡献就是$\frac{i-1}{i*n}\binom{n}{i}\sum(a^2)$

再考虑乘积项,也是一样的,有$\binom{n}{i}$选择产生乘积的子序列,每个会产生$i*(i-1)$个乘积项,然后对于他们有$\frac{1}{i^2}$的系数贡献,注意系数是-1化简后:

一共有本质不同的乘积项$\frac{n*(n-1)}{2}$,乘积项总贡献$-\frac{2*(i-1)}{in*(n-1)}\binom{n}{i}\sum(ab)$

n都是区间长度

然后我们再去考虑O(N)求出系数,就能直接$O(logN)$回答一组询问了!

$f_n=\sum_{i=1}^n\frac{i-1}{i}\binom{n}{i}$

拆开组合数

$f_n=-\sum_{i=1}^n\frac{1}{i}\binom{n-1}{i-1}+f_{n-1}+2^{n-1}$

那个东西是$\frac{\binom{n}{i}}{n}$

$f_n=\frac{2^n-1}{n}+f_{n-1}+2^{n-1}$

做完了

P6778 [Ynoi2009] rpdq

考虑分块,有个$c(n+m)\sqrt n $的不聪明做法qwq

首先考虑整块内的贡献,我们有1GB空间可以开$n\sqrt n$数组

但是这个题不需要在线,所以我们可以不用那么大的空间

考虑处理$f_{i,j}$表示i对于第j个块内所有点的答案

这个可以枚举一个块j,然后把j的点标记为关键点,然后直接$dp$,记录某个点到每个关键点的距离和,具体就是考虑子树中的关键点数有多少,然后处理出第一遍的所有点到根的答案,然后换根,考虑走一步会减少那些,增加那些,就能知道每个点到这个块内的答案

然后把这个数组前缀和,对于所有询问,处理掉这个块作为整块的与散块的/整块的块间贡献,同时也不难发现块内贡献也干掉了

然后这样我们再考虑处理散块即可

这里我们要先把每一块按照dfn序排序,然后归并排序实现dfn序的排序,这里$O(\sqrt n)$

然后再用$O1lca$实现虚树的建立,在虚树上dp一下即可,复杂度很低

这样我们就有$O((n+q)\sqrt n)$的做法了,好像过不去,要卡常

1. 把dfs函数变成dfn序上dp(艹)
2. 优化询问LCA的复杂度,减少栈部分的寻址复杂度
3. 改进第一部分判断?

比较恶心

P6109 [Ynoi2009] rprmq

考虑离线,把二维的信息扫描线下来

首先有暴力做法:把区间修改变为$l_1$时刻$[l_2,r_2]$加,$r_1$时刻$[l_2,r_2]$减

然后对于一个$[l_1,r_1]$时间区间的询问,我们暴力加入$1到l_1$之前的信息,然后再加入$[l_1,r_1]$的信息,并维护区间历史最大值即可,使用线段树,这个做法就是$O(nqlogn)$的

我们不妨考虑线段树分治来解决这个问题,即修改对应着一段时间区间,查询也对应了一段时间区间

但是我们需要把$[1,l]$的信息不记录的加入其中QAQ显然不能拆开一个区间进行回答

那么对于所有跨过$[l_1,r_1]$属于这个区间且跨过中间点mid的询问,我们挂在这个点上进行处理

假设现在我们已经有$[1,l]$(l是线段树区间左端点)的信息了

然后先处理右边对于答案的贡献,我们将$[l,mid]$的影响加入线段树(不记录最大值),然后从这里排序所有询问,从$[mid+1,r]$范围一次加入影响并进行回答即可

然后把$[mid+1,r]$信息清空,递归右子树(此时携带了$[1,mid]$的信息!)

再考虑一个节点左边的贡献,先把$l_1$从大到小排序类似的操作来递归左子树即可,类似于从后向前维护历史最大值,每次删掉前一个操作然后重新加回来qwq

不难发现每个线段树分治节点会被全部访问一次,复杂度就是$O(nlog^2n+qlogn)$

P6018 [Ynoi2010] Fusion tree

吐槽题目背景引入$O(n\sqrt{logn})$排序

大小分治是没跑了,如果没有操作1

我们发现大点大点的修改之间的影响可以直接算,小点修改对于大点的影响也可以直接算

小点查询也很简单,大点因为直接算了影响查询是O(1)的

于是有个操作1

我们不能按照度数分块了,考虑每个点建立一个trie树维护他的儿子信息,然后特殊判断父亲

操作1:相当于全局+1,父亲那边好维护,直接删掉然后重新插入进去即可

然鹅儿子这里就不太好了,需要trie的全局+1,要操作操作的

操作2:相当于改掉一个点的点权,只会影响他的父亲

操作3:查询trie树内所有信息的异或和,然后再异或上父亲的信息

你发现父亲的信息可能和父亲的父亲有关qwq所以再看看父亲的父亲的标记即可

P6019 [Ynoi2010] Brodal queue

第二个操作显然不弱于莫队,我们不能分治数据结构了

对于没有修改的情况,我们考虑树套树即可!

序列分块qwq

维护每个数的前缀出现次数以及前缀出现次数的平方,那么我们有:

$(a-b)^2=(a^2+b^2-2ab)$恒等式

所以我们还需要维护$2ab$,即所有颜色的前缀出现次数的乘积

设$f_{i,j}$表示前i个块,前j个块$\sum_x cnt(x,i)*cnt(x,j)$的值是什么

考虑如果我们将块k中某个颜色x点的出现次数$+g$

那么总有

$i\leq k,j \geq k$

变化量为$a*(b+x)-ab$,即加上$ax$

我们不难找到左端点为i的每个$f_{i,?}$来记录变化量

$i<k,j<k$

此时变化量为0

$i> k,j\geq k$

此时变化量为$(a+x)(b+x)-ab=ax+bx+x^2$注意a和i相关,b和j相关

所以把左端点为i的$f_{i,?}$打上标记维护变化量,右端点为i的$f_{?,i}$也打标记维护一下

然后$x^2$跟着即可

直接做是$O(\sqrt n)$修改的,我们可以差分做到$O(1)$,询问$O(\sqrt n)$

修改操作一看就很ODT,考虑推平性质,我们分块后,中间整块如果只有一个数直接$O1$

否则删掉一整块的信息,一个颜色的复杂度是$O(\sqrt n)$这里复杂度为$O(col * \sqrt n)$,删信息要做差分

均摊为$O((n+m)\sqrt n)$

最后查询我们可以用f,前缀平方和数组得到,但是对于只有一个颜色的块,我们没有使用f,所以要$O(\sqrt n)$扫一遍

有$(a-b+x)^2=a^2+b^2-2ab+x^2-2bx+2ax$,可以临时合并进去

P6105 [Ynoi2010] y-fast trie

分治这个值域我们有:

选择两个:

小于$C/2$和大于$C/2$直接贪心前两大

各选一个:

小于$C/2$个大于$C/2$首先贪心选二者最大值

然后就是可怕的对于一个值的区间最大值QAQ

插入一个元素我会做这个东西!只需要维护这个变化量每次动态查询就好啦!

删除一个啥么玩意????

如果可以离线,这个不难变成线段树分治

但是我们不行,考虑维护这个pair即数对,双向匹配最优化数对

一般我们都是要观察这个数对的性质,然后可行化的维护他!

假如i的最优匹配是j,j的最优匹配的k,$i<k$只需要考虑$(j,k)$这一个数对!这个结论很显然!

显然最多$O(n)$个,$multiset$维护一下即可O(nlogn)

你发现此时删除掉一个数,他至多只会有一个pair被影响,那么直接拿另一个数找到答案即可

注意每次我们要找最优匹配,最优匹配的最优匹配.....所以有点恶心

P5309 [Ynoi2011] 初始化

sb我的$O(n\sqrt n)$做法

显然对于大于$\sqrt n$的直接修改,利用分块块维护原来的前缀和

然后小于$\sqrt n$??

考虑对于x为周期的周期不会超过$\sqrt n$个

然后我们对于序列分段正好是$\sqrt n$一个长度的

那么可以对于一个x,维护一个前缀信息和和后缀信息和,然后直接算贡献

具体的,对于一整块[l,r],我们显然有答案

$\sum_{i=l}^ra_i+\sum_{i=1}^{\sqrt n}\sum_{j=1}^i(f_{i,j}*(\lceil \frac{r-j}{i} \rceil-\lceil \frac{l-1-j}{i} \rceil))$

md我是个撒子吗这个玩意$y<=x$!!!!

所以做完了直接预处理f数组的前缀和,就是先少算右端点的部分,然后加回来,然后多算左端点的贡献,再角去,即特判端点$(l-1)\%i$和$r\%i$即可qaq

P5311 [Ynoi2011] 成都七中

离线

建立点分树,每个询问挂在他点分树上对应点的代表连通块根上

那个点满足子树所有点在编号的集合是[l,r]的超集,而且x也在其中

同时有一个性质是树上任意一个连通块一定满足存在一个点分树上深度最小的点,整个连通块都在这个子树中qaq

一个点相当于$[mn,mx]$,表示u到根的经过编号最小最大的点,每次我们是数$[l,l],[r,r]$矩形中的颜色个数

然后对于每个点分树的子树,建立和节点上的询问扫描线模型,然后第一维从大到小扫,然后第二维直接用颜色做即可

具体的就是考虑排序所有点和矩形的第一维,然后第二维用一个线段树维护,每次把某个颜色的lst移动到这个mx即可

P5312 [Ynoi2011] 竞赛实验班

第四个操作很毒瘤啊,我们重点维护他!

然后看到第一个操作,你发现这个可以插入排序!具体的,我们可以考虑set优化插入排序之类的,一直维护前面一段有序,然后之后段都无序这样子,这样均摊是$O(nlogn)$的

然后看到第三个操作,我们异或可以巧妙的进行:打一个全局异或标记,每次插入新数的时候把那个数和这个标记异或起来

然后对于有序段的维护,你会发现因为我们已经知道他们是排序后的,所以可以直接用前k大代表下标$[1,k]$的前缀和

然后重新排序?因为是在异或意义下,你会发现这个$tag>>i\&1$就是相当于某一层我们交换一下左右儿子,并不需要真的交换,打标记即可qwq,相当于改变查询时走到哪个儿子

然后如果不排序我们操作3相当于没变,还是这样前k大找一下

插入没排序的时候就是前缀和数组向后延伸了一位而已

同时我们要插入一个数后排序?其实就相当于一个trie上的插入操作了,也不难实现qwq直接插入即可

注意这个和,是异或意义下的,因此我们要维护的是每一位有多少1的数组,故复杂度是$O(nlog^2A)$

P5313 [Ynoi2011] WBLT

不会啊/ll

莫队+区间bitset

首先对于每个询问可以莫队得到这个区间的bitset

然后把这个bitset分个块,如果这个b足够大的话,我们可以直接从左到右每b个and起来

这部分复杂度是$O(m*\frac{n}{b}*\frac{b}{64})$

但是较小的时候就不行了,直接TLE了,虽然看上去和b没什么关系,但是我们提出$n/b$块就T了啊

你会发现这样的b不会很多,那么我们可以考虑莫队询问的每一个b,即对于一个b开b个bitset,表示$mod~b$同余i的所有数出现情况,然后莫队维护即可

然后直接判断一个区间的答案就是对于每个bitset取mex然后最大值

这部分复杂度也是$O(n\sqrt n)$,但是空间交劣一些,不过也是$O(\frac{nb}{64})$

P5607 [Ynoi2013] 无力回天 NOI2017

先看

SP16549 QTREE6 - Query on a tree VI

有个naive的做法是LCT维护连通块,这样会TLE在菊花图

其实也不需要,只要来几次对于度数很大的点询问即可

说不定我们是可以用根号分治来维护的,我太菜了不太会啊

把每个点的父边赋予这个点的颜色,然后每次在对应的颜色的LCT上修改这个边的信息就做完了

因为此时连通块变成了去掉父亲节点的连通块信息啊!然后你会发现如果我们还是用原图的点作为点的话,相当于给了个机会让我们整合信息!让度数大的便于维护了

而此时我们有去掉一个点后对应子树的大小一回事,这个直接找到根到这个子树第一个点的子树大小即可,用findroot后右子树第一个点即可qwq

---

回看本题

考虑一个很毒瘤的转换:n种颜色比较困难,但是两种颜色很简单

而且是问存在一个黑点的路径数

我们可以考虑容斥,答案相当于总路径数减去每个白色连通块大小的平方,可以预处理

当改变颜色的时候,我们相当于这个点要变动的...那么就是把它贡献加上这些连通块大小两两相乘的和,相当于$(x+y)^2=(x^2+2xy+y^2)$,$(x+y+z)^2=(x^2+y^2+z^2+2xy+2xz+2yz)$

但与此同时多了一个点,所以要加上$x+y+z+...+1$

然后LCT维护点的信息即可,用维护边代替....

但是说这才两种颜色啊

你发现n中颜色,等价于我们将时间轴拆开为相同颜色的几次修改,然后在每一段时间轴相邻部分做两种颜色的贡献,当然是在一开始预处理好了之后

那么我们对于所有颜色排序后依次处理,然后对于时间轴做一个差分加法求前缀和就好了!

P5527 [Ynoi2012] NOIP2016 人生巅峰

原题啊喂csp网站上都有的

长度大于等于14直接GG了

然后区间立方可以用线段树维护多少次的吧喂

然后可以预处理1000以内的信息?

然后这个14的有没有和判断的过程可以折半搜索的....

P5528 [Ynoi2012] WC, THUWC, CTSC 与 APIO2017

看上去很时间分治,实际上你推平就TLE/cy

对于度数大于$\sqrt n$的直接考虑一个叫做$BFS$序的东西

你发现一个距离为k的所有点和在x的BFS序上是几段连续的区间!

因此我们直接预处理所有点的BFS序,然后暴力跳来维护修改即可

度数小于$\sqrt n$的点

你会发现这个可以数据结构维护一下,开一个辅助树森林,这个树上点x就对应一个点在原树上的k级祖先,然后对于一个修改如果y=0相当于辅助树上连续棵子树的修改

如果y!=0,不难发现应该找到第一个和y同余的那些点,这些点在原树bfs序上显然是连续的区间,这样的点数可能会很多,但是他们对应的在辅助树上的dfs的k级祖先也是连续的,所以我们可以直接提出这段区间,然后对于这一段区间直接修改,具体就是一个区间取min取max的操作,不需赘述了

不难发现我们第一个操作要$O1$修改$O(\sqrt n)$的查询,第二个操作要$O\sqrt n$修改$O1$查询,反正它都是可以分块的

注意空间是$O(n\sqrt n)$的/jk

其实还有一条道路是时间轴分块,但是对于$x<\sqrt n$的操作很难推平QAQ,所以可以玄学运用结合法?

P5529 [Ynoi2012] 梦断 SCOI2017

你妈的梦断是没进A队

没有操作3那几个诡异的询问怎么做?

如果gpa至多两种,那么你会发现操作1相当于连通块分裂然后合并,操作2也相当于提出一个连通块进行合并

而你会发现分裂简单,每次都只能分裂出一个,但是合并连通块可能合并很多,这里根据均摊复杂度正确是可以暴力修改,因为每次一定会导致合并

30个就gg了/cy

没有题解

lxl说ETT就能做,不需要高级动态树,显然是高估了我:

P5607 [Ynoi2013] 无力回天 NOI2017

区间线性基区间异或修改

首先前者可以线段树维护线性基的每一个位置数是什么,合并直接区间线性基合并即可,这个复杂度就是$O(nlognlog^2A)$的/jk

然后区间修改,考虑我们时间复杂度反正已经上天了,那就再炸裂也没什么了直接将区间信息提出来然后都xor一遍然后重新建立线性基即可,反正复杂度还是三个log......

不过这样萎了,因为显然这个东西是xor会改变线性基的线性相关性,所以我们考虑变成一个前缀信息,即差分数组

其中$a_l=XOR_{i=1}^lb_l$

那么你会发现对于$a_l...a_r$构成的区间线性基,我们总会和$a_l+b_l...b_r$构成线性基相同

因为线性基又没有限制你选多少个数,所以重复选择一定能$xor$出a中所有的数,然后再就完了

那么现在就是怎么维护b的线性基,这个可以变成单点修改完成,这样就能三个log维护啦~

然后还要一个数据结构维护a别忘了

正式开始Ynoi大分块系列

P5397 [Ynoi2018] 天降之物

弑尽破净的第四分块

序列分块做法:

考虑处理每一块的颜色两两处理一个$\sqrt n*\sqrt n$的一个数组,并且记录每个颜色最左和最右的位置,然后你会发现查询的操作很好维护,直接四个都算一下,然后相邻两块之间/零散块内算一下就好了

但是修改不简单,我们每个块要很快才行,你会发现可以巧妙均摊

1. x,y相同
2. x不存在
3. y不存在
4. x,y都存在

此时你会发现我们可以O(1)修改其他某种颜色对于这个颜色的答案,相当于二者取min

然后这两种颜色合并他们的信息得到其他的信息要O(m)扫一下其他所有颜色

你发现我们每次使用$\sqrt n$的时间让$\sqrt n$的颜色减少了1,所以均摊是$m\sqrt n$是对的qaq

根号分治

大的维护一个数组:和其他的答案

小的暴力

考虑合并怎么办

小小合并

有什么用?把对应位置的数组归并到一起即可,如果大于$\sqrt n$,暴力构建整个数组即可

大大合并

暴力每个位置取min即可,因为我们不会合并超过$\sqrt n$次

小大合并

你发现此时我们可以预处理这样一个数组$pre_{i,j}$表示大颜色i并入小颜色j后的答案

因为min具有可以合并性质,所以我们直接记录这个大颜色挂了多少小颜色

但是这个预处理数组好像并不简单啊QAQ我们直接MLE了

再善用一下,我们并入这个集合的颜色个数每$\sqrt n$达到$\sqrt n$就重构

否则拿出来那些颜色,和询问做归并即可

做完啦!

P4117 [Ynoi2018] 五彩斑斓的世界

突刺贯穿的第二分块

都说是基础.....我基础也不会/ll

没有修改可以记录每块中排名为i的出现的值是什么

然后把这个数组前缀和话,就是前i块中出现次数为j的值是什么,这个数组的大小是$O(n\sqrt n)$的,可以支持$O(log)$回答

啥啊....这个主席树就好了.....

这个修改操作我实在难以维护啊QAQ

分块,每块的最大值为k,你会发现我们每次修改的数为x的话:

$2x>k$直接全部减,我们把$[x+1,v]$的数的值合并到$[1,v-x]$上

$2x<k$,打一个全局减x标记,把小于x的加上x,然后把$[1,x]$的值合并到$[x+1,2x]$上去

不难发现我们每次都使用$O(x)+O(维护)$得最大值减少$O(x)$的量

如果这个维护$O1$,那么总复杂度就是$O(vb)$的了

也就是说我们要$O1$把x的值合并到x+v上去,$O(\sqrt n)$查询具体一个数的值

不难发现这个东西可以使用链表维护,但是对于内存不友好的链表会很慢QAQ,重构的时候遍历即可

那么我们可以通过vector的启发式合并加速这个过程qwq,不过虽然是log的但是可能会快一点

并查集,本质上和链表差不多,但是常数好很多qaq

离线逐块处理做到$O(m+n)$空间

P6578 [Ynoi2019] 魔法少女网站

第十分块

这个漫画是什么乐色东西??别看啊别看啊

不带修?莫队不太行,分块吧

$f_{i,j}$表示第i块最大值小于等于rank为j的子区间个数,这个数组大小是$O(n)$

处理$pre_{i,j},suf_{i,j}$表示第i块排名为j的最左边/右边的位置是啥,方便合并相邻两块的信息

特判一整块都没有的情况,如果我们一块一块的考虑贡献,甚至不需要离散化

可不可以考虑把所有询问按照x排序后依次处理啊?

这个也是可以的.....对于带修改不强制在线的询问离线唯一方法:时间分块

每$\sqrt n$个放在一起做,然后只需要随便推平即可

现在相当于维护一个01序列,然后每次我们会将其中几个0变为1,1变为0,问区间0段的长度平方和

序列分块

显然1变为0好做,直接左右两端合并信息即可

0变为1不好做,此时要分裂区间

但是0变为1不可能是因为值域加入导致的,是修改操作导致的,所以这些位置可以空出来,然后回答一个询问可以原地撤销掉他们(变成1),然后再反着挨个变为0就能维护一块的信息了

然后查询的时候做到$O(\sqrt n)$即可

最后注意时间分块的块大小大一点,序列分块的稍稍小一点$O(\sqrt {0.8n})$