“我认为遭人辱骂为【伪善者】之人，才有成为【英雄】的资格。放眼古今英雄做下的决断，时而残酷，时而无情，时而不被人所原谅，但其意志却无比珍贵而又无可取代，以愚者自居吧，贝尔”——费尔斯.

~~要找张贝尔图怎么这么难,你知道搜地下城全是赫斯提亚的绝望吗~~

访问此篇可能找不到您想要的数学知识

因为是省选起步上不封顶的

二次剩余

对于 $x^2 \equiv n (mod p)$ ,能满足n是%p二次剩余的n一共有 $(p-1)/2$ 个,非二次剩余有 $p-1/2$ 个

证明:

不妨证明 $x \in [1,p-1/2]$ 他们的 $x^2$ 两两不同

因为说如果这些成立,那么又有 $(p-x)^2 \equiv x^2 (mod p)$ ,所以说我们的解在 $x \in [1,p-1/2]$ 即可取到,而如果这 $p-1/2$ 个解两两不同,那么我们至少有满足条件的解数量,同时其余的x取值和之前的某一个一定重复,所以这也是恰好的总共的可能的解的数量

假设存在x,y他们满足 $x^2\equiv y^2 (mod p),x!=y$

根据平方差有 $(x-y)(x+y)\equiv 0 (mod p)$

又因为x,y都是 $[1,p-1/2]$ 的数,那么 $x-y,x+y$ 都不可能为0/-p/p啊

所以不存在平方相同的不同数x,y

证毕

勒让德符号

~~狼人的符号~~

对于 $mod p$ 意义下定义的

if p不整除n 是二次剩余

-1

if p不整除n 不是二次剩余

if p整除n

记做 $\left(\frac{n}{p}\right)$

看上去是这样的

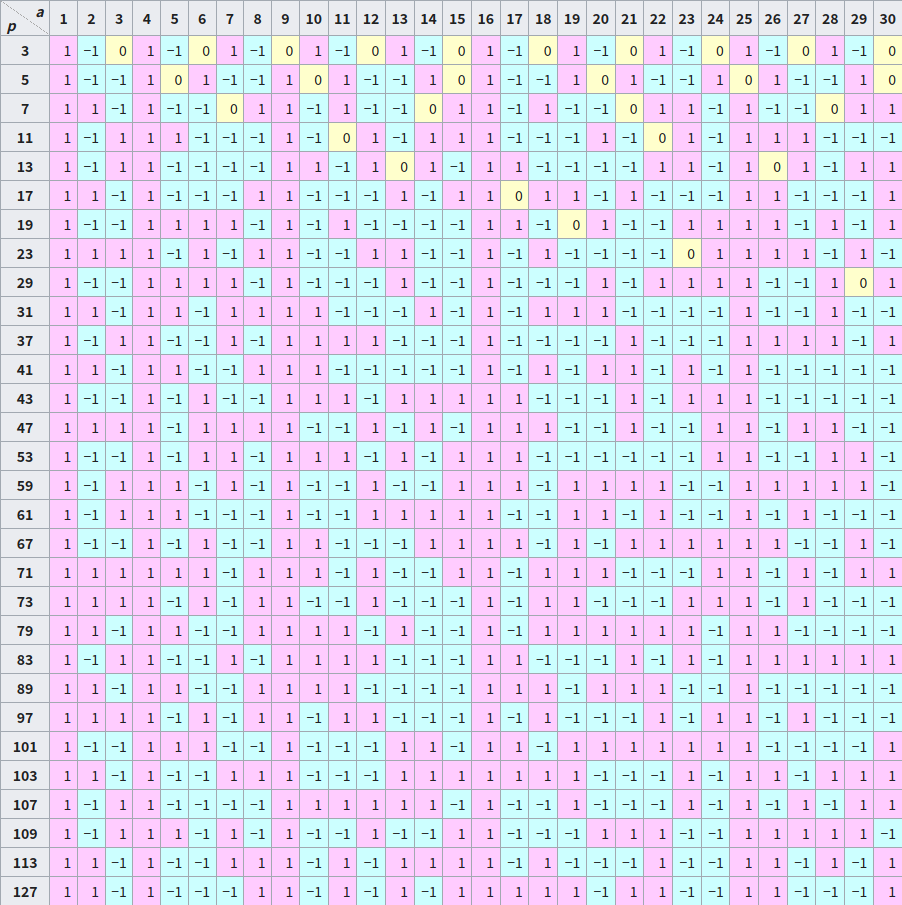
欧拉判别准则

\left(\frac{n}{p}\right) \equiv n^{\frac{p-1}{2}} (\mod p)

若n是二次剩余,当且仅当 $n^{\frac{p-1}{2}}\equiv 1$

n不是,当且仅当 $n^{\frac{p-1}{2}}\equiv -1$

证明还是平方差!

费马小定理

n^{p-1}\equiv 1 (mod p)

(n^{\frac{p-1}{2}}+1)*(n^{\frac{p-1}{2}}-1)\equiv 0

左边两项一定有一个是p的倍数,所以说在mod p意义下 $n^{\frac{p-1}{2}}$ 要么是1要么是-1

假设为1

p是一个奇素数,就有关于p的原根存在

g为p的一个原根,于是我们就有 $g^k\equiv n$

g^{k*\frac{p-1}{2}} \equiv 1

根据原根的定义可知 $g^{p-1} \equiv 1$

所以 $p-1$ 整除 $k*\frac{p-1}{2}$

于是k必然是一个偶数

那么我们发现对于 $i=j/2$

${a^{2*i}}=n$

那么 $a^i$ 就是一个平方等于n的数

这相应的也给出了一个解:

$x^2=n$

一个n为二次剩余,那么求出原根对于他的表示,这个表示/2的原根次方就是对于一个可行的x

$\sqrt n$ ~~乐色算法~~

Cipolla 算法

~~大标题~~

$O(log)$ 神仙算法

找到一个数a,满足 $a^2-n$ 是非二次剩余,其实我也不知道为什么想到找非二次剩余......

建立一个复数域,定义其中的 $i=a^2-n$

那么我们一定可以把所有数表示为 $A+Bi$ ,AB都是模意义下的数

如果找到了这个a,我们可以直接找到答案, $x^2 \equiv n (mod p)$ 解为 $(a+i)^{\frac{p+1}{2}}$

怎么找a?你觉得非二次剩余多不多啊?所以说我们直接在P范围内随机这个a,期望两次找到答案

证明:

~~结论1我记得qbxt考过~~

(a+b)^p \equiv a^p+b^p (mod p)

证明方法:二项式展开,其中所有中间的项都会带上一个组合数,那个组合数里面一定有一个因子是p,因此在mod p意义下都是0,只有两边的项没有那个p因子qwq

结论2

i^p\equiv -1 (mod p)

i^p \equiv i^{p-1}*i

\equiv i^{2*{p-1}/2}*i

\equiv (a^2-n)^{{p-1}/2}*i

~~勒让德冲~~

\equiv -1*i

注意到这个地方我们定义的非二次剩余起效了!

开始推导

x \equiv (a+i)^{p+1/2}

\equiv ((a+i)^{p+1})^{1/2}

\equiv ((a+i)^{p}*(a+i))^{1/2}

\equiv ((a^p+i^p)*(a+i))^{1/2}

$a^p \equiv a$ ,费马小定理....

\equiv ((a-i)*(a+i))^{1/2}

\equiv (a^2-i^2)^{1/2}

\equiv (a^2-(a^2-n))^{1/2}

\equiv (n)^{1/2}

x \equiv (a+i)^{p+1/2} \equiv (n)^{1/2} (mod p)

因此确实找到了一组解,也就是从此之后,我们可以 $O(log)$ 模意义下开根号了

P5491 【模板】二次剩余

写的时候确实要注意重载运算符写复数类qwq

需要的只有实数部

有的数是开不了根的,也就是非二次剩余


//(a+i)^{p+1/2}
//i=a^2-n
#include<bits/stdc++.h>
using std::swap;
#define ll long long
ll T, n, P;
ll i2;
struct Cmpl {
	ll A, B;
	Cmpl(ll x = 0, ll y = 0): A(x), B(y) {};
} qwq;

Cmpl operator*(Cmpl x, Cmpl y) {
	Cmpl c = Cmpl(0, 0);
	c.A = (x.A * y.A % P + x.B * y.B % P * i2 % P) % P;
	c.B = (x.A * y.B % P + x.B * y.A % P) % P;
	return c;
}

inline ll mrand() {
	return 1ll * rand() * rand() + 1ll * rand() * (rand()^rand());
}

//复数意义的乘法
inline Cmpl ksmC(Cmpl x, ll y, ll P) {
	Cmpl ans = Cmpl(1, 0);
	while(y) {
		if(y & 1)ans = ans * x;
		x = x * x;
		y >>= 1;
	}
	return ans;
}

inline int chk(ll x, ll P) {
	return ksmC(Cmpl(x, 0), (P - 1) / 2, P).A == P - 1;
}

//模意义开根
inline ll getsqrt(ll n, ll P) {
	n %= P;
	ll ans = 0;
	while(1) {
		ans = (mrand() % P + P) % P;
		i2 = (ans * ans % P - n + P) % P;
		if(chk(i2, P)) {
			return ksmC(Cmpl(ans, 1), (P + 1) / 2, P).A;
		}
	}
	return -1;
}


int main() {
	srand(time(0));
	scanf("%lld", &T);
	while(T-- > 0) {
		scanf("%lld%lld", &n, &P);
		if(n == 0) {
			puts("0");
			continue;
		}
		ll p1 = getsqrt(n, P);
		if(p1 == -1 || p1 == 0) {
			puts("Hola!");
			continue;
		}
		ll p2 = P - p1;
		if(p1 > p2)swap(p1, p2);
		if(p1 == p2) {
			printf("%lld\n", p1);
		} else printf("%lld %lld\n", p1, p2);
	}
	return 0;
}
//11 1e9+9

类欧几里得算法

洪华敦爷爷提出的/se

绝妙!

设

f_{a,b,c,n}=\sum_{i=0}^n\lfloor \frac{ai+b}{c} \rfloor

$log n$

数论分块是不可能的,我们可以发现能够对于a,b预处理,当他们大于c的时候

f_{a,b,c,n}=\sum_{i=0}^n\lfloor \frac{(\lfloor\frac{a}{c}\rfloor + a mod c)i+\lfloor\frac{b}{c}\rfloor + b mod c }{c} \rfloor

于是我们有

f_{a,b,c,n}=\sum_{i=0}^n\lfloor \frac{a mod c~~i+b mod c }{c} \rfloor + n*(n+1)/2\lfloor \frac{a}{c} \rfloor+\lfloor \frac{b}{c} \rfloor*n

我们能够递归到两个都小于的情况,下面解决这种情况

要加快一个和式的计算过程，所有的方法都可以归约为贡献合并计算。-OIwiki

所有求和式的优化都在于合并计算贡献这一项,也就是说我们可以把条件和贡献做转换得到另一个式子

条件 $i<n$ ,贡献为 $\sum_{i=0}^n\lfloor \frac{ai+b}{c} \rfloor$

\sum_{i=0}^n\lfloor \frac{ai+b}{c} \rfloor = \sum_{i=0}^{\lfloor \frac{ai+b}{c} \rfloor - 1}\sum_{j=0}^n[i<\lfloor \frac{aj+b}{c} \rfloor]

相当于枚举多少个数符合,然后里面那个东西很不友好,我们直接处理他(i,j互换了)

j<\lfloor \frac{ai+b}{c} \rfloor

根据具体数学中去掉底符号,我们可以变成加一后小于等于就去掉了,因为小于等于是否整除都没关系了

j+1<=\lfloor \frac{ai+b}{c} \rfloor

j+1<=\frac{ai+b}{c}

jc+c<=ai+b

但是加上下取整符号,我们又需要这个小于??

\lfloor\frac{jc+c-b-1}{a}\rfloor<i

于是我们这个条件把i解放了,也就能够把i消掉了

m=\lfloor \frac{an+b}{c} \rfloor

f_{a,b,c,n}=\sum_{j=0}^{m-1}\sum_{i=0}^n[i>\lfloor \frac{jc+c-b-1}{a}\rfloor]

t=\lfloor\frac{jc+c-b-1}{a}\rfloor

f_{a,b,c,n}=\sum_{j=0}^{m-1}\sum_{i=0}^n[i>t]

=\sum_{j=0}^{m-1}n-t

=nm-f_{c,c-b-1,a,m-1}

于是我们发现就能够向问题规模更小的方向去递归了,同时我们分母间互换了位置

惊人的,我们直接实现就是log的,因为类似于辗转相减

接下来我们再推导两个函数才能得出模板题的解:

h_{a,b,c,n}=\sum_{i=0}^n\lfloor \frac{ai+b}{c} \rfloor^2

g_{a,b,c,n}=\sum_{i=0}^n\lfloor \frac{ai+b}{c} \rfloor *i

感觉上并不复杂,其实推推.....

先h

取模

h_{a,b,c,n}=\sum_{i=0}^n\lfloor \frac{(\lfloor\frac{a}{c}\rfloor + a mod c)i+\lfloor\frac{b}{c}\rfloor + b mod c }{c} \rfloor^2

展开,把其中两项放在一起,得到一个9项式,合并同类项后可得

h_{a,b,c,n}=\sum_{i=0}^n\lfloor \frac{a mod c~~i + b mod c }{c} \rfloor^2 + \frac{a}{c}^2\frac{n*(n+1)*(2n+1)}{6}+\frac{b}{c}^2*(n+1)+2*(\frac{a}{c}+\frac{b}{c})+\frac{a}{c}\frac{b}{c}*n*(n+1)

/yun?qwq

解决求和问题

按照传统套路,我们应该枚举答案的类似思路,但是首先我们要做一歩必要的转换

n^2=n*(n+1)/2-n

也就是说我们可以枚举里面那个东西了

h_{a,b,c,n}=\sum_{i=0}^n [2*\sum_{j=1}^{\lfloor \frac{ai+b}{c} \rfloor}j-\lfloor \frac{ai+b}{c} \rfloor]

=\sum_{i=0}^n 2*\sum_{j=1}^{\lfloor \frac{ai+b}{c} \rfloor} j - f_{a,b,c,n}

=\sum_{i=0}^n 2*\sum_{j=0}^{\lfloor \frac{ai+b}{c} \rfloor-1} (j+1) - f_{a,b,c,n}

2 * \sum_{i=0}^n \sum_{j=0}^{\lfloor \frac{ai+b}{c} \rfloor-1-1} (j+1)

=2 * \sum_{j=0}^{m-1} (j+1) \sum_{i=0}^n [\lfloor \frac{ai+b}{c} \rfloor > j]

=2 * \sum_{j=0}^{m-1} (j+1) \sum_{i=0}^n [i > t]

=2 * \left( \sum_{j=0}^{m-1} j \sum_{i=0}^n [i > t] + \sum_{j=0}^{m-1}\sum_{i=0}^n[i>t] \right)

=2 * \sum_{j=0}^{m-1} j*(n-t) + 2*\sum_{j=0}^{m-1}(n-t)

下面g',f'表示下一层递归下去的函数值

=m*(n-1)*n + 2*nm-2*g'-2*f'

=m*(n+1)*n-2*g'-2*f'

qwq整完了,最后

h_{a,b,c,n}=m*(n+1)*n-2*g'-2*f'-f

本质上可能是容斥呢,g函数一样的推法,就不写了

写代码的时候小心那个递归进入的是m-1

以及乘法m要取模.....

code:


#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int P = 998244353;
const ll inv2 = (P + 1) / 2;
const ll inv6 = 166374059;

int T, a, b, c, n;
struct rec {
	ll f, g, h;
};

inline rec solve(ll a, ll b, ll c, ll n) {
	rec ret = {0, 0, 0};
	ll ac = a / c;
	ll bc = b / c;
	if(a == 0) {
		ret.f = bc * (n + 1) % P;
		ret.h = bc * bc % P * (n + 1) % P;
		ret.g = bc * n % P * (n + 1) % P * inv2 % P;
		// printf("a==0 : %lld %lld %lld\n", ret.f, ret.g, ret.h);
		return ret;
	}
	// printf("%lld %lld %lld %lld %lld\n", a, b, c, n, m);
	if(a >= c || b >= c) {
		rec gt1 = solve(a % c, b % c, c, n);
		ret.f = (gt1.f + n * (n + 1) % P * inv2 % P * ac % P + (n + 1) * bc % P) % P;
		ret.g = (ac * (n + 1) % P * ((2 * n + 1)) % P * n % P * inv6 % P +
				 bc * n % P * (n + 1) % P * inv2 % P +
				 gt1.g) % P;
		ret.h = (ac * ac % P * (n + 1) % P * ((2 * n + 1)) % P * n % P * inv6 % P +
				 bc * bc % P * (n + 1) % P +
				 2 * bc % P * gt1.f % P +
				 2 * ac % P * gt1.g % P +
				 bc * ac % P * n % P * (n + 1) % P +
				 gt1.h) % P;
		return ret;
	}
	ll m = (a * n + b) / c;
	rec gt = solve(c, c - b - 1, a, m - 1);
	m %= P;
	ret.f = n * m % P - gt.f;
	ret.f = (ret.f % P + P) % P;
	ret.g = ((n * m % P * (n + 1) % P - gt.h - gt.f) % P + P) % P * inv2 % P;
	ret.g = (ret.g % P + P) % P;
	ret.h = n * (m + 1) % P * m % P - 2 * gt.g % P - 2 * gt.f % P - ret.f;
	ret.h = (ret.h % P + P) % P;
	// printf("%lld %lld %lld %lld\n", gt.f, ret.f, ret.g, ret.h);
	return ret;
}

int main() {
	scanf("%d", &T);
	while(T-- > 0) {
		scanf("%d%d%d%d", &n, &a, &b, &c);
		rec qwq = solve(a, b, c, n);
		printf("%lld %lld %lld\n", qwq.f, qwq.h, qwq.g);
	}
	return 0;
}

P5171 Earthquake

我觉得这个题放在例题很不错很不错qwq

然后有个trick就是分子小于0你是不能递归的,因此此时会出现交换分子分母后都没有缩小问题规模的情况

所以说我们直接让分子加上分母即可,然后在最外面角去

\sum_{i=0}^{n}(\frac{-ax+c}{b}+1)=\sum_{i=0}^{n}\frac{(b-a)x+c}{b}+n+1-n*(n+1)/2

P5172 Sum

喜闻乐见的类类欧题,我们先来做一下转换

(-1)^x=1-2*(x mod 2)

=1-2x+4*\lfloor\frac{x}{2}\rfloor

只能说很妙我不知所措,就是把-1指数上的东西放下来的一种方式

Ans=n-\sum_{i=1}^n\lfloor d \sqrt{r}\rfloor*2+\sum_{i=1}^n\lfloor \frac{d\sqrt{r}}{2} \rfloor

于是我们想求里面这个东西,然后有个妙绝的式子

f(a,b,c,n)=\sum_{i=1}^n\lfloor \frac{a\sqrt{r}+b}{c} i\rfloor

求这个东西答案也就显然了

我们考虑设

x=\sqrt{r}

t=\frac{ax +b}{c}

于是啊,我们有

$t>1$
$t<1$

两种情况,可以放毒

$t>1$

f(a,b,c,n)=\sum_{i=1}^n\lfloor ti + \lfloor t \rfloor i -\lfloor t \rfloor i\rfloor

f(a,b,c,n)=\sum_{i=1}^n\lfloor \frac{ax+b-c*\lfloor t \rfloor}{c}\rfloor \lfloor t \rfloor *n(n+1)/2

b变小了,也就是说我们的t变小了

不难发现如果t小于1,t下取整是0,没什么意思qwq

$t<1$

分母有理化

f(a,b,c,n)=\sum_{i=1}^n\lfloor \frac{ax+b}{c} i\rfloor

m=\lfloor \frac{ax+b}{c} n\rfloor

f(a,b,c,n)=\sum_{i=0}^{m-1}\sum_{j=1}^n\left[i< \frac{ax+b}{c} j\right]

\left[ci< {ax+b}* j\right]

\left[\frac{ci}{ax+b}< j\right]

f(a,b,c,n)=n*m -\sum_{i=0}^{m-1}\lfloor \frac{c}{ax+b}\rfloor

f(a,b,c,n)=n*m -\sum_{i=0}^{m-1}\lfloor \frac{acx-bc}{a^2x^2-b^2} i\rfloor

注意到我们可以向下递归了!因为分母以及分子中除了x都是有理数!

那么我们这样递归下去

然后你想边界是啥啊?你发现因为 $t<1$ 所以我们的m(n)一定在减小....所以直接当m减小到1级别的时候判掉即可!

code:

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define db double
#define exll ll

int T,n,r;
db rr;

inline ll gcd(ll x,ll y) {
	return y==0?x:gcd(y,x%y);
}

inline exll solve(ll a,ll b,ll c,ll n) {
	if(n==0)return 0;
	ll t=(a*rr+b)/c;
	if(n==1)return t;
	if(t!=0) {
		exll ret=(exll)t*n*(n+1)/2;
		ret+=solve(a,b-c*t,c,n);
		return ret;
	} else {
		ll na=a*c;
		ll nb=-b*c;
		ll nc=a*a*r-b*b;
		ll g=gcd(na,nc);
		g=gcd(nb,g);
		na/=g;
		nb/=g;
		nc/=g;
		exll ret=((a*rr+b)/(db)c*n);
		ret=ret*n-solve(na,nb,nc,(ll)((a*rr+b)/(db)c*n));
		return ret;
	}
}

int main() {
	scanf("%d",&T);
	while(T-->0) {
		scanf("%d%d",&n,&r);
		rr=sqrt(r);
		if(ceil(rr)==floor(rr)) {
			if((int)rr&1) {
				printf("%d\n",-1*(n&1));
			} else printf("%d\n",n);
			continue;
		}
		ll ans=n-2*solve(1,0,1,n);
		ans += 4*solve(1,0,2,n);
		printf("%lld\n",ans);
	}
	return 0;
}

P5221 Product

~~(完了完了整理不完了)~~

看上去一个样,但是想想完蛋了

时间限制 200ms
内存限制 7.81MB

这意味着什么呢?1e6的数组不能开多了

\prod_{i=1}^n\prod_{i=1}^n\frac{ lcm(i,j)}{ gcd(i,j)}(mod 104857601)

\prod_{i=1}^n\prod_{i=1}^n i*j *\prod_{i=1}^n\prod_{i=1}^n \frac{1}{\gcd(i,j)^2}

\prod_{i=1}^n\prod_{i=1}^n i*j

你仔细冷静一下,这个有n^2项,而且每一项是一个乘积的形式,所以一定有至少 $2*n^2$ 项吧

然后亡命重排列一下,你会发现固定i,j是一个n!阶乘,固定j,i是一个n!

一共有 $2n$ 个 $n!$

所以这部分答案是 $(n!)^{2n}$

后面部分毒瘤啊,我们发现是负二次方可以提到外面,然后枚举gcd

\prod_{d=1}^n d \prod_{i=1}^{n/d}\prod_{i=1}^{n/d} [gcd(i,j)==1]

你会发现啊,这个如果后面都是连乘,而且都是1的话,就是

\prod_{d=1}^n d^{\sum_{i=1}^{n/d}\sum_{i=1}^{n/d} [gcd(i,j)==1]}

而且,我们能有一个可爱的结果,因为循环枚举的上界是一样的,这个东西就和欧拉函数的定义一样

\prod_{d=1}^n d^{2*sum_phi[n/d]-1}

最后是

(n!)^{2n} *(\prod_{d=1}^n {d^{2*sum_{phi[n/d]}-1}})^{-2}


#include<bits/stdc++.h>
#define ll long long
const int MAXN=1e6+1;
const int P=104857601;
using namespace std;

int N,tot;
int phi[MAXN],pri[MAXN];
bool isp[MAXN];
ll ans;

inline ll ksm(int x,int y) {
	ll ans=1;
	while(y) {
		if(y&1)ans=ans*x%P;
		x=1ll*x*x%P;
		y>>=1;
	}
	return ans;
}

inline void init() {
	isp[1]=1;
	phi[1]=1;
	for(int i=2; i<=N; ++i) {
		if(!isp[i]) {
			pri[++tot]=i;
			phi[i]=i-1;
		}
		for(int j=1; i*pri[j]<=N && j<=tot; ++j) {
			isp[i*pri[j]]=1;
			if(i%pri[j]==0) {
				phi[i*pri[j]]=phi[i]*pri[j];
				break;
			}
			phi[i*pri[j]]=phi[i]*phi[pri[j]];
		}
	}
	ans=1;
	for(int i=1; i<=N; ++i) {
		phi[i]=(phi[i-1]+phi[i])%(P-1);
		ans=ans*i%P;
	}
	ans=ksm(ans,2*N);
	return;
}

int main() {
	scanf("%d",&N);
	init();
	ll tmp=1;
	for(int i=1; i<=N; ++i) {
		tmp=tmp*ksm(i,2*phi[N/i]-1)%P;
	}
	tmp=tmp*tmp%P;
	tmp=ksm(tmp,P-2);
	ans=ans*tmp%P;
	printf("%lld\n",ans);
	return 0;
}

P3746 [六省联考2017]组合数问题

组合意义:在nk个本质不同物品中选出t个满足 $mod k=r$

关于这个问题,我们有一个经典解法,就是动态规划

f_{i,k}=f_{i-1,(k-1)mod k}+f_{i-1,k}

就是mod k意义下做...

那你会发现这个东西可以矩阵快速幂优化,于是我们冲一下就做完了

转移矩阵是

101
110
010

初始态是 $f_{0,0}=1$

时间复杂度是 $O(k^3logn)$

code:

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=55;
int n,P,k,r;
inline void add(int &x,int y) {
	x+=y;
	if(x>=P)x-=P;
}
struct mat {
	int a[MAXN][MAXN];
	inline void init() {
		memset(a,0,sizeof(a));
	}
} a,w;

mat operator*(mat a,mat b) {
	mat c;
	c.init();
	for(int i=0; i<=k; ++i) {
		for(int j=0; j<=k; ++j) {
			for(int l=0; l<=k; ++l) {
				add(c.a[i][j],a.a[i][l]*b.a[l][j]%P);
			}
		}
	}
	return c;
}

mat ksm(mat x,int y) {
	mat ans;
	ans.init();
	for(int i=0; i<=k; ++i)ans.a[i][i]=1;
	while(y) {
		if(y&1)ans=ans*x;
		x=x*x;
		y>>=1;
	}
	return ans;
}


signed main() {
	scanf("%lld%lld%lld%lld",&n,&P,&k,&r);
	k--;
	a.init();
	a.a[0][0]=1;
	w.init();
	for(int i=0; i<=k; ++i) {
		w.a[i][i]++;
		w.a[(i+1)%(k+1)][i]++;
	}
	mat qwq=ksm(w,n*(k+1));
	qwq=qwq*a;
	printf("%lld\n",qwq.a[r][0]);
	return 0;
}

小心k=1的时候,整个矩阵是一个2,所以用++

显然应该可以循环卷积优化到 $n^2logn$

P7116 [NOIP2020] 微信步数

zhq神仙秒空气!

首先我们有一个枚举天数的做法,就是每一天轮流走走走,然后不断cut down那些出界的点,本质上相当于计算一天有多少点合法

这样做看上去是 $O(big)$ 的,但是可以过45...

zhq:

然后我们来观察规律,你会发现单独一维拿出来除了第一遍是走到的最大最小范围为 $[l,r]$ 外,之后一定只是向一个方向扩展了!

因为但凡向两个方向扩展,那你为啥第一遍做的时候走不到啊??

于是我们再仔细把每天计算贡献的式子展开来有
eg:

$A*B+(A-1)*B+(A-1)*(B-1)+(A-1)*(B-2)....$

共n项,而第二次走的时候

$(A-a)*(B-b)+(A-a)*(B-b)+(A-a)*(B-b)+(A-a)*(B-b-1)....$

哇偶

好像完蛋了,但是第三次走的时候

$(A-2a)*(B-2b)+(A-2a)*(B-2b)+(A-2a)*(B-2b)+(A-2a)*(B-2b-1)....$

也就是说,除去第一次,之后的贡献多项式都只和天数有关!

也就是说,如果我们把他写成多项式

$(A-xa)*(B-xb)+(A-xa)*(B-xb)+(A-xa)*(B-xb)+(A-xa)*(B-xb-1)....$

然后乘法展开后就是撑死维度项的!

于是我们可以发现,一旦有一维减到0了就没了,所以我们到减到0之前一轮特判一下即可

然后你会发现假设是x轮,每一个k次方上就是1^k+2k+3^k.....

最后这就是一个自然数幂之和,直接冲就做完了

多项式乘法可以暴力展开(也只能暴力展开)

P5179 Fraction

传说中的sooke三题第三题

看上去就是傻掉,这这这....

分类讨论第一名

$\lceil \frac{a}{b}\rceil<=\lfloor\frac{c}{d}\rfloor$

说明中间存在一个整数,分子就是那个整数,分母是1

说明我们要枚举一个分母k,满足 $1/k<c/d$

有 $\frac{d-ck}{kd}<0$

有 $d<ck$

即 $k>d/c$

$k>\lfloor \frac{d}{c}\rfloor$

其+1就是k吧

$a>=b$

此时我们要注意a可以对b取模啦,根据类欧相关

$\frac{a mod b}{b}<ans-\lfloor\frac{a}{b}\rfloor<c/d-\lfloor\frac{a}{b}\rfloor$

于是只需要将p加上 $q*\lfloor\frac{a}{b}\rfloor$

将 $c-d*\lfloor\frac{a}{b}\rfloor$

$a<=b && c<=d$

优化枚举的过程?

啊,我们可以每个数都取倒数,然后就变成了大于的情况,等等倒数?

所以是

\frac{d}{c}<\frac{q}{p}<\frac{b}{a}

根据题目中给出的性质,不可能有分数 $a<=b$ 但 $c>=d$ 不被边界1判掉的,不可能有分数不属于这四种case

做完了,直到边界1,2为止qwq

注意运算优先级,以及EOF

code:

#include<bits/stdc++.h>
#define ll long long
#define db double
using namespace std;

ll a, b, c, d, p, q;

inline void solve(ll a, ll b, ll c, ll d, ll &p, ll &q) {
	if(a / b + 1 <= ceil(c / (db)d) - 1) {
		p = a / b + 1;
		q = 1;
		return;
	}
	if(a == 0) {
		p = 1;
		q = d / c + 1;
		return ;
	}

	// printf("%lld %lld %lld %lld\n", a, b, c, d);
	if(a <= b && c <= d) {
		solve(d, c, b, a, q, p);
		return ;
	}
	solve(a % b, b, c - (a / b) * d, d, p, q);
	p += q * (a / b);
	return;
}

int main() {
	while(scanf("%lld%lld%lld%lld", &a, &b, &c, &d) != EOF) {
		solve(a, b, c, d, p, q);
		printf("%lld/%lld\n", p, q);
	}
	return 0;
}

P6156 简单题

\sum_{i=1}^n\sum_{j=1}^n(i+j)^kf_{gcd(i,j)}gcd_(i,j)

经过一点简单的反演我们得到

\sum_{T=1}^n T^k \sum_{d|T}d^{k+1} \mu{d}^2 \mu{T/d} S_{\frac{n}{T}}

S(n)=\sum_{i=1}^n\sum_{j=1}^n (i+j)^k

考虑观察一下,相当于所有i=1~n的被算了i-1次,然后i+1到2n的被算了2n-i次

设

f_n=\sum_{i=1}^n i^k

这个等价于

\sum_{i=n+1}^{2n}f_i - \sum_{i=1}^n f_i

于是我们处理sum表示 $f_i$ 的前缀和即可,同时k次幂可以线性筛 $O(n/logn*logk)$ ,然后f就把这个k次幂求和即可

~~确实很妙~~

T^k \sum_{d|T}d^{k+1} \mu{d}^2 \mu{T/d}

然后我们再考虑那个前面要筛出来的那个东西...., $p^k$ 为其最小的质因子指数

f_x=f_{p^k}*f_{x/p^k}

有个新方法,就是枚举一下取值,枚举一下k值

k=0,此时x=1, $f_x=1$

k=1,此时 $f_p=p-1$ ,显然带入即可

k=2,此时 $f_{p^2}=-p$ ,显然带入即可,有1的系数为0,p的系数为-1, $p^2$ 的系数为0

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int P = 998244353;
const int MAXN = 1e7 + 2e6 + 7;
int n, tot;
int f[MAXN], isp[MAXN], pri[MAXN];
ll S[MAXN], g[MAXN], k; //g是即兴函数

inline ll ksm(ll x, ll y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

inline void add(ll &x, ll y) {
	x += y;
	if(x >= P)x -= P;
}

inline void add(int &x, ll y) {
	x += y;
	if(x >= P)x -= P;
}

inline void init() {
	f[1] = 1;
	g[1] = 1;
	for(int i = 2; i <= 2 * n; ++i) {
		if(!isp[i]) {
			pri[++tot] = i;
			f[i] = i - 1;
			g[i] = ksm(i, k);
			// printf("%d %lld %lld?\n", i, g[i], f[i]);
		}
		for(int j = 1; j <= tot && i * pri[j] <= 2 * n; ++j) {
			isp[i * pri[j]] = 1;
			g[i * pri[j]] = g[i] * g[pri[j]] % P;
			if(i % pri[j] == 0) {
				int q = i / pri[j];
				if(q % pri[j])f[i * pri[j]] = 1ll * (P - pri[j]) * f[q] % P;
				break;
			}
			f[i * pri[j]] = 1ll * f[i] * (pri[j] - 1) % P;
		}
	}
	for(int i = 1; i <= 2 * n; ++i) {
		f[i] = 1ll * f[i] * g[i] % P;
		add(f[i], f[i - 1] % P);
		add(g[i], g[i - 1]);
	}
	for(int i = 1; i <= 2 * n; ++i) {
		add(g[i], g[i - 1]);
	}
	return;
}


inline ll calc(int x) {
	return (g[x << 1] - 2 * g[x] % P + P) % P;
}

int main() {
	scanf("%d%lld", &n, &k);
	init();
	ll ans = 0;
	for(int l = 1, r; l <= n; l = r + 1) {
		r = n / (n / l);
		ans = (ans + 1ll * ((f[r] - f[l - 1] + P) % P) * calc(n / l) % P) % P;
	}
	printf("%lld\n", ans);
	return 0;
}

P4619 [SDOI2018]旧试题

超级神仙题

首先反演部分，我们要考虑约数个数这个东西可以转换成所有数的互质因数pair个数

因为考虑三个数的LCM，他们可能会被算重好多次，但是其中一定有一个是三个互质的数凑出的，单凡三个数不互质，我们可以让其中拥有公共部分的数去掉这个公共部分，剩下的仍然是约数

另外三个互质的数只可能有唯一的LCM，同时一个LCM可能不由唯一的三个互质的数凑出来，但如果不是唯一的，我们可以发现类似于分配一下算重的部分的编号，使得他们表示了每一个更大的LCM数

eg：3,5,7，其中5A,B都有，那么我们

35 7 表示357

3 57 表示355*7即可

而这个情况很唯一，如果有两个以上的因子，想一想就只能是直接分配了，（左边i个右边0个）然后正好把i+j+1个指数记了i+j+1次

\sum_{i=1}^{A}\sum_{j=1}^{B}\sum_{k=1}^{C}\sigma_{0}(ijk)

\sum_{i=1}^{A}\sum_{j=1}^{B}\sum_{k=1}^{C}\sum_{d|i}\sum_{t|j}\sum_{p|k}\epsilon((d,t))\epsilon((t,p))\epsilon((d,p))

交换

\sum_{i=1}^{A}\sum_{d|i}\sum_{j=1}^{B}\sum_{t|j}\sum_{k=1}^{C}\sum_{p|k}\epsilon((d,t))\epsilon((t,p))\epsilon((d,p))

\sum_{d=1}^{A}\lfloor\frac{A}{d}\rfloor\sum_{t=1}^{B}\lfloor\frac{B}{t}\rfloor\sum_{p=1}^{C}\lfloor\frac{C}{p}\rfloor\epsilon((d,t))\epsilon((t,p))\epsilon((d,p))

\sum_{d=1}^{A}\sum_{t=1}^{B}\sum_{p=1}^{C}\lfloor\frac{A}{d}\rfloor\lfloor\frac{B}{t}\rfloor\lfloor\frac{C}{p}\rfloor\sum_{u|t\&u|d}\mu(u)\sum_{v|t\&v|p}\mu(v)\sum_{w|d\&w|p}\mu(w)

qwq交换求和符号？？

你仔细想想发现我们还是可以搞出LCM，但是要是两两的。。。

\sum_{u=1}^{minA,B}\sum_{v=1}^{minB,C}\sum_{w=1}^{minA,C}\sum_{u|t\&u|d}\lfloor\frac{A}{d}\rfloor\mu(u)\sum_{v|t\&v|p}\mu(v)\lfloor\frac{B}{t}\rfloor\sum_{w|d\&w|p}\mu(w)\lfloor\frac{C}{p}\rfloor

然后用LCM代替

f_x(z)=\sum_{y|x}\lfloor\frac{z}{y}\rfloor

\sum_{u=1}^{min(A,B)}\sum_{v=1}^{min(B,C)}\sum_{w=1}^{min(A,C)}\mu(u)\mu(v)\mu(w)f(lcm(u,w),A)f(lcm(u,v),B)f(lcm(v,w),C)

然后我们开始三元环计数

然后发现不能连边哎,加速一下:

下面我们从1到 $max(A,B,C)$ 枚举边权i，首先因为这个边权是两个 $\mu$ 值不为0 的数的 $lcm$ ，因此 $\mu(i)!=0$ ，下面我们直接 $2^k$ 的枚举这个i的质因数分解集合的一个子集，由这个子集我们可以得到其中的一个点的编号u，之后我们要确定另外一个点v但是我们发现v不是非常的好枚举了，因此我们可以枚 $gcd(u,v)$ 显然这个gcd一定是u对应的集合的子集，因此我们再次枚举u的子集确定出gcd，那么对应的v就是 $i×gcd/u$ 了之后我们就在u和v间连一条边

建完图之后,使用三元环计数即可,因为我们已经能找到三元环了,所以给边分配相应的编号也并不困难

时间复杂度 $O(m\sqrt m)$

本题要卡常,用vector存图降低cache miss

P2624 [HNOI2008]明明的烦恼

有根树我会枚举根是谁然后直接在fa序列上计数

无根树就只能prufer序列了,一个度数为i的点出现在prufer序列中i-1次

考虑之前已经固定度数的颜色,把他们度数-1后,相当于一个组合数连乘

$C_{n,i}*C_{n-i,j}*C_{n-i-j,k}...$

然后之后没有固定度数的,可以填剩下的位置,并且每个位置都有 $n-cnt-2$ 种方法,次方一下就好了

P6271 [湖北省队互测2014]一个人的数论

求

\sum_{i=1}^n[gcd(i,n)==1]i^k

n<=1000000000^{{1000000000}^{1000}}

n<=1e9

\sum_{d|n}\mu (d) d^k \sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}i^k

显然我们没有这个d^k的

\sum_{d|n}\mu (d) \lfloor\frac{n}{d}\rfloor

那么我们就做完了,直接dp这个系数,因为取值只有 $p_i$ 和1,不对,可以

\prod_{p|n}(1-p) \lfloor\frac{n}{p}\rfloor

这个生成函数还是可爱的

上述有40分!

\sum_{d|n}\mu (d) d^k \sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}i^k

根据伯努利数,有限微积分,或者斯特林数我们可以知道这个是关于次数的一个多项式, $f_i$ 表示多项式第i项系数

\sum_{d|n}\mu (d) d^k \sum_{i=0}^{k+1}f_i(\frac{n}{d})^i

\sum_{i=0}^{k+1}f_i n^i \sum_{d|n}\mu (d) d^{k-i}

观察后面那个东西,显然由mu的取值可以有

\sum_{i=0}^{k+1}f_i n^i \prod_{P_j|n}(1-P_j^{k-i})

拉格朗日插值出这个多项式每个系数?这个可以做到 $O(n^2)$ ,但是高斯消元他不香吗?


#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 2000;
const int P = 1e9 + 7;
int K, m, p[MAXN], a[MAXN];
ll tmpx[MAXN], tmpy[MAXN], n;
ll G[MAXN], F[MAXN], H[MAXN], Q[MAXN];

inline ll ksm(ll x, ll y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

inline void init(int n) {//预处理自然幂数和多项式系数
	G[0] = 1;
	for(int i = 1; i <= n + 2; ++i) {//n+2个点值
		tmpx[i] = i;
		tmpy[i] = 0;
		for(int j = i; j >= 1; --j) {//n+2次多项式G
			G[j] = (G[j - 1] - G[j] * tmpx[i] % P + P) % P;
			tmpy[i] += ksm(j, n);//n次幂和,n+1次多项式
			tmpy[i] %= P;
		}
		G[0] = (-G[0] * tmpx[i] % P + P) % P;
		// printf("%lld %lld\n", tmpx[i], tmpy[i]);
	}
	// for(int i = 0; i <= n + 3; ++i)printf("%lld ", G[i]);
	// puts("");
	for(int i = 1; i <= n + 2; ++i) {
		ll tmpg = 1;
		for(int j = 1; j <= n + 2; ++j) {
			if(i != j) {
				tmpg = tmpg * (tmpx[i] - tmpx[j] + P) % P;
			}
		}
		tmpg = ksm(tmpg, P - 2);

		for(int j = n + 2; j >= 0; --j)Q[j] = G[j];
		for(int j = n + 2; j >= 1; --j) {
			H[j - 1] = Q[j];
			Q[j - 1] += Q[j] * tmpx[i] % P;
		}

		for(int j = n + 1; j >= 0; --j)
			F[j] = (F[j] + H[j] * tmpy[i] % P * tmpg % P) % P;
	}
	// for(int i = 0; i <= n + 1; ++i)printf("%lld ", F[i]);
	return ;
}

int main() {
	scanf("%d%d", &K, &m);
	n = 1;
	for(int i = 1; i <= m; ++i) {
		scanf("%d%d", &p[i], &a[i]);
		n = ksm(p[i], a[i]) * n % P;
	}
	init(K);
	ll ans = 0;
	for(int i = 0; i <= K + 1; ++i) {
		ll tmpg = 1;
		for(int j = 1; j <= m; ++j) {
			tmpg = tmpg * (P - ksm(p[j], K - i + P - 1) + 1) % P;
		}
		ans += tmpg * F[i] % P * ksm(n, i) % P;
		ans %= P;
	}
	printf("%lld\n", ans);
	return 0;
}

夏晓光(loveJY)的博客

贝尔的数学篇

二次剩余

勒让德符号

欧拉判别准则

Cipolla 算法

P5491 【模板】二次剩余

类欧几里得算法

P5171 Earthquake

P5172 Sum

P5221 Product

P3746 [六省联考2017]组合数问题

P7116 [NOIP2020] 微信步数

P5179 Fraction

P6156 简单题

P4619 [SDOI2018]旧试题

P2624 [HNOI2008]明明的烦恼

P6271 [湖北省队互测2014]一个人的数论

昴的博弈论2