「C.E.L.U」Round1

难度有点梯度...

obviously,要么奇数为负要么偶数为负

求最大子段和

O(n)搜索一下

考虑u是第i层的祖先,j能否为第i+1层的祖先

有两种方法:

考虑第k+1层的祖先一定不会在u之上,而最大深度要达到dep+1才能是dep+1的祖先

而不仅如此,还要满足一个儿子v是dep+1最大深度,其他的儿子最大深度都不能是dep+1才行

所以说满足这个条件我们就可以向下递归

预处理深度最大深度即可

预处理同一深度最大dfn序和最小的

然后直到子树的siz,可以求出子树dfn范围

如果包括了最大最小的就继续向下走这样子

毒瘤

介绍一下这个题所用的冷门算法：矩形切割。

矩形切割，就是将它有相交部分的矩形分割成若干个小矩形，从而消除重叠的部分，方便计算面积。当然，其它维度也是一样的。由于每次插入和查询时都要遍历一遍已经存在的所有矩形，所有时间复杂度是 $\text{O}(n^2k\sim n^3k)$ 的。常数与维度和矩形密集程度有关，且较大。
为了方便，就以二维的情况为进行一次模拟操作，其它维度也是一个道理。
假设这里有一个矩形 A 和一个矩形 B，它们是相交的（不相交的情况直接忽略）

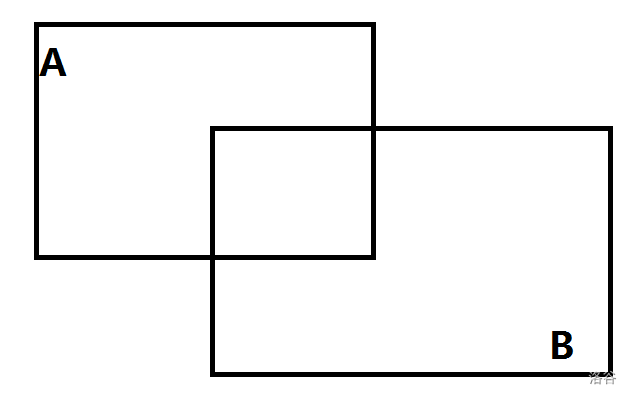
所谓的矩形切割，就是删除原来的 A，替换成全新的 A1 和 A2，这样，每一个矩形之间就没有相交的部分，所以计算面积就可以直接把所有的矩形的面积加起来，就可以得到答案。

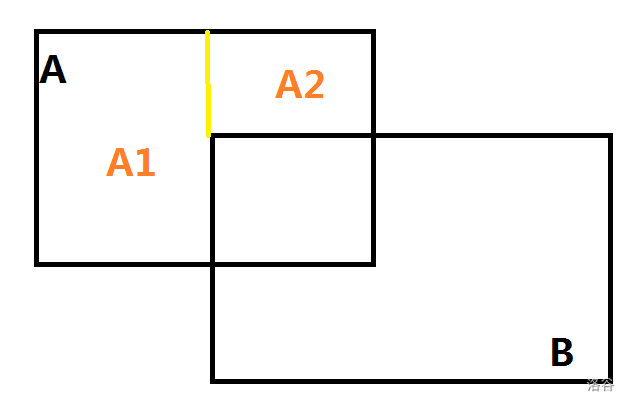
(实际上就是每一维都弄一下的样子)

考虑一个连通块一个连通块的转移

f_S表示S集合内的点已经考虑,其他点还没有考虑的期望值

就是枚举子集进行转移,然后加上另一个的期望值

然后会发现我们要转移一个子集的内部连通的概率....

这个可以容斥,就是考虑这个子集的子集单独连通,另外的一部分不向外界连边即可

code:


#include<bits/stdc++.h>
#define db double
using namespace std;
const int maxn = 5005;
db dp[maxn];
db a[15][15];
db cte[maxn];
int n, mS;
int lowbit(int x) {
   int cnt = 0;
   while(x) {
   	if(x & 1) cnt ++;
   	x >>= 1;
   }
   return cnt;
}
db calc(int x) {
   db ans = 1.0;
   for(int i = 1; i <= n; ++i)for(int j = i + 1; j <= n; ++j)if(((x >> i - 1) & 1) ^ ((x >> j - 1) & 1))ans *= (1 - a[i][j]);
   return ans;
}

db calc2(int x, int y) {
   db ans = 1.0;
   for(int i = 1; i <= n; ++i)for(int j = 1; j <= n; ++j)if(((x >> i - 1) & 1) && ((y >> j - 1) & 1))ans *= (1 - a[i][j]);
   return ans;
}

int lowbit2(int x) {
   return x & (-x);
}

void init() {
   for(int S = 1; S <= mS; ++S) {
   	if(lowbit(S) == 1) {
   		cte[S] = calc(S);
   		continue;
   	}
   	int g = lowbit2(S);
   	int T = S ^ g;
   	for(int j = T; j != -1; j = (j - 1)&T) {
   		if(j == T) {
   			cte[S] += calc(S);
   			continue;
   		}
   		cte[S] -= cte[j | g] * calc2(S ^ (j | g), mS ^ S);
   		if(j == 0) break;
   	}
   }
}

int main() {
   scanf("%d", &n);
   for(int i = 1; i <= n; ++i) {
   	for(int j = 1; j <= n; ++j)
   		scanf("%lf", &a[i][j]);
   }
   mS = (1 << n) - 1;
   init();
   for(int S = 0; S < 1 << n; ++S) {
   	int T = mS ^ S;
   	for(int T2 = T; T2; T2 = (T2 - 1)&S) {
   		dp[S | T2] += dp[S] + cte[T2];
   	}
   }
   printf("%.6lf", dp[mS]);
   return 0;
}

夏晓光(loveJY)的博客

NOIP提高组考前刷题冲刺班（第一场）