CF1404A Balanced Bitstring

巧妙啊!!!

构造题...

我们要满足这个条件就是

$\sum_{i=0}^ka_{p+i}=\frac{k}{2}$

又有

$\sum_{i=1}^{k+1}a_{p+i}=\frac{p}{2}$

就有$a_{k+1}=a_1$

有了这个结论我们就知道所有%k同余的位置字符相同

然后对于剩下的限制,我们可以任意调整每个cnt的取值,也就是说1的数量或者0的数量都不能超过cnt

CF1404B Tree Tag

分类讨论题,一共有三种情况

要么Alice能够把bob逼到死角(大于等于他移动的两倍),要么Alice能开局就赢,要么Alice能占据整颗树

CF1404C Fixed Point Removal

$b_i$表示要删除这个数前面至少要删除多少数

这个不难发现是$i-a_i$,如果$a_i<i$就是不可能的...

那么我们就是查询区间0,1,2,3最长子序列的信息

所有数都先固定,然后从前向后加入可以操作的数,对于加入数x,我们不能发现可以从最近的合法的$x-1$元素转移而来

然后查询就等价于最大的合法元素满足$pre$大于等于这个L,同时坐标要落在这个范围内,这个可能很二维偏序QAQ,离线一下就好了

题解告诉我们后面的数不会对前面产生影响

因此可以从后向前处理,每次删掉一个为0的数,把后面没有删掉的数统一减一,变成0就连锁反应一下

然后就相当于对于一个左端点,回答所有被删掉的右端点的前的最大值

P6062 [USACO05JAN]Muddy Fields G

每个奶牛要么被横着的木板覆盖,要么被竖着的木板覆盖

所有横的和所有竖的木板拿出来建点,于是对于一个点相对应的两侧连边

然后你发现它等价于最小点覆盖我忘了/ll,就等于最大匹配

跑网络流即可

CF1404E Bricks

之前的题和这道题做法不一样好吗....

本题的核心思想是用网络流实现连边合并的过程

一开始我们用$1*1$放满整张图

然后对于相邻两个黑色节点的边$(x,y)$,我们认为他如果选上,相当于延伸了一个矩形,减少了答案

那么我们要选出尽量多的边,同时不会出现矩形变成L形的情况,把这样的边转成点

这告诉我们下图中黄色的边连边的点不能同时选

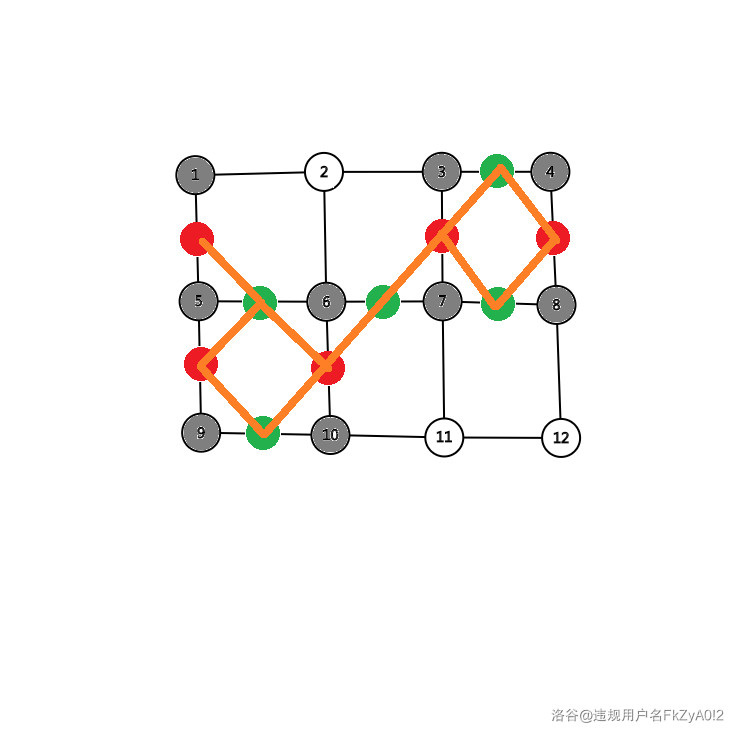
于是就和二分图最大独立集就是一样的了,直接最大独立集即可,等于点数-最小点覆盖

答案就是总黑格数-(点数-最大匹配)

P3967 [TJOI2014]匹配

链接题

一定在最大费用流里的边一定不可能是第一次流完之后不再最大费用流里面的边,剩下的就随便删一下

然后就被EI哥哥教育了

这个相当于建立零环的DAG,然后从两端点$(u,v)$u向v跑一遍最大流,如果跑出的最大流能大于这条边流量则说明可行

零环是什么?就是费用和在加势意义下为0的一个环,或者说是对于(u,v)这条边费用和完全和其相同的环,因为但凡比(u,v)贵我们不可能采用,否则必(u,v)便宜我们一定已经采用,这样的环是(u,v)的一个完全可等价替代的路径

这些环构成的是DAG,那么对于这些DAG我们跑最大流即可

给定一个两侧各有n和m个点的二分图（保证$n\leq m$），对于每条边，你需要判断原图是否存在一个大小为n，且包含了这条边的匹配。

如果n=m,那么还是可以发现我们把非匹配边从第二排点向第一排点连边,然后匹配点从第一排点向第二排点连边

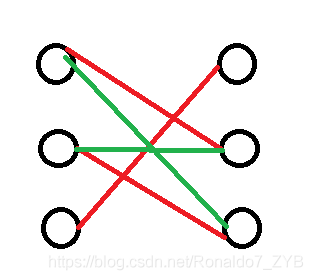
原理就是这里面一个圈的边可以轮换匹配边

然后求强联通分量,就能知道如果一条边两个点都在一个连通分量就是可以在最大匹配里的

$n<m$?

一个虚拟点用匹配边右边点连他用它连接非匹配左边点

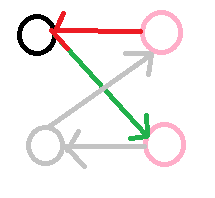
这样，我们可以得到一个方案是匹配边，虚边，虚边和非匹配边；倒过来就是非匹配边，虚边，虚边和匹配边；那么，我们倒过来就可以得到一组合法的方案。

这个虚拟点之间不要连边,如果左边点多就把所有虚拟点强制令右边补齐匹配,就是和右边所有点连边