夏晓光(loveJY)的博客

仍要向下扎根,向上结果

首页 归档 标签 关于 友链

CF506E Mr. Kitayuta's Gift

2020-03-16 14 min read # 矩阵乘法 # 专属标签:压缩自动机 # 字符串 # 集训队作业 # 动态规划

IOI2020集训队作业

集训队作业(或者说CF)终于展现出他可怕的一面

  • 给定一个小写字符串 ss 和一个正整数 nn。
  • 要求在 ss 中插入恰好 nn 个小写字符使其回文的方案数。
  • ∣s∣≤200|s| \le 200，n≤109n \le 10^9，答案对 104+710^4 + 7 取模。

首先这道题肯定是要DP的,然而这个n实在不敢恭维,模数大小也一般没用

题目变成长度为|S|+n的所有字符串包含|S|为子序列的有多少个

我们仿照一般的对字符串进行dp的套路,我们不停的一位一位的放字符来进行决策,换句话讲我们的转移就是枚举下一位放什么,这样dp有一个相当棒的好处就是我们永远不会重复数同一个串

先从DP入手吧,经典字符串DP套路,dp[i][j][k]dp[i][j][k]表示S字符串从i->j没有匹配,当前字符串从前数k个位置到从后数k个位置已经匹配,注意,S是当前字符串的一个子序列,的方案数

另设target(k)表示前k位和后k为已经确定时包含包含S这个子序列的字符串数

转移就是头尾同时添加一个字符,因为如果状态设计或转移的不好就可能将一个串多次计数了

所以我们采取这样一种策略匹配子序列从头尾两端同时添加字符,一旦可以和$S$匹配子序列就进行匹配,可以证明的是如果这个字符串含有子序列$S$就肯定能被这个算法识别出一个子序列来，并且我们还可以证明的是对于同一个字符串被识别出的子序列有且仅有一种,因此我们会发现这样设计状态的话每个字符串就只会被统计一次了,所以我们的"还没有匹配的区间"指的就是这样贪心的匹配完前后$k$位之后

然后具体的....先考虑偶长度字符串吧,显然j>=ij>=i

case 1:S[i]==S[j]&&j-i<=1

我们再放一个S(i)就拼完了,另外我们还可以瞎放,但只能使匹配k+1

target(k+1)+=dp[i][j][k]target(k+1)+=dp[i][j][k]

dp[i][j][k+1]+=dp[i][j][k]∗25dp[i][j][k+1]+=dp[i][j][k]*25

case2:S[i]==S[j]&&j-i>1

仿照上面的吧,target无法更新,我们可以一下匹配S两个位置,也可以k+1

dp[i][j][k+1]+=dp[i][j][k]∗25dp[i][j][k+1]+=dp[i][j][k]*25

dp[i+1][j−1][k+1]+=dp[i][j][k]dp[i+1][j-1][k+1]+=dp[i][j][k]

case3:S[i]!=S[j]S[i]!=S[j]

我们只能选择其中一方匹配,或者k+1

dp[i+1][j][k+1]+=dp[i][j][k]dp[i+1][j][k+1]+=dp[i][j][k]

dp[i][j−1][k+1]+=dp[i][j][k]dp[i][j-1][k+1]+=dp[i][j][k]

dp[i][j][k+1]+=dp[i][j][k]∗24dp[i][j][k+1]+=dp[i][j][k]*24

case4:target

显然target可以随便填

target(k+1)+=26∗target(k)target(k+1)+=26*target(k)

那么显然我们只需要target((∣S∣+n)/2)target((|S|+n)/2)的值就是答案了,发现每次都从k->k+1,那么k不用计入状态中可以直接矩阵乘法,这样我们矩阵至少要记录∣S∣4|S|^4大小的信息,O(∣S∣6log(∣S∣+n))O(|S|^6log(|S|+n))

不行,我们来优化一下,明显我们有一个浪费,就是只需要target一项的值,所以我们要像个办法利用起来

考虑DP的本质其实是一个DAG上图论?所以如果状态A到状态B有

dp(A)+=C∗dp(B)dp(A)+=C*dp(B)

就在点B向点A连C条有向边,(如果只有k值不同我们看做相同的状态哦)

那么显然去掉一些自环就是DAG了!那么问题也相对的转化一下,变为(1,n)(1,n)这个点到target((∣S∣+n)/2)target((|S|+n)/2)走(∣S∣+n)/2(|S|+n)/2条边路径方案总数

很好,问题变成图的路径计数了!

但首先要解决自环,自环只有24,25,26三种呢

这又有什么用处呢?我们仔细观察图上每一条路径,大部分的时间我们都在走自环了!经过的点的种类却很少,最多经过∣S∣|S|个点,这个观察状态转移方程不难得出

那我们把路径按照经过点的点集分类,一类路径就是走相同的点集到终点的路径,那么一类路径中不同的路径就一定是走自环的方式不同了

其中26的限制只有在终点上有,我们只需要暴力乘进去就行了

而24和25的点呢?我们发现一个性质,如果已知一条路径(经过的点写成序列)有a个自环数为24的点,那么一定有经过自环数为25的点⌈n−a2⌉\lceil{\frac{n-a}{2}}\rceil,这个可以由DP转移特性得出,因为我们走环为24的点时就消耗一个字符,而走自环为25的点消耗两个字符,又因为我们只走这两种点,所以可以,为什么上取整呢?因为经过(i,i)(i,i)时环长25但是只花了1个字符呢

这个性质告诉我们什么?本质不同的路径条数只有O(|S|)种!!!因为只有包含自环24的点数量不同的路径才本质不同,否则一定相同,因为自环25的点数可以推出来

考虑原图的自动机是不是就可以压缩了?

原来是一个复杂的图,可能长这样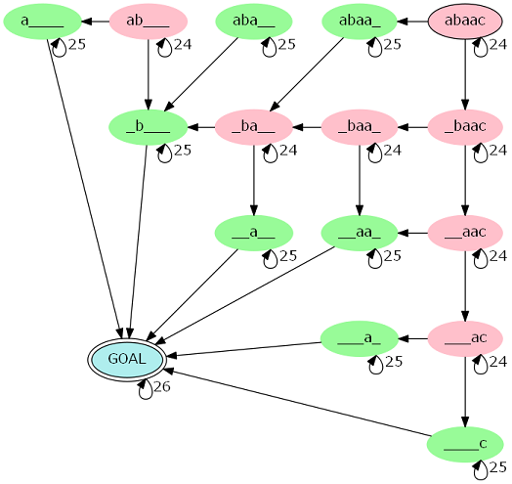qwq

然而我们只需要自环24的点不同,求这些路径本质不同方案数,所以可以压缩为
qwq

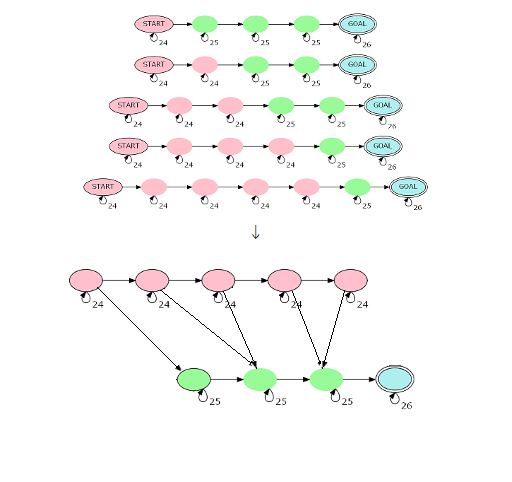
在这上面矩阵乘法

当然,我们还需要求出有k个红点链的总数量,这个只要在原图中用记忆化搜索处理一下即可O(∣S∣3)O(|S|^3)

|S|条链,每个链|S|个点,这个过程不难发现是O(∣S∣4log...)O(|S|^4log...)

显然照T不误,我们再考虑优化一下,因为我们有一个O(|S|^2)大小矩阵但是只用其中的一个数...

矩阵乘法其实支持多个源点和汇点的,C(i,j)C(i,j)就表示从i走到j的方案数呢,所以我们要尽可能的利用一个矩阵内的信息,怎么办?重构图让他满足

所以我们再把自动机压缩一下!!!qaq

这一步我们会发现原来每类链都能在这个图中表示出来!压缩后的自动机点数就只有O(∣S∣)O(|S|)个了.......这时候再次矩阵快速幂,就有O(∣S∣3log(n+S))O(|S|^3log(n+S))

自己核算一下,还是过不了的,毕竟100w*30....

那么我们只需要卡常就行了!让他跑不满!!

我们设计图的时候只让编号小的向编号大的点转移,这样矩阵乘法只需要一个上三角矩阵,这样矩阵乘法的复杂度就除了6,看上去可过

奇数长度串处理方式

唯一的区别好像是case1,j-i=1的时候不能一下转移完了,所以要剪掉这些部分,就只保留这样的链,同时去掉终点自环(因为他只能填中间固定的那个字符了),再算一下就是我们要去掉的方案数了

而其他状态都可以中心字符随便搞

就这样,这道神仙题完了

code:


#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=2*1e2+10;
const int P=10007;
int tr[MAXN][MAXN];
int tp[MAXN*MAXN];
int n;
char mde[MAXN];
int m,ctt,S,ans;
int trp[MAXN<<1][MAXN<<1];
struct Grph {
	int to[2*MAXN*MAXN];
	int nxt[2*MAXN*MAXN];
	int ccnt;
	int home[MAXN*MAXN],dp[MAXN][MAXN*MAXN];
	bool book[MAXN][MAXN*MAXN];
	inline void add(int u,int v) {
		to[++ccnt]=v;
		nxt[ccnt]=home[u];
		home[u]=ccnt;
	}
	inline int dfs(int cnt,int u) {
		if(cnt<0)return 0;
		if(book[cnt][u])return dp[cnt][u];//记忆化搜索
		book[cnt][u]=1;//这个状态算过了
		for(int i=home[u]; i; i=nxt[i])(dp[cnt][u]+=dfs(cnt-tp[u],to[i]))%=P;//加上
		return dp[cnt][u];
	}
} g2;

struct mar {
	int mp[MAXN<<1][MAXN<<1];
	inline int* operator[](const int x) {
		return mp[x];
	}
	void operator*=(const mar &b) {
		for(int i=1; i<=S; ++i)
			for(int j=1; j<=S; ++j)trp[i][j]=0;
		for(int i=1; i<=S; ++i)
			for(int k=i; k<=S; ++k)
				for(int j=k; j<=S; ++j)
					(trp[i][j]+=mp[i][k]*b.mp[k][j])%=P;
		for(int i=1; i<=S; ++i)
			for(int j=1; j<=S; ++j)mp[i][j]=trp[i][j];
	}
} trs,res;


int f[MAXN],g[MAXN];
int main() {
	scanf("%s",mde+1);
	scanf("%d",&m);
	for(n=1; mde[n+1]!='\0'; ++n);
	for(int i=1; i<=n; ++i)
		for(int j=i; j<=n; ++j)
			tr[i][j]=++ctt;//这里原来是重编号,保证了从编号小的向编号大的转移
	++ctt;
	for(int i=1; i<=n; ++i) {
		for(int j=i; j<=n; ++j) {
			if(mde[i]==mde[j]) {
				if(j-i<=1)g2.add(ctt,tr[i][j]);//只连一条边

				else g2.add(tr[i+1][j-1],tr[i][j]);//否则从i+1,j-1可以转移到i,j
			} else {
				tp[tr[i][j]]=1;//这个东西

				g2.add(tr[i+1][j],tr[i][j]),g2.add(tr[i][j-1],tr[i][j]);
				//先构建原图来记搜
			}
		}
	}
	for(int i=0; i<n; ++i)g2.book[i][tr[1][n]]=1;
	g2.dp[tp[tr[1][n]]][tr[1][n]]=1;
	//靠,这是设计初状态.....
	for(int i=0; i<n; ++i)g2.dfs(i,ctt);
	//记忆化搜索每个填的
	for(int i=1; i<n; ++i)trs[i][i]=24;
	//这些点只可24
	int t=(n+1)/2;
	for(int i=0; i<t; ++i)trs[i+n][n+i]=25;
	//这些点是25
	for(int i=0; i<t; ++i)trs[n+t+i][n+t+i]=26;
	//终点
	for(int i=1; i<n+t-1; ++i)trs[i][i+1]++;
	//你想像一下之前的那个两条链的图第一条链相邻点的边
	for(int i=0; i<t; ++i)trs[n+i][n+t+i]++;
	//这个是第二条链的对应边
//	for(int i=0; i<n; ++i) {
//		for(int j=0; j<n; ++j) {
//			printf("%d ",trs[i][j]);
//		}
//		puts("");
//	}
	S=n+(t<<1)-1;
	for(int i=1; i<=S; ++i)res[i][i]=1;
	//单位矩阵
	for(int p=(n+m)>>1; p; p>>=1,trs*=trs)if(p&1)res*=trs;//靠,快速幂

	for(int i=0,v; i<n; ++i)v=(n-i+1)/2,f[i]=res[n-i][n+t+v-1],g[i]=res[n-i][n+v-1];//这个g其实是最后到单个字符的 
	//这是在枚举所有路径类,然后得到对应
	if((n+m)&1) {
		for(int i=0; i<n; ++i)(ans+=f[i]*g2.dp[i][ctt])%=P;//路径类*路径条,ctt是重点 
		(ans*=26)%=P;//终点的自环
		for(int i=1; i<=26; ++i) {
			for(int j=1; j<=n; ++j) {//枚举最后是啥
				if(mde[j]=='a'+i-1)//如果这个可以做最后
					for(int k=0; k<n; ++k)(ans+=g[k]*g2.dp[k][tr[j][j]])%=P;//再加上到这个单个字符点可以的 
			}
		}
	} else {
		for(int i=0; i<n; ++i)(ans+=f[i]*g2.dp[i][ctt])%=P;
	}
	printf("%d",ans);
	return 0;
}
Powered by Gridea RSS