CF516E Drazil and His Happy Friends

IOI2020集训队作业

果然集训队作业里面什么都有啊qwq

有 $n$ 个男生 $m$ 个女生，编号分别为 $0 \sim n - 1$ 和 $0 \sim m - 1$ 。
有 $b$ 个男生和 $g$ 个女生是快乐的，其他人是不快乐的。
在第 $i$ 天，编号为 $i \bmod n$ 的男生和编号为 $i \bmod m$ 的女生会一起玩。
如果他们俩中有一个人是快乐的，则另一个人也会变快乐。
求至少要多少天所有人都会变快乐，或者判断不可能所有人都变快乐。
$n,m \le 10^9$ ， $b,g \le 10^5$ 。

看上去很可以暴力的样子,然而这个题是CF题,没有部分分....

我们首先想错位对齐有哪些数永远对不上...

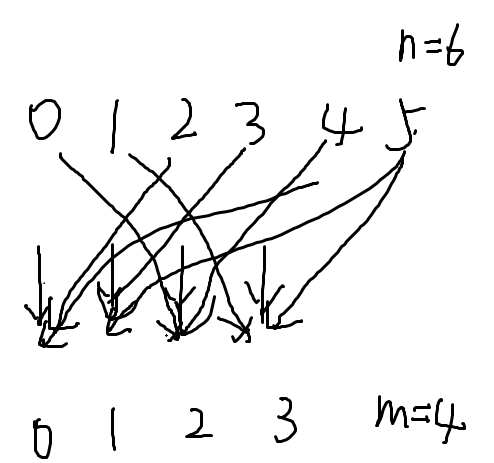
发现可以mod gcd分组,同一组内至少要有一个1,这样至少在n*m天后能全开心,否则无解啊

所以只需要每一组答案求出来取个max就行

假设n>m,且gcd(n,m)=1

那么如果有n个男生快乐了,除非天数小于m,所有的女生也一定快乐了,这是因为女生每天都至少被多影响一个人

所以我们只需要求出最后一个变快乐男生的时间,假定如果初始时女生快乐对应男生也快乐

那么一个男生x在t天变快乐了,就可以再经过m轮让使他变快乐的那个女生把 $(t+m)\bmod n$ 男生也快乐了

这个相当于同余最短路啊...连边 $i->(i+m)\bmod n$ 长为m的边另外我们从S->i连一条长为i的边,因为第i天女生才能让他快乐

这样所有点最短路最大值就是答案啦,可是这个是1e9个点的,不可能过

考虑节省点数,压缩没有用的答案,因为初始快乐并不多所以我们考虑i和 $(i+m)\bmod n$ 二者如果都不快乐,那么i一定会在 $(i+m)\bmod n$ 前快乐,所以他的答案就没有用处了,我们把连向i的边连向 $(i+m)\bmod n$ 即可

这个思路是可以归纳到只保留i或(i+m) mod n为快乐节点的节点这个结论的,这样点数就只有b+g级别了

然后难点在于连边....我们考虑分几类边

源点到初始快乐节点
被保留的第二类节点到初始快乐节点边长为m
从初始快乐节点到被保留某个节点,边长xm

要求出第三类边长...我们考虑求那个被保留节点+m modn后的初始快乐节点是谁,那其实就相当于求modn意义下,每次向前跳m步,这样的一个初始快乐i遇到第一个初始快乐j是什么.....

直接做是n^2的,但是这个让人感觉有单调性,所以我们只需要把编号最小的那个点拿出来,对其他节点做一遍exgcd求出那个x,然后把那些节点按照x值排序,就可以得到快乐点i经过顺序,也就是要求的了

总复杂度O((b+g)log(b+g))?

code:


#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<map>
#include<vector>
#define ui unsigned int
using namespace std;
#define pi pair<int,int>
#define mp(x,y) make_pair(x,y)
#define ll long long
#define se second
#define fi first
//#define swap(x,y) (x^=y^=x^=y)

const int MAXN = 1e5 + 7;
const ll inf = 0x3f3f3f3f3f3f3f;
int n, m, d, B, G, b[MAXN], g[MAXN];
vector<int> a[MAXN << 1], f[MAXN << 1];
ll ans;

int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a;
}

int exgcd(int a, int b, int &x, int &y, int d = 0) {
    return b ? (d = exgcd(b, a % b, y, x), y -= a / b * x, d) : (x = 1, y = 0, a);
}



namespace fastIO {
#define BUF_SIZE (1<<19)
    static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = buf + BUF_SIZE;
    inline char nc() {
        if(p1 == pend) {
            p1 = buf;
            pend = buf + fread(buf, 1, BUF_SIZE, stdin);
        }
        return *p1++;
    }

    inline int read() {
        int x = 0, f = 1;
        register char s = nc();
        for(; !isdigit(s); s = nc())if(s == '-')f = -1;
        for(; isdigit(s); s = nc())x = (x << 1) + (x << 3) + s - '0';
        return x * f;
    }

}
using namespace fastIO;

inline ll solve(vector<int> a, vector<int> b) {
    vector<int> s = a;
    for(ui i = 0; i < b.size(); ++i)s.push_back(b[i]);
    sort(s.begin(), s.end());
    int k = unique(s.begin(), s.end()) - s.begin(), x, y;
    //去重之后
    if(n == k) {
        //puts("QWQ");
        int c[m];
        memset(c, 0, sizeof(c));
        for(ui i = 0; i < a.size(); ++i)if(a[i] < m)++c[a[i]];
        for(ui i = 0; i < b.size(); ++i)if(b[i] < m)++c[b[i]];
        for(int i = m - 1; ~i; --i)if(c[i] == 1)return i;
        return -1;
    }
    vector<pair<int, ll > > e[2 * k + 1];
    //printf("%d?%d\n", m, k);
    for(int i = 0; i < k; ++i)e[2 * k].push_back(mp(i, s[i])), e[i + k].push_back(mp(i, m));
    //S->s[i]
    exgcd(m, n, x, y);
    x = (x % n + n) % n;
    //printf("%d@\n", x);
    pi p[k];
    for(int i = 0; i < k; ++i)p[i] = mp(1ll * x * (s[i] - s[0]) % n, i); //printf("%d*%d\n", p[i].fi, p[i].se);
    sort(p, p + k);
    for(int i = 0, j = 1 % k; i < k; ++i, j = (++j == k) ? 0 : j)e[p[i].se].push_back(mp(p[j].se + k, 1ll * m * (p[j].fi - p[i].fi - 1 < 0 ? p[j].fi - p[i].fi - 1 + n : p[j].fi - p[i].fi - 1)));
    map<int, int> h;
    for(int i = 0; i < k; ++i)h[s[i]] = i;
    for(int i = 0; i < k; ++i) {
        if(h.find((s[i] + m) % n) != h.end()) {
            int j = h[(s[i] + m) % n];
            e[i].push_back(mp(j + k, 0)), e[j + k].push_back(mp(i, 0));
        }
    }
    priority_queue<pair<ll, int> > q;
    int v[2 * k + 1];
    ll d[2 * k + 1], now = 0;
    memset(v, 0, sizeof(v));
    memset(d, 0x3f, sizeof(d));
    q.push(mp(0, 2 * k)), d[2 * k] = 0;
    while(!q.empty()) {
        int x = q.top().se;
        q.pop();
        //printf("%d?\n", x);
        if(v[x])continue;
        v[x] = 1;
        now = max(now, d[x]);
        //所有最短路最长的
        for(ui i = 0; i < e[x].size(); ++i) {
            int v = e[x][i].fi;
            ll z = e[x][i].se;
            if((d[v] > d[x] + z))d[v] = d[x] + z, q.push(mp(-d[v], v));
        }
    }
    return now;
}

int main() {
   // freopen("test.in", "r", stdin);
    n = read();
    m = read();
    B = read();
    for(int i = 1; i <= B; ++i)b[i] = read();
    G = read();
    for(int i = 1; i <= G; ++i)g[i] = read();
    if(n < m)swap(n, m), swap(B, G), swap(b, g);
    if((d = gcd(n, m)) > (B + G))return puts("-1"), 0;
    n /= d; m /= d;
    //printf("%d!\n", d);
    for(int i = 1; i <= B; ++i)a[b[i] % d].push_back(b[i] / d);
    for(int i = 1; i <= G; ++i)f[g[i] % d].push_back(g[i] / d);
    for(int i = 0; i < d; ++i)
        if(!a[i].size() && !f[i].size())
            return puts("-1"), 0;//一组都没有开心
    for(int i = 0; i < d; ++i)ans = max(ans, solve(a[i], f[i]) * d + i);//再乘d才是一轮
    printf("%lld\n", ans);
    return 0;
}

夏晓光(loveJY)的博客

P5311 [Ynoi2011]成都七中