CF521E Cycling City

IOI2020集训队作业

已经预感不能再像现在这样刷题了...唉,准备开学吧

给定一张 $n$ 个点 $m$ 条边的无向简单图。
问图中能否找到两个点，满足这两个点之间有至少三条完全不相交的简单路径。
$n,m \le 2 \times 10^5$ ，图不保证连通。

这个题真的是构造题啊....因为我们只需要构造出一种通用的情境满足题意就行了QAQ,所以图论好像大部分这样裸的都是构造啊

怎么构造呢?先观察样例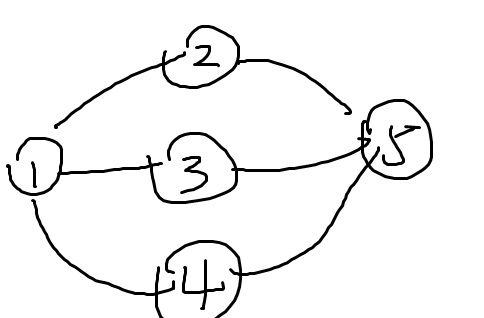

不难发现一个合法的一对点一定是两个环重复的部分

这个显然充分,必要性....因为是无向图好像是一样的吧QAQ....

所以问题变成了找有没有这样被两环覆盖的,经典问题

考虑先建出dfs树,然后对于一条非树边暴力覆盖到另一端点上所有点,然后直到某一刻有一个点被覆盖了2次,说明他是两环重复了

我们覆盖时也并不直接记次数,而是记哪条非树边覆盖他

不妨令 dfs 树作为生成树，令 b 为 a 的祖先，d 为 c 的祖先，b 的深度比 d 的深度浅。

不需要任何分类讨论，画个图就很容易明白，三条路径铁定就是：

d -> lca(a, c)
d -> b -> a -> lca(a, c)
d -> c -> lca(a, c)

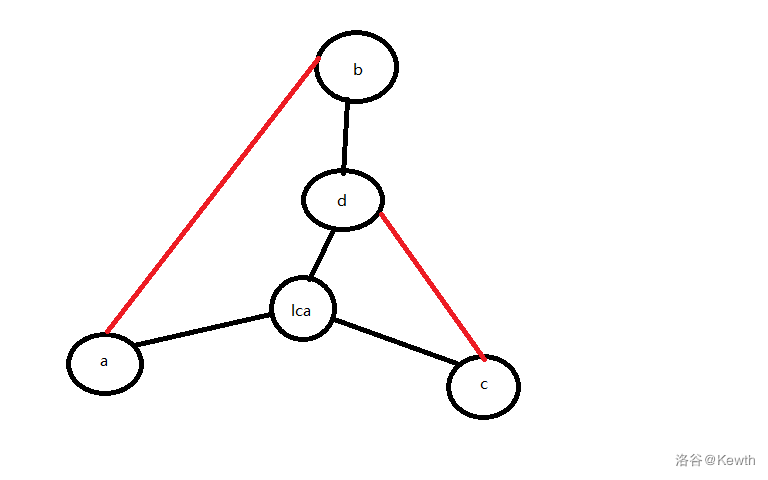
这样就好了所以我们还差个复杂度分析/jk

你会惊人的发现每个点最多被这样暴力跳过一次,因为如果暴力跳过两次就相当于找到答案了

所以复杂度是线性的

code:


#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#define ll long long
#define CT const int&
using std::reverse;
const int MAXN = 6e5 + 7;
int n, m, ccnt;
int home[MAXN], nxt[MAXN], to[MAXN];
bool vis[MAXN], ins[MAXN];
int fa[MAXN], deep[MAXN];
int cx[MAXN], cy[MAXN];

int LCA(int x, int y) {
	while(deep[x] > deep[y])x = fa[x];
	while(deep[y] > deep[x])y = fa[y];
	while(x != y)x = fa[x], y = fa[y];
	return x;
}

int tmp[MAXN], tp;

inline void ct(CT x, CT y) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
}

void addpath(int x, int y) {
	while(x != y) {
		tmp[++tp] = x;
		x = fa[x];
	}
	tmp[++tp] = y;
}
void print() {
	printf("%d ", tp);
	for(int i = 1; i <= tp; ++i) {
		printf("%d ", tmp[i]);
	}
	puts("");
	tp = 0;
}

#define swap(x,y) (x^=y^=x^=y)
inline void get(int a, int b, int c, int d) {
	if(deep[b] > deep[d]) {
		swap(a, c);
		swap(b, d);
	}
	int e = LCA(a, c);
	puts("YES");

    //就是对应了上图画的三种情况啊
	addpath(e, d);
	reverse(tmp + 1, tmp + tp + 1);
	print();

	addpath(d, b);
	addpath(a, e);
	print();

	tmp[++tp] = d;
	addpath(c, e);
	print();

	exit(0);
}

inline void dfs(int u) {
	deep[u] = deep[fa[u]] + 1;
	vis[u] = ins[u] = 1;
	//printf("%d?\n", u);
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v != fa[u]) {
			if(!vis[v]) {
				fa[v] = u;
				dfs(v);
			} else if(ins[v]) {
				for(int x = u; x != v; x = fa[x]) {//这一步线性
					if(cx[x] && cy[x]) {
						get(cx[x], cy[x], u, v);//这两个路径交点
					} else {
						cx[x] = u;
						cy[x] = v;//标记一整个路径
					}
				}
			}
		}
	}
	ins[u] = 0;
}

int main() {
	scanf("%d%d", &n, &m);
	for(int i = 1, u, v; i <= m; ++i) {
		scanf("%d%d", &u, &v);
		ct(u, v);
		ct(v, u);
	}
	for(int i = 1; i <= n; ++i)if(!vis[i])dfs(i);
	puts("NO");
	return 0;
}

夏晓光(loveJY)的博客

CF555E Case of Computer Network