CF526G Spiders Evil Plan

IOI2020集训队作业

最近莫名其妙的繁忙,是文化课更用功了吗?因为感觉不像颓了啊....

给定一棵 $n$ 个节点的无根树，每条边有边权。
有 $q$ 次询问，每次询问给出 $x,y$ ，你需要选择 $y$ 条树上的路径，使这些路径形成一个包含 $x$ 的连通块，且连通块中包含的边权和最大。
$n, q \le 10^5$ ，强制在线。

well,我承认一开始看成选边了,然后一点也没做出来,想了一个很假的n^2(

既然要选就选一条路径,那么我们可以考虑拿出一个结论

任意一个有k个叶子的树我们只需要k/2上取整条路径就能全覆盖

有了这个结论我们贪心就好贪了,问题变成在原树中选取一些叶子,使他们组成的极小连通块边权和最大

我们会发现直径的某一端点一定会被选,但是直径不定被选上...比如只有一条路径的情况

然后我们就可以分别以这两个直径端点为根建树,然后问题就是在其中子树选2k-1个叶子,最大化打通他们到根的边权和...~~还是不会做~~

考虑带边权的长链剖分啊所以我们只需要选前2y-1个最长链就好啦!!!实现的时候我们可以先把链头都存到数组里排序一下....

不过显然选完之后不一定经过x,需要微调

case 1

先选前2k-2条长链,然后第k条选择从x上方一个在前2k-2条长链中的点到x子树的叶子最大的

就是: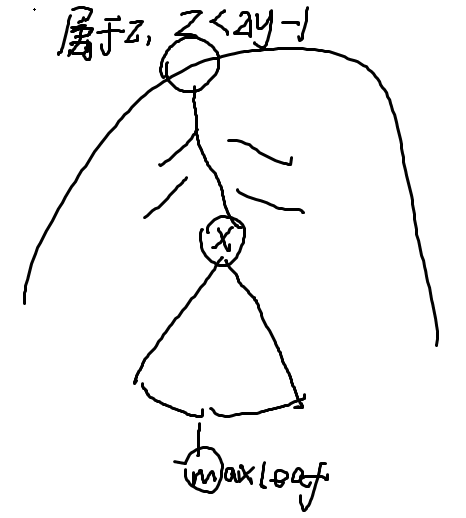

##case 2

选择前2k-1条长链,然后x去更换某条长链

就是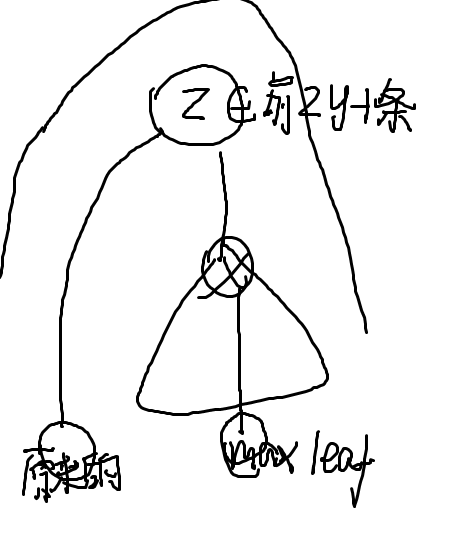

code:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define pi pair<int,int>
using std::max;
using std::sort;
const int MAXN = 4e5 + 7;
int n, q, k, s, ans, ccnt;
int home[MAXN], nxt[MAXN], to[MAXN], len[MAXN];


inline void ct(int x, int y, int z) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
	len[ccnt] = z;
}

namespace fastIO {
#define BUF_SIZE (1<<19)
	static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = BUF_SIZE + buf;
	inline char nc() {
		if(p1 == pend) {
			p1 = buf;
			pend = buf + fread(buf, 1, BUF_SIZE, stdin);
		}
		return *p1++;
	}
	inline int read() {
		int x = 0, f = 1;
		register char s = nc();
		for(; !isdigit(s); s = nc())if(s == '-')f = -1;
		for(; isdigit(s); s = nc())x = (x << 1) + (x << 3) + s - '0';
		return x * f;
	}

}
using namespace fastIO;
const int MAXM = 2e5 + 7;
struct rec {
	int root, f[MAXM][21], g[MAXM][21], d[MAXN], dep[MAXN], son[MAXN], top[MAXN], rnk[MAXN];
	int l[MAXN], r[MAXN], s[MAXN], t;

	void dfs1(int u, int F) {
		//printf("%d %d\n",u,F);
		for(int i = home[u]; i; i = nxt[i]) {
			int v = to[i];
			if(v != F) {
				d[v] = d[u] + len[i],
					   dfs1(v, u);
                       //得到dis值
			}
		}
	}

	void dfs2(int u) {
		for(int i = home[u]; i; i = nxt[i]) {
			int v = to[i];
			if(v != f[u][0]) {
				f[v][0] = u;
				g[v][0] = len[i];
				for(int j = 0; f[v][j]; ++j) {
					f[v][j + 1] = f[f[v][j]][j];
					g[v][j + 1] = g[v][j] + g[f[v][j]][j];
				}
				d[v] = d[u] + len[i];
				dfs2(v);
				if(dep[v] + len[i] > dep[u])
					dep[u] = dep[v] + len[i], son[u] = v;
                    //深度最大的
			}
		}//长链剖分??
		for(int i = home[u]; i; i = nxt[i]) {
			int v = to[i];
			if(v != f[u][0] && v != son[u])
				s[l[++t] = v] = dep[v] + len[i];
                //其他边向上到链头的距离
			    //其实就是把链头拿出来了
		}
	}

	void getroot(int u) {
		dfs1(u, 0);
		root = u;
		for(int i = 1; i <= n; ++i)if(d[i] > d[root])root = i;
		//直径一端点
		d[root] = 0;
		dfs2(root);
		s[l[++t] = root] = dep[root];
		sort(l + 1, l + t + 1, [&](int i, int j) {
			return s[i] > s[j];
		});
		//按照dep从大到小
		for(int i = 1; i <= t; ++i)r[i] = r[i - 1] + s[l[i]];
		for(int i = 1; i <= t; ++i) {
			int x = l[i], p = x;
			while(x) {
				top[x] = p;
				rnk[x] = i;//第几条长链,这里是按照长度排过序的
				//处理top
				x = son[x];
			}
		}
		//for(int i=1; i<=n; ++i) {
		//	printf("%d %d %d %d %d %d %d %d\n",s[i],top[i],rnk[i],son[i],dep[i],d[i],f[i][0],g[i][1]);
		///}
	}

	inline int plan1(int x, int y) {
		int z = dep[x];
		for(int i = 20; ~i; --i) {
			if(rnk[f[x][i]] >= y)z += g[x][i], x = f[x][i];
		}
		return r[y - 1] + z + g[x][0];
		//先用z-1条链
		//再用一条从x的叶子->z最长的打通x
	}

	inline int plan2(int x, int y) {
		int z = dep[x];
		for(int i = 20; ~i; --i) {
			if(rnk[f[x][i]] > y)z += g[x][i], x = f[x][i];
		}
		return r[y] - dep[f[x][0]] + z + g[x][0];
		//选前y条,然后扣去第y条后半部分接上x
	}
	inline int ask(int x, int y) {
		y = 2 * y - 1;
		return rnk[x] <= y ? r[y] : max(plan1(x, y), plan2(x, y));
	}

} t[2];
int in[MAXN];
int main() {
	///freopen("test.in","r",stdin);
	n = read();
	q = read();
	for(int i = 1, x, y, z; i < n; ++i) {
		x = read(), y = read(), z = read();
		ct(x, y, z);
		ct(y, x, z);
		in[x]++;
		in[y]++;
		s += z;
	}
	for(int i = 1; i <= n; ++i)k += (in[i] == 1);
	//	printf("%d?\n", k);
	t[0].getroot(1), t[1].getroot(t[0].root);

	for(int i = 1, x, y; i <= q; ++i) {
		x = read(), y = read();
		x = (x + ans - 1) % n + 1;
		y = (y + ans - 1) % n + 1;
		ans = (2 * y >= k ? s : max(t[0].ask(x, y), t[1].ask(x, y)));
		printf("%d\n", ans);
	}
	return 0;
}

夏晓光(loveJY)的博客

case 1

CF521E Cycling City