CF575I Robots protection

IOI2020集训队作业

一日不更博,一日不睡觉

~~话说已经堕落到这种程度了吗~~

你需要在平面直角坐标系上进行 $q$ 次操作。
每次操作有两种，要么放置一个两条直角边平行于坐标轴的等腰直角三角形，要么查询某一个点被多少个三角形覆盖。
每个等腰直角三角形可以用四个参数 $dir,x,y,len$ 确定，其中 $dir \in [1,4]$ 表示三角形的方向， $(x,y)$ 表示直角的顶点坐标， $len$ 表示直角边的长度。
保证所有点的坐标都是整数且 $\in [1,n]$ 。
$n \le 5 \times 10^3$ , $q \le 10^5$

看上去是做不了的,直接暴力有0分的好成绩,所以我们考虑翻题解

又是二维树状数组/jk/jk/jk?

然后这里你会发现我们要维护斜坐标系的一个标记加减,也就是说我们单纯的一个直角区域内的加减不满足了

所以我们要用斜二测画法,满足y坐标变成原来的1/2

这样我们能满足这样的角的标记

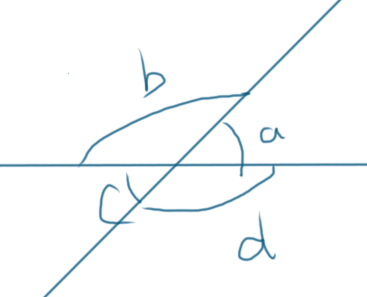
然后这样还是不太够,我们再把x变成原来的1/2,我们又可以满足

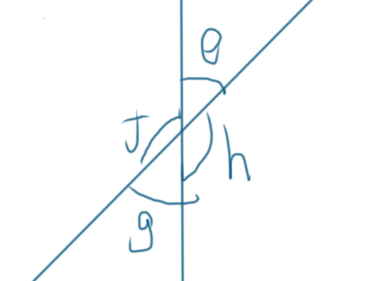
又因为显然等腰直角三角形满足的性质就只会设计这几个角啊

然后我们有罪恶的下图,按照下图去打标记统计前缀和就好了

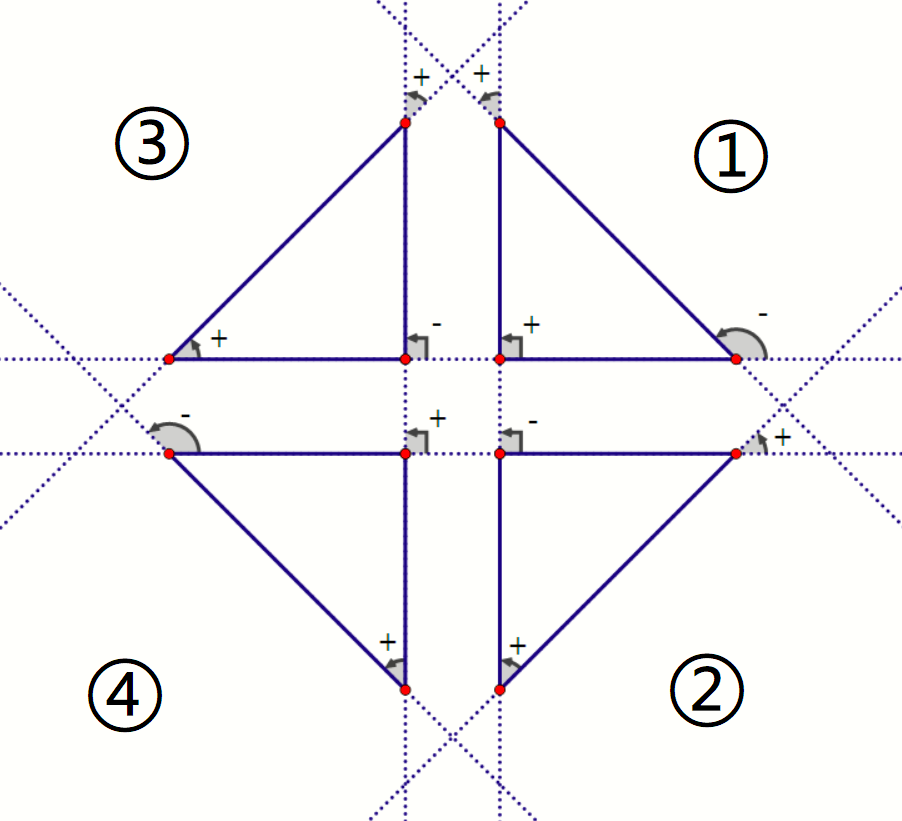
code:

#include<bits/stdc++.h>
#define lowbit(x) (x&(-x))
using namespace std;
const int MAXN = 1e4 + 7, MAXM = 1e5 + 7;
int n, m, op[MAXM], dir[MAXM], x[MAXM], y[MAXM], c[MAXM], ans[MAXM];
int X, Y, bit[MAXN][MAXN], stx[MAXM], sty[MAXM], stz[MAXM], top;

inline void add(int x, int y, int z) {
	stx[++top] = x;
	sty[top] = y;
	stz[top] = z;
	for(int i = x; i <= X; i += lowbit(i)) {
		for(int j = y; j <= Y; j += lowbit(j)) {
			bit[i][j] += z;
		}
	}
}

inline int ask(int x, int y) {
	int z = 0;
	for(int i = x; i; i -= lowbit(i)) {
		for(int j = y; j; j -= lowbit(j)) {
			z += bit[i][j];
		}
	}
	return z;
}

inline void clear() {
	while(top) {
		add(stx[top], sty[top], -stz[top]);
		top -= 2;
	}
}

int main() {
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= m; ++i) {
		scanf("%d", &op[i]);
		if(op[i] == 1)
			scanf("%d%d%d%d", &dir[i], &x[i], &y[i], &c[i]);
		else {
			scanf("%d%d", &x[i], &y[i]);
		}
	}
	
	X = n;
	Y = n;
	for(int i = 1; i <= m; ++i) {
		if(op[i] == 1) {
			if(dir[i] == 1)add(x[i], y[i], 1);
			if(dir[i] == 2)add(x[i], y[i] + 1, -1);
			if(dir[i] == 3)add(x[i] + 1, y[i], -1);
			if(dir[i] == 4)add(x[i] + 1, y[i] + 1, 1);
		} else {
			ans[i] += ask(x[i], y[i]);
		}
	}
	clear();

	X = n + n;
	Y = n;
	for(int i = 1; i <= m; ++i) {
		if(op[i] == 1) {
			if(dir[i] == 1)
				add(x[i] + y[i] + c[i] + 1, y[i], -1);
			if(dir[i] == 4)
				add(x[i] + y[i] - c[i], y[i] + 1, -1);
		} else {
			ans[i] += ask(x[i] + y[i], y[i]);
		}
	}
	clear();

	X = n;
	Y = n + n;
	for(int i = 1; i <= m; ++i) {
		if(op[i] == 1) {
			if(dir[i] == 1)
				add(n - x[i] + 2, x[i] + y[i] + c[i] + 1, 1);
			if(dir[i] == 4)
				add(n - x[i] + 1, x[i] + y[i] - c[i], 1);
		} else {
			ans[i] += ask(n - x[i] + 1, x[i] + y[i]);
		}
	}
	clear();

	X = n + n;
	Y = n;
	for(int i = 1; i <= m; ++i) {
		if(op[i] == 1) {
			if(dir[i] == 2)
				add(n + x[i] - y[i] + c[i] + 2, y[i] + 1, 1);
			if(dir[i] == 3)
				add(n + x[i] - y[i] - c[i] + 1, y[i], 1);
		} else {
			ans[i] += ask(n + x[i] - y[i] + 1, y[i]);
		}
	}
	clear();

	X = n;
	Y = n + n;
	for(int i = 1; i <= m; ++i) {
		if(op[i] == 1) {
			if(dir[i] == 2)
				add(x[i], n - x[i] + y[i] - c[i] + 1, 1);
			if(dir[i] == 3)
				add(x[i] + 1, n - x[i] + y[i] + c[i] + 2, 1);
		} else {
			ans[i] += ask(x[i], n - x[i] + y[i] + 1);
		}
	}
	clear();
	for(int i = 1; i <= m; ++i)
		if(op[i] == 2)printf("%d\n", ans[i]);

	return 0;
}

夏晓光(loveJY)的博客

CF576D Flights for Regular Customers