夏晓光(loveJY)的博客

仍要向下扎根,向上结果

首页 归档 标签 关于 友链

CF613E Puzzle Lover

2020-07-21 13 min read # 字符串 # 字符串hash # 动态规划

IOI2020国家集训队作业

重 操 旧 业 估计应该能做完part1,part2,part3都是AT题不太行啊

  • 给定一个 2×n2 \times n 的矩阵，每个位置上有一个小写字母。
  • 有一个长度为 kk 的小写字符串 ww，询问矩阵中有多少条有向路径满足以下条件：
    • 路径上的字母连起来恰好为 ww。
    • 不多次经过同一个位置。
    • 只能向上下左右四个方向走。
  • n,k≤2×103n,k \le 2 \times 10^3，答案对 109+710^9+7 取模。

首先想少的我想DP,dp[i][j][k][l]表示前i列第j行,然后匹配了k个位置,前一个转折点在l的最多方案数是什么

显然是没法转移的,因为我们成环,而且可能像蛇一样弯曲前行...

但是转念一想这个环是不是太过basic了?好像不会复杂

就是说一个回头路一定是在字符串的开头或者结尾才有可能?

就例如下图,这是最复杂的路径情况了

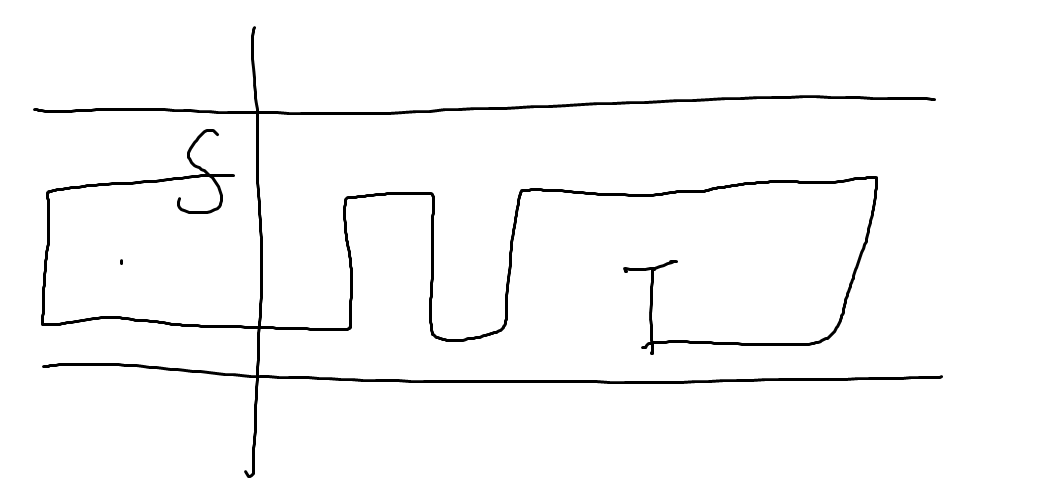
然后我们可以想办法搞定这个...中间部分?

你发现中间部分是蜿蜒曲折的,两边的回头路是简单的

所以我们可以只考虑中间设计dp,f[i][j][k]表示点i,j匹配了k的方案数并且下一步只能走同一行的点,g[i][j]表示点i,j匹配了k的方案数并且下一步只能走同一列的点转移

然后怎么算呢?

fi,j,k=∑fi,j−1,k−1[chi,j==tk]f_{i,j,k}=\sum{f_{i,j-1,k-1}[ch_{i,j}==t_k]}

g3−i,j,k=∑fi,j,k−1[ch3−i,j==tk]g_{3-i,j,k}=\sum{f_{i,j,k-1}[ch_{3-i,j}==t_k]}

fi,j,k=∑gi,j−1,k−1[chi,j==tk]f_{i,j,k}=\sum{g_{i,j-1,k-1}[ch_{i,j}==t_k]}

转移的时候推荐从现在向后转移,因为有一些不合法状态

第三个转移的意思是我们考虑转一个弯之后又向前走了一步,当然也是可以的qwq,3-i是第一二行之间切换

然后两边部分QAQ,你发现我们决定哪个为起点会影响中间这个DP过程啊

不过您又机智的发现这个是一个可以预处理然后特判能不能相等的部分,也就是说我们可以搞搞DP数组的初值来解决他?

具体的,对于如果从S走长度为大于1的x的回头路,我们可以看这个回头路能不能匹配串的前2x个字符,如果能,说明从S另一列的位置处g3−i,j,2xg_{3-i,j,2x}可以置为1

若长为等于1,说明就是从S向下走了一步,gi,j,2g_{i,j,2}可以置为1

同时,如果这个点本身就是能匹配的,说明gi,j,1g_{i,j,1}可置为1

为什么只用g数组初始化?因为f数组可以和g相互update,同时我们统计答案也是看g数组的

然后我们再考虑T的部分,也就是统计答案这部分QAQ

首先我们第三维小于m,给T一点面子

然后如果T处一个长为x的后缀回头路可以匹配后2x个字符的话,我们就把fi,j−1,m−2x+gi,j−1,m−2xf_{i,j-1,m-2x}+g_{i,j-1,m-2x}统计入答案,相当于我们手动走这最后一步

然后我们发现我们没有处理从右往左走的情况,所以可以把串翻转之后再跑一遍上述过程....

然后您惊人的发现我们算重了,但是只算重了S和T在同一列的情况,所以这个很好用hash处理,就可以放在外面再加上!

然后我们就完成了一道国家集训队作业题....QAQ

然后写的时候有很多很多细节.....

  1. 单模hash也能过,双模hash不可写
  2. 子串merge的规则:

s同一行的得到(从左向右)ap3+bp2+cp+dap^3+bp^2+cp+d

t同一行的得到**a′+b′p1+c′p2+d′p3a'+b'p^1+c'p^2+d'p^3**

然后t整体乘上p4p^4,即长度的一半

  1. m=1的时候,整个dp是没有意义的,所以我们要直接特判匹配
  2. m=2的时候,我们后面统计t的时候会和计算s的时候又算重一次,所以后面那次直接不统计即可

code:(一下午/ll)


#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int P = 1e9 + 7;
const int B = 131;
const int MAXN = 3e3 + 7;
int n, m;
char s[3][MAXN], t[MAXN];
ll pre[3][MAXN], suf[3][MAXN], pret[MAXN], bas[MAXN];
inline void init() {
	bas[0] = 1;
	for(int i = 1; i <= max(n, m); ++i) {
		bas[i] = 1ll * bas[i - 1] * B % P;
	}
	for(int i = 1; i <= n; ++i) {
		pre[1][i] = (pre[1][i - 1] * B + s[1][i] - 'a' + 1) % P;
		pre[2][i] = (pre[2][i - 1] * B + s[2][i] - 'a' + 1) % P;
	}
	for(int i = n; i >= 1; --i) {
		suf[1][i] = (suf[1][i + 1] * B + s[1][i] - 'a' + 1) % P;
		suf[2][i] = (suf[2][i + 1] * B + s[2][i] - 'a' + 1) % P;
	}
	return;
}

ll ans1, ans;
int f[3][MAXN][MAXN], g[3][MAXN][MAXN];

inline ll getpre(int x, int y, int id) {
	return (pre[id][y] - pre[id][x - 1] * bas[(y - x + 1)] % P + P) % P;
}


inline ll getsuf(int x, int y, int id) {
	return (suf[id][x] - suf[id][y + 1] * bas[(y - x + 1)] % P + P) % P;
}

inline ll merge(ll x, ll y, ll L) {
	return (y + 1ll * x * bas[L] % P) % P; //先走的计算的多
}


inline void solve() {
	memset(g, 0, sizeof(g));
	memset(f, 0, sizeof(f));
	pret[0] = 0;
	for(int i = 1; i <= m; ++i) {
		pret[i] = (pret[i - 1] * B % P + t[i] - 'a' + 1) % P;
	}
	for(int k = 1; k <= 2; ++k)
		for(int i = 1; i <= n; ++i) {
			for(int j = 1; j <= i; ++j) {
				int len = (i - j + 1) * 2;
				if(len > m)continue;
				ll S1 = getpre(j, i, k);
				ll S2 = getsuf(j, i, 3 - k);
				ll T1 = pret[len];
				// printf("%d %d %d %d %lld %lld %lld???\n", k, i, j, len, S1, S2, T1);
				if(merge(S2, S1, i - j + 1) == T1) {
					// printf("qwq?%d %d \n", i, j);
					if(len == m) {
						ans1++;
					} else g[k][i][len] = 1;
				}
			}
		}
	for(int k = 1; k <= 2; ++k)
		for(int i = 1; i <= n; ++i) {
			if(t[1] == s[k][i])
				g[k][i][1] = 1;
		}
	// for(int k = 1; k <= 2; ++k)
	// 	for(int i = 1; i <= n; ++i) {
	// 		for(int j = 1; j <= m; ++j) {
	// 			printf("%d  ", g[k][i][j]);
	// 		}
	// 		puts("");

	// 	}
	for(int j = 1; j < m; ++j) {
		for(int i = 1; i <= n; ++i) {
			for(int k = 1; k <= 2; ++k) {
				if(g[k][i][j]) {//已有
					if(i < n && s[k][i + 1] == t[j + 1]) {
						f[k][i + 1][j + 1] = (1ll * f[k][i + 1][j + 1] + g[k][i][j]) % P;
					}
				}
				if(f[k][i][j]) {//可有
					if(i < n && s[k][i + 1] == t[j + 1]) {
						f[k][i + 1][j + 1] = (1ll * f[k][i + 1][j + 1] + f[k][i][j]) % P;
					}
					if(s[3 - k][i] == t[j + 1]) {
						g[3 - k][i][j + 1] = (1ll * g[3 - k][i][j + 1] + f[k][i][j]) % P;
					}
				}
			}
		}
	}
	for(int i = m; i >= 1; --i) {
		pret[i] = (pret[i + 1] * B % P + t[i] - 'a' + 1) % P;
	}
	for(int k = 1; k <= 2; ++k) {
		for(int i = 1; i <= n; ++i) {
			if(s[k][i] == t[m]) {
				if(m == 1)ans++;
				ans = (ans + f[k][i - 1][m - 1]) % P;
				ans = (ans + g[k][i - 1][m - 1]) % P;
				// printf("%lld?\n", ans);
				ans %= P;
			}
			for(int j = i; j <= n; ++j) {
				int len = (j - i + 1) * 2;
				if(len > m)continue;
				ll S1 = getpre(i, j, 3 - k);
				ll S2 = getsuf(i, j, k);
				ll T2 = pret[m - len + 1];
				if(merge(S1, S2, j - i + 1) == T2) {
					// printf("%d %d %d %dqwq?\n", k, i, j, len);
					// puts("qwq");
					if(len == m && m != 2)
						ans1++;
					else {
						ans = (ans + f[k][i - 1][m - len]) % P;
						ans = (ans + g[k][i - 1][m - len]) % P;
						// printf("%lld?\n", ans);
						ans %= P;
					}
				}
			}
		}
	}
	return ;
}

int main() {
	// freopen("test.out", "w", stdout);
	cin >> (s[1] + 1);
	cin >> (s[2] + 1);
	cin >> (t + 1);
	n = strlen(s[1] + 1);
	m = strlen(t + 1);
	init();
	solve();
	reverse(t + 1, t + m + 1);
	solve();
	ans = (ans + ans1 / 2) % P;
	if(m == 1)ans /= 2;
	printf("%lld\n", ans);
	return 0;
}

另附赠一开始膨胀的我写的几十行双模运算类


struct HASH1 {
	ll V;
	HASH1(ll x = 0): V(x) {};
	inline HASH1 &operator *= (const ll &x) {
		V = V * x % P1;
		return  *this;
	}
	inline HASH1 &operator += (const int &x) {
		V = (V + x) % P1;
		return  *this;
	}
	inline HASH1 &operator -= (const ll &x) {
		V = V - x + P1;
		V %= P1;
		return  *this;
	}
	inline HASH1 operator + (const int &x) const {
		HASH1 qwq = *this;
		return HASH1((qwq.V + x) % P1);
	}

	inline HASH1 operator * (const ll &x)const {
		HASH1 qwq = *this;
		return HASH1(qwq.V * x % P1);
	}

	inline HASH1 operator - (const ll &x)const {
		HASH1 qwq = *this;
		return HASH1((qwq.V - x + P1) % P1) ;
	}
};
struct HASH2 {
	ll V;
	HASH2(ll x = 0): V(x) {};
	inline HASH2 &operator += (const int &x) {
		V = (V + x) % P2;
		return  *this;
	}
	inline HASH2 &operator *= (const ll &x) {
		V = V * x % P2;
		return  *this;
	}
	inline HASH2 &operator -= (const ll &x) {
		V = V - x + P2;
		V %= P2;
		return  *this;
	}
	inline HASH2 operator + (const int &x)const {
		HASH2 qwq = *this;
		return HASH2((qwq.V + x) % P2);
	}
	inline HASH2 operator * (const ll &x)const {
		HASH2 qwq = *this;
		return HASH2(qwq.V * x % P2);
	}
	inline HASH2 operator - (const ll &x)const {
		HASH2 qwq = *this;
		return HASH2((qwq.V - x + P2) % P2);
	}
};
struct HASH {
	HASH1 V1;
	HASH2 V2;
	HASH() {};
	HASH(HASH1 V1, HASH2 V2): V1(V1), V2(V2) {};
	inline HASH operator + (const int &x) {
		HASH qwq = *this;
		qwq.V1 += x;
		qwq.V2 += x;
		return qwq;
	}
	inline HASH operator + (const HASH &x) {
		HASH qwq = *this;
		qwq.V1.V = (qwq.V1.V + x.V1.V) % P1;
		qwq.V2.V = (qwq.V2.V + x.V1.V) % P2;
		return qwq;
	}
	inline HASH operator - (const HASH &x) {
		HASH qwq = *this;
		qwq.V1.V -= x.V1.V;
		qwq.V2.V -= x.V2.V;
		qwq.V1.V += P1;
		qwq.V1.V %= P1;
		qwq.V2.V += P2;
		qwq.V2.V %= P2;
		return qwq;
	}
	inline HASH operator * (const int &x) {
		HASH qwq = *this;
		qwq.V1 *= B1[x];
		qwq.V2 *= B2[x];
		return qwq;
	}
	bool operator==(const HASH &x)const {
		return x.V1.V == V1.V && x.V2.V == V2.V;
	}
};
Powered by Gridea RSS