A. K-th Largest Value

No solution

B. Minimal Cost

注意到我们最多只有上下一列的阻隔,阻隔当且仅当满足任意两个数他们相差不超过1

答案初始化位2*v和u+v最小值,然后考虑如果不是一列的情况,我们一定能通过一个上下交换或者左右交换达到

我的做法很假啊

就是对于大于n的直接判掉他们一定没用

然后小于n的,我们考虑只用 $O(\sum a_i)$ 的复杂度消除他们

因此建立一个并查集,然后只把那些为1的连接到下一个位置,然后每次加速非1位置的跳跃,然后不是1的就暴力-1跳到下一个位置即可

观察发现操作不会使1的个数变多,每个数不能像小于他的数到达

因此我们比较大小为第一要义

然后从小到大扫描,如果哪一个瞬间v的1的数量比u的1的数量多了,说明不行

否则我们一定有一个方法调整1的数量和位置使得合法,因为v>u

复杂度 $O(q*30)$

一开始直接写了一个只判断第一层是否合法的dfs,然后他WA了

然后我把他变成每一层都递归下去判断是否合法,就是Fib_n合法分裂成的两个大小为 $F_{n-1},F_{n-2}$

再判断两个树是不是合法

这个竟然是对的,证明可以考虑如果我们有两个合法的边,那么我们选择第一条边砍掉,得到 $F_{n-1},F_{n-2}$

那么 $F_{n-1}$ 一定包含另一条合法边,然后再把那条边断掉得到 $F_{n-2}$ (另一侧),和 $F_{n-1}-F_{n-2}$ (同一侧)

也就是说无论我们把它拖到什么时候割开都是合法的!

先把前i-1个放入左边第i个放入右边,如果有磁力说明前i-1个有一个有磁力,然后第i个也有磁力

那么我们二分查找前i-1个得到那个有磁力的,剩下都是没有磁力的,然后再用第i个检测后面的即可

偶数个环怎么做?

用一次操作随意交换两个位置使得环变成两个环的并,此时有两个反面的硬币!

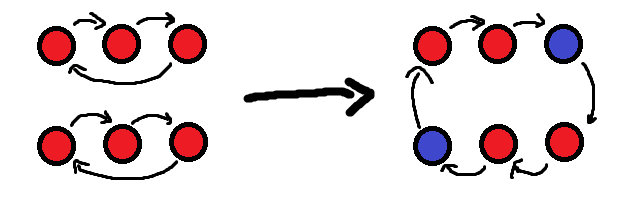
然后我们有用n-1次操作得到一个回复好的序列的过程,就是用反面的币向前推交换,知道前面是另一个蓝色的币,就再用那个币向前推交换,最后一次交换两个蓝色的币即可

操作次数X(等于环长)

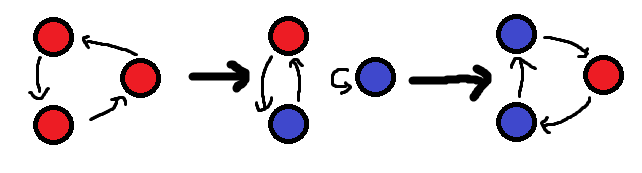
一个环怎么做?

如果有其他的一个点的自环,我们还可以拆开环,这样是 $O(X+1)$

否则整张图就是一个环,我们可以考虑两次操作强行拆出两个蓝点,然后再用上述过程

没看懂题解啊,lxl咋回事啊

就知道他要维护一个祖先满足父亲能够跳出x所在的块内,然后我也知道询问可以用树分块的方法做

但剩下不会了