A. Anti-knapsack

注意$k<n$

答案可以达到啥n-k+k/2的上界

就是大于k的数和$k/2到k$

B. Planet Lapituletti

镜像不会改变的只有0,1,2,5,8,其中2,5会互换

然后观察数据范围,我们想到儒略历一个牛逼的做法:打表

所以枚举每一分钟向上加判断即可

C

枚举哪一位开始大于即可,然后贪心的尽量填大于他最小的字符

考场上因为z这种字符自闭了!!

剩下一些整除k的限制看看代码即可

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e6 + 7;
int T, n, K, res;
char s[MAXN];
int pre[MAXN][27], a[MAXN], avi[MAXN];

inline int pd(int x) {//判断什么?
	//前面的能放下
	if(s[x] == 'z')return 0;//大于你妈个头
	res = 0;
	for(int i = 0; i < 26; ++i) {
		avi[i] = (K - (pre[x - 1][i] % K)) % K;
		res += avi[i];
	}
	if(n - x + 1 < res || (n - x + 1 - res) % K != 0)return 0; //如果不够,或者说剪掉之后还不太行就不能
	res = (n - x + 1 - res) / K;
	if(res <= 0) {
		for(int i = s[x] - 'a' + 1; i < 26; ++i)
			if(avi[i])
				return 1; //有一个牛逼的就行
		for(int i = 0; i < 26; ++i)avi[i] = 0;
		return 0;
	} else {
		if(!avi[s[x] - 'a' + 1]) {
			res--;
			avi[s[x] - 'a' + 1] += K;
		}
		return 1;//浪费一个
	}
}

inline void solve(int x) {//输出方案!
	for(int i = s[x] - 'a' + 1; i < 26; ++i)
		if(avi[i]) {
			a[x] = i;
			avi[i]--;
			break;
		}
	for(int i = n; i > x; --i) {//只构造后面的部分
		bool flg = 1;
		for(int k = 25; k >= 0; --k)
			if(avi[k]) {
				a[i] = k;
				avi[k]--;
				flg = 0;
				break;
			}
		if(flg)a[i] = 0;
	}
	for(int i = 1; i < x; ++i)a[i] = s[i] - 'a';
	for(int i = 1; i <= n; ++i)printf("%c", a[i] + 'a');
	puts("");
	return ;
}

int main() {
	scanf("%d", &T);
	while(T-- > 0) {
		scanf("%d%d", &n, &K);
		scanf("%s", s + 1);
		for(int i = 1; i <= n; ++i) {
			for(int k = 0; k < 26; ++k) {
				pre[i][k] = pre[i - 1][k];
			}
			pre[i][s[i] - 'a']++;
		}
		bool flg = 1;
		if(pd(n + 1)) {
			printf("%s\n", s + 1);
			continue;
		}
		for(int i = n; i >= 1; --i) {
			if(pd(i)) {//如果这一位开始大于他,能不能行
				solve(i);
				flg = 0;
				break;
			}
		}
		if(flg)puts("-1");
	}
	return 0;
}

D

所有数的gcd等于每个质因数取min

直接维护所有非零的即可复杂度$O(nlogn)$

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ins insert
#define pii pair<int,int>
#define mkp(x,y) (make_pair(x,y))
#define fi first
#define se second
const int MAXN = 4e5 + 7;
const int P = 1e9 + 7;

ll ans;
int n, q, a[MAXN], lst[MAXN];
multiset<int> st[MAXN];
set<pii> v[MAXN];
int tot, isp[MAXN], pri[MAXN], mix[MAXN];

inline ll ksm(ll x, ll y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

inline void init() {
	int N = 2e5;
	for(int i = 2; i <= N; ++i) {
		if(!isp[i]) {
			isp[i] = 1;
			pri[++tot] = i;
			mix[i] = i;
		}
		for(int j = 1; j <= tot && i * pri[j] <= N; ++j) {
			isp[i * pri[j]] = 1;
			mix[i * pri[j]] = pri[j];
			if(i % pri[j] == 0)break;
		}
	}
	for(int i = 1; i <= n; ++i) {
		int num = 0;
		int p = a[i];
		while(p > 1) {
			num = 0;
			while(mix[p] == mix[p / mix[p]]) {
				num++;
				p /= mix[p];
			}
			num++;
			st[mix[p]].ins(num);
			v[i].ins(mkp(mix[p], num)); //次数,是啥
			p /= mix[p];
		}
	}
	ans = 1;
	for(int i = 1; i <= N; ++i) {
		lst[i] = 1;
		if(st[i].size() == n) {
			lst[i] = ksm(i, (*st[i].begin()));
			ans = ans * lst[i] % P;
		}
	}
	return ;
}

inline void solve(int i, int y) {
	int p = y;
	while(p > 1) {
		int num = 0;
		while(mix[p] == mix[p / mix[p]]) {
			num++;
			p /= mix[p];
		}
		num++;
		auto q = (v[i].lower_bound(mkp(mix[p], 0)));
		if(q == v[i].end()) {
			v[i].ins(mkp(mix[p], num));
			st[mix[p]].ins(num);
		} else {
			auto g = *q;
			if(g.fi == mix[p]) {
				v[i].erase(g);
				st[g.fi].erase(st[g.fi].find(g.se));//删掉一个!!!
				v[i].ins(mkp(g.fi, g.se + num));
				st[g.fi].ins(g.se + num);
			} else {//没有,我们要新建
				v[i].ins(mkp(mix[p], num));
				st[mix[p]].ins(num);
			}
		}
		if(st[mix[p]].size() == n) {
			ans = 1ll * ans * ksm(lst[mix[p]], P - 2) % P;
			lst[mix[p]] = ksm(mix[p], (*st[mix[p]].begin()));
			ans = 1ll * ans * lst[mix[p]] % P;
		}
		p /= mix[p];
	}
	printf("%lld\n", ans);
	return ;
}

int main() {
	scanf("%d%d", &n, &q);
	for(int i = 1; i <= n; ++i)scanf("%d", &a[i]);
	init();
	for(int i = 1, x, y; i <= q; ++i) {
		scanf("%d%d", &x, &y);
		solve(x, y);
	}
	return 0;
}

E

结论:

如果l,r跨越2的次幂,答案是全1,方案是

1000000

和

0111111

否则r是偶数而且$l\leq r-2$,答案是r+1,否则是r

证明可以数学归纳

假设前r-2个成立,显然r+1的方法是选择r,r-1,r-2就一定可以

然后你会发现如果有更大的位能成为1,在最高位的1不消失的情况下,只有至少让r的最高位为0才能异或出来,因为显然需要选择偶数个数,然后这些数都会有最高位的1

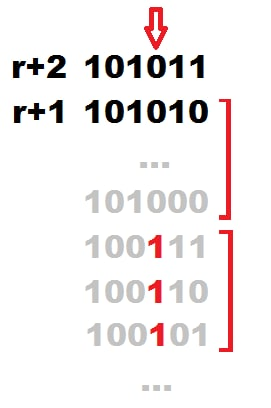
就做完了