CSP-S2考前综合强化讲课(Day 5)


菜啊
异或粽子的做法
前缀和
维护所有右端点当且最小左端点,然后我们每次找全局的右端点-左端点最大值
取出一个就把区间左右边的add进堆里
这样一直做下去直到找齐k个

显然这个东西在排序意义下就是取中位数
那么就是动态维护区间中位数

显然可以线段树二分,从最左侧到最右侧一次放广告,找到最左边第一个能放广告的位置,就把放进去剪掉空余
一直模拟到n即可

还是要维护一下的,前缀最大空房间位置,后缀最大空房间位置,然后一个区间总的最大空房间
然后线段树二分,能向左就向左
合并的时候两边最大和中间最大取max
然后修改直接把那些区间拿出来改改

堵塞的交通都是有毛病的题
维护一个区间左边一列连通性,右边一列连通性,区间连通块数
然后合并时候,我们考虑下左右连通新联通情况
同一连通块可以用一个编号存下
然后中间连通信息可以推出新的左右连通信息!
我们最多5个二进制位可以记录一个编号,那么20个数也可以用两个longlong存下,左边一个右边一个
合并的时候直接分配新标号
同时我们也可以计算出新减少的连通块数,因为但凡中间能够产生一次新的合并就要-1

偶数次???好像奇数次我们很会做
会发现我们是可以数据结构的
那么我们首先可以算出所有不同的数异或和
然后我们查出一个异或和之后异或上奇数的异或和即可

线段树维护那个EI/se
然后合并的时候也是异或一下
考虑每一位拿出来,然后新的式子是:
(^^+^+^+)(+ + + +)
显然第i位加起来的信息可以处理,每一位异或起来有多少1可以处理,每一位有多少一可以处理

默念口诀:
导函数值单增最大化单调栈
导函数值单减最大化单调队列
证明?
你考虑我们时间点只可能越来优,但是一开始可能还不到那个时间

一开始想三个数组每个元素找一个最小的出现位置,然后三个lst最小出现位置求和
这样假了
14567892
3333332
n^2显然可以枚举两个第三个单调变化
然后我们考虑枚举第一个,然后快速查询二三个数组的答案,
那么我们就能快速解决了
先考虑从后向前删除,因为加入限制显然比撤销限制更好做
把A数组每个值,钦点一个(x,y),x表示在第二个数组中最早出现的位置,y表示第三个数组最早出现的位置
然后我们要做的就是有最小的矩形把所有点都覆盖了
并不这样的,我们是要用最少的矩形把所有权值都覆盖了
但是由于我们每个点可能有相同的权值,所有很自闭
那么我们就仔细观察一下可能成为决策的那些点
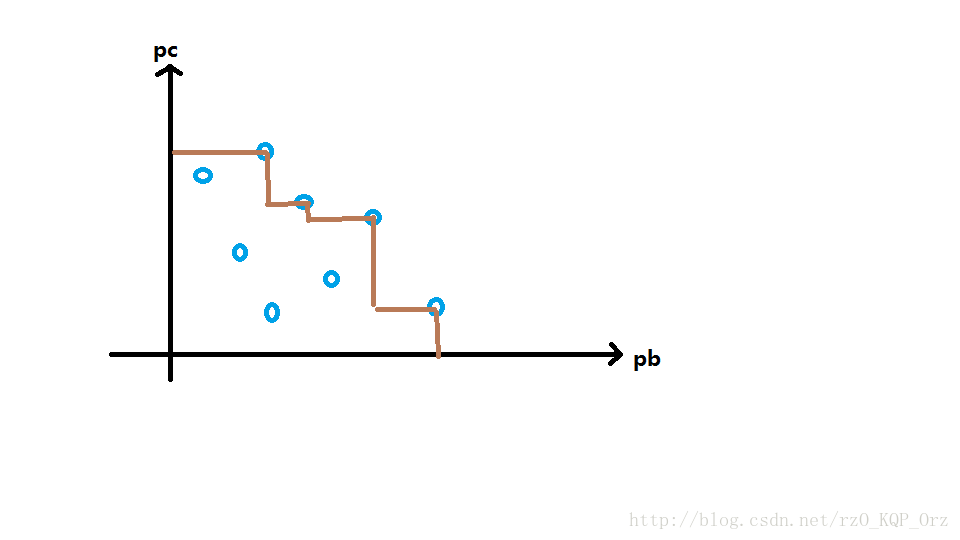
就是那些拐点!
为什么?
因为别忘了,我们的数组是小于等于,而现在点只是小于
选一个拐点就选了左及下方所有点
所以我们会发现这个拐点的右上方矩阵一定没有用了,因为不存在一个更早的元素
所以我们现在要维护的是:
- 一个类似于凸包的阶梯
- 所有拐点答案最大值
做法:
用set维护阶梯,即可,插入一个点会把那些都小于等于它的删掉,做法就是找到第一维大于他的然后向前跳,直到第二维不满足了
当然也要看第一个第一维大于他的
用heap维护答案也很显然,被删掉就lazypop,加入就push

显然这个题可以魔法森林
枚举一维,LCT一维

显然这个题可以根号平衡
O(1)修改,O(\sqrtn)查询
然后大小分块第一个

我的做法:
序列分块,时域分块
首先每个区间可以分块,记录答案
会发现修改后我们每个块暴力打标记即可
然后每个时域可以分块,当我们查到边角块的时候,暴力下放根号次修改即可
然后你会发现我们要每根号次重构,总复杂度就是什么O(n\sqrtm+m\sqrtn)
std:
上述做法愚蠢在于我们不能快速得到一些a的值
考虑我们把a分个块,然后你会发现修改一个a的值可以做到\sqrtn
然后查询一个a的值可以做到
然后函数我们也暴力分块就好了
做完了
小z的袜子
?
莫队的一个优化,奇偶分治
但是不要用了,飞哥亲口说的
就是左端点分块,相同右端点直接单增
优化就是左边的块是奇数的时候按照升序排序,否则按照降序排序


其实就是康拓展开的写法,考虑先停到哪个位置,然后我们再计算后面的贡献就好了