夏晓光(loveJY)的博客

奇数放左边,偶数放右边,然后递归下去

然后我们还可以发现,当全是偶数的时候我们会都除以2,全是奇数就没辙了

最大团可以搜索吗?

随机一个点然后暴力这样子

显然我们可以删掉度数小于$2n/3$的?

然后我们可以随便找到一堆没有边相连的点然后随便删掉一个然后剩下的点数$[n/3,n]$,一定会存在一个大于等于n/3的环

就算每次删团上的点也能存在啊

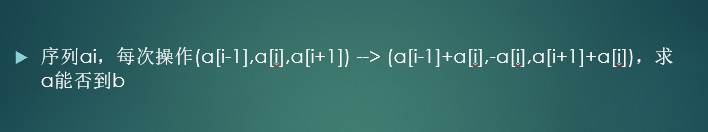
这个交换....

题解五个字:考虑前缀和

也就是说我们这个操作会交换两个相邻位置的前缀和

然后我们能换换换

所以只要前缀和数组排序后看上去一样就好

答案不会超过1e18?

不,不会超过1e5

因为$f_i<=f_{i/2}+2p+v$

这样log层

然后我们想能不能翻转值域和定义域呢?

然后我们可以写出关于p的式子

$f[i]=min(f[j]+(i+j-1)/j*p+v,ip+v)$

$g_i=max{i|f_i<=j}$

------|------k------

$k+\frac{i+g_k-1}{g_k}*p+v<=j$

只要满足这个条件就是可以的,可以用来更新$g_j$

枚举这个i就能n^2了!

发现本质上我们要被限制p,所以还能除个p?

画出树结构,发现转移树的层数$logn$

枚举这个层数,然后v的贡献是层数

然后尽量品均分,就是$p^d$(d
是深度)尽量接近i

$i+j-1/j$是每一层的最多的分叉

然后这每一层做完了.....

线段树太慢了

可以前缀积,然后进行矩阵求逆

行列式非0的$n*n$方阵是满秩的可以求逆

否则你求不了

矩阵求逆:

我们有如下线性变换:

1. 交换两行
2. 某一行加上另一行的某个数的某个倍数

那么我们就可以对于$A*B=I$

在高斯消元A到I的时候,对于B做同等线性变换即可

$O(n^3)$

2*2的矩阵可以手动解,就是这个题

AB xy
CD ->zw 1

然后这个可以解了

按照dfs的顺序???显然不行啊

max做法

你会发现最优构造每个都能卡到$min{siz,n-siz}^2$

至少走直径的方案是可以的

现在我们要让siz和n-siz尽量逼近

以重心为根,(n-siz>siz)然后每个子树下去按照深度最大的一次访问就好了

这样除了出发点不会有一条边能卡不住siz^2的下界qwq

min做法

我们有一条链可以最小化,只走一次,其他点都要走两次

那么就是直径了

然后构造的时候就是考虑直径的在回溯时候删,其他的之际加入即可qwq

大小分块

大的FFT,小的暴力

看看从下到上能不能把这个树缩成一个点

4合1

左下+一个点,右下+一个点,只有左儿子,右儿子

所以就是直接树哈希?不是,分配了编号后枚举一下每个点有没有就好了

怎么实现呢?

四类树,我们可以把森林中每一类符合条件都拿出来都向下递归一下,

即左边一个点,然后右边一颗树或者左边一棵树右边一个点

然后看能不能循环的把一个树上的点删掉直到没有点

qwq就听到这里啦,我们回家去了!