夏晓光(loveJY)的博客

枚举

for,或者while,或者do_while?/se

基本所有代码都要包括....

水仙花数

$O(n*log_{10}n)$

搜索

显然

坐等例题

NOI1999

n很小唉

可以考虑搜索出蛋糕最小表面积

用了多少总体积,到了第几层,半径和高

那么我们来剪枝!

可行性剪枝

1. 半径和高递减
2. 如果这一层用最优的方法去放都不能满足总体积就return

也就是半径1高度1->半径2高度2......

3. 如果这一层用最劣的方法都能放下就不搜

$R-1,H-1...R-2,H-2...$

说明我们之前的决策sb了

最优性剪枝

4. 当前表面积和+剩下的最小表面积都不能凑齐超过答案就return

你会发现当体积一定的时候剩下最小表面积应该能搞出来?

$V=\pi r^2 h$

$S=2\pi r h$

r最大为.....

然后能算出对应的h,就可以找到最小表面积了

相当于估价函数吧

显然可以暴力吧...$f_{lst,a[13]}$表示上一个是什么,然后面值为i的有多少张

不过状态有点多,会发现我们无论如何只看面值是否相同

$f_{lst,b[5]}$表示上一个是什么,然后重复i次的有多少面值

转移的时候选下一个是什么...?

枚举下最多多少个数k

搜搜当前最小的分母

你会发现如果我们最小分母的k倍小于剩下的数和就一定不可能可以剪一刀

就能跑出来了

k短路可以A*,能MLE呢

咕咕咕函数

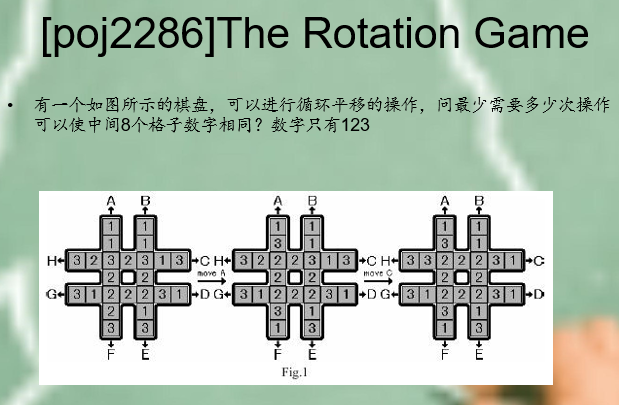
A*是8-最多的格子个数

状态无限所以要ID

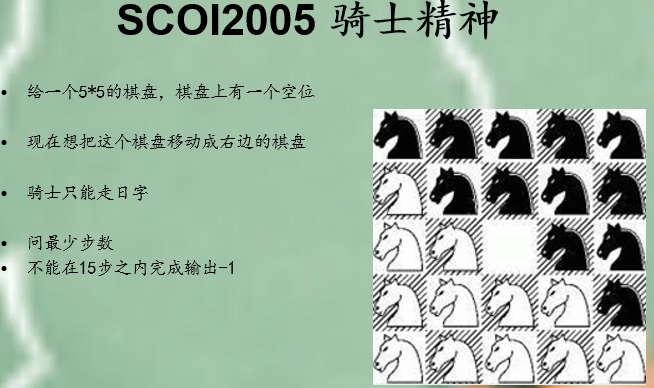
我们又有无限个状态

估价函数是有多少位置不同-1

然后这个东西是因为最后一步可以还原两个棋子

题目告诉我们要枚举答案QAQ

不显然可以折半

把方案折半,前12种的有一些,前13种的有一些

然后考虑三个人的数如何快速判断相等

第一个搜索中三个人的和我们可以两个做差,然后得到一个大小为2的差分数组

然后考虑拼在一起的时候是要第二个从右向左差分去查

显然可以手写哈希表来查存

爬山即可

每次向所有方向中能降低权值最小的走

可以考虑一个呜噜呜噜的判断方向做法

就是所有向量求和?的和向量方向

模拟退火

设置一个棒棒的估价函数

然后一个降温温度

然后一个可能跳出去的判断方法

$exp(delta/T)>rand()/RAND_MAX$T值越小这个里面的值绝对值越大,而del显然是负数,那么del越小越容易交换

同样的,如果我们最大化,只需要变一下符号即可

整数划分

钦定前面大于后面

屑

背包问题

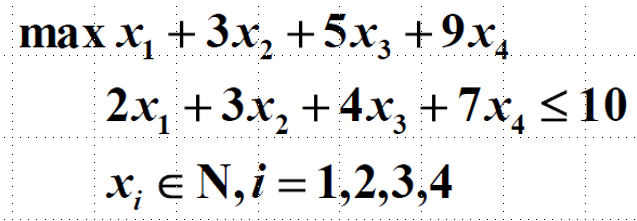
可以考虑按照性价比排序进行搜索,这样容易剪枝

因为性价比是递减的,如果当前性价比下(买小数个)凑出的答案都不够优秀就return

货郎担

状压可以解决20了

直接搜还是蛮难的...

背包问题

所以下一个面额是什么可以搜索出来

然后我们拼一拼的时候可以背包来做.....看不能延伸

奇偶最短路的实现方法就是每个点拆成奇数点和偶数点然后连边随便连一连

最后只有一个源点出发跑一跑bfs最短路就行了

整除

奇数

$a+b|(a^n+b^n)$

偶数

$(a+b)|(a^n-b^n)$

总-不合法

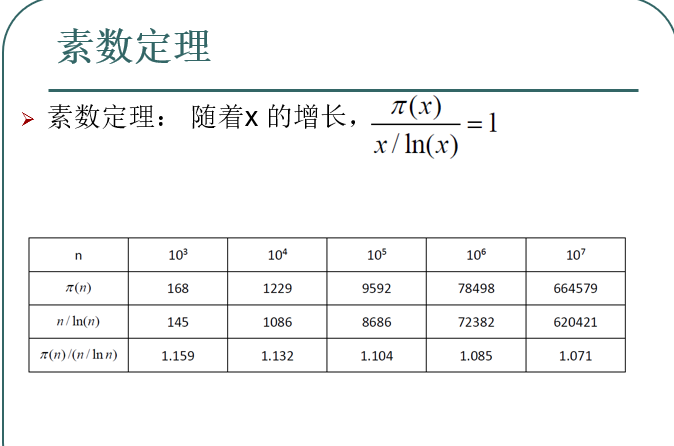
推推石子得到

$\sum_{i=1}^n {i/gcd(i,n)}$

$\sum_{d|n} \sum_{k=1}^{n/d} {k*[gcd(k,n/d)==1]}$

$\sum_{d|n}\sum_{k=1}^{n}k*[gcd(k,n)=1]$

后面这个式子显然是phi函数可以做到的

显然i与n互质,n-i与n互质

所以所有和n互质的数的和为$\phi(d)*d/2$

做完了,可以预处理最小质因数做到log

$\sum_{d|n}n/d\sum_{i=1}^n[gcd(i,n)==d]$

$\sum_{d|n}n/d\sum_{i=1}^{n/d}[gcd(i,n/d)==1]$

$sum_{d|n}d\phi(d)$

卢卡斯定理

$C(n,m)$

n用m进制分解,然后各位的数对应求组合数然后相乘???

gcd,lcm

gcd二除法

b=0,gcd=a

1. 两数都为偶数

$=2*gcd(a/2,b/2)$

2. 二数都为奇数

$=gcd(a-b,b)$

3. 一奇一偶

$=gcd(a/2,b)$

多元一次方程输出方案

显然我们考虑如果能前n-1个构造出和第n个数剩余系下所有数就能表示M

然后这个条件就是互质

显然因为我们所有数和最后那个数互质也就是说我们n-1的情况还可以继续变小

具体构造起来可能是O(nlogn)的....

中国剩余定理

$N=\prod_{i} m_i$

$c_i=N/m_i$

$K_i*c_i=1 (mod m_i)$

$x=\sum_{i=1}^n a_ic_iK_i$

正确性显然

有人想生成函数?

考虑插板法可以计算没有n限制下的解

有限制可以容斥

那么我们考虑至少一个$x_i>n$很好算,只需要k-n即可

然后我们钦定有多少大于n,k就减去多少个n

设i维的j维面有f个,然后转移会发现一条线能成为一个面,而一个面能成为两个面

即i-1维的j维元素*2,j-1维元素成为j维元素...

$f_{i,j}=f_{i-1,j}*2+f_{i-1,j-1}$

规律不好找/jk