多省省选联考全真模拟考试1

http://csp.ac/contest/9

考场上其实有点爆炸,T2的部分分可以多拿一点?

但总体来说切掉T1就还行吧

豆豆手里有一些数字可重的集合。一个集合S的优美值定义为：最大的x，满足对于任意i∈[1,x]，都存在一个S的子集S'，使得S'中元素之和为i。

现在豆豆要考察你的OI水平：

给定n个集合，对于每一次询问，指定一个集合S1和一个集合S2，以及一个数k，要求选择一个S2的子集S3(|S3|≤k)，使得S1∪S3的优美值最大。（集合元素可以重复）

考虑对于 $[1,now)$ 这个范围我们已经覆盖好了

然后加入一个新数x,如果 $x<now$ 那么新范围一定是 $[1,now+x)$ 否则这个x无法加入集合

所以做法就显而易见了,我们先尽量在S1里面选取,实在选不了了我们再去S2中选个最优的,再去看看一集合

企鹅国的货币体系很奇怪，一共有 $N$ 种面值不同的硬币，每种硬币都有无限个，而且任意两个硬币 $(x,y)$ ,满足 $x$ 要么是 $y$ 的倍数，要么就是 $y$ 的因数。

现在豆豆想要去银行取 $M$ 元钱，他想知道他有多少种取硬币的方法。两种方法不同，当且仅当存在某个面值的硬币的个数在两种方案中不同。

暴力是可以直接背包,然后还有一档部分分是可以直接找规律的

正解...我们先转化题意变为你在爬山,每次可以向上跳 $v_i$ 而且这一次的距离要小于上一次的,问总方案数?

这个东西如果你贪心的想,每次跳最大的,然后把这个过程经过的位置标红,那么这些位置就一定会被每一种方案经过

因为一种方案本质不同的前提是使用金币数量不同那么我们对于 1 3 9 27 M=54

第一个27无论你开始时跳9还是跳3都一定会被经过

那么关键点和关键点之间的方案数是可以乘起来的...矩阵乘法?

设 $dp[i][j][k]$ 表示第一步为 $v_j$ ,最后一步大于等于 $v_k$ ,一共走了i步总方案数,走的步数权值先排个序

然后考虑转移,枚举中间一步走的是啥

dp[i][j][k]=\sum_{a}dp[a][j][p]*dp[i-a][p][k]

这个式子一看就是矩阵乘法的形式,也就是说我们只需要用矩乘算出关键点(这样可以倍增啊),然后就做完了

另外一种解法是 $f_i$ 表示只用i种 $v_i$ 拼出x方案数,那么这个东西是一个 $i-1$ 次多项式,可以把关键点用DP求解出来,然后插值吗??不太懂qwq

齐神还有 $n^3$ 做法%%%

这个真的是构造题了

首先我们可以状压DP记录选了那些城堡,然后到了交点i,j转移时枚举下一步去哪,注意这个dp是有环的,所以我们要把dp状态图建出来然后跑最短路

其次60%有一个结论就是每个城堡到左上方的城堡的最短路一定被河流包围了

证明...否则一定不会更优

所以这就点醒我们要把最短路树建出来,然后正解呼之欲出?

...想多了,正解是最短路....

我们把原网格图中每个交点拆成4个点,然后把最短路树经过的每个边删除掉,再在这个图左上方主城位置两个点一个向右一个向左连边跑最短路就好了

就是这样一张图,绿线代表最短路:

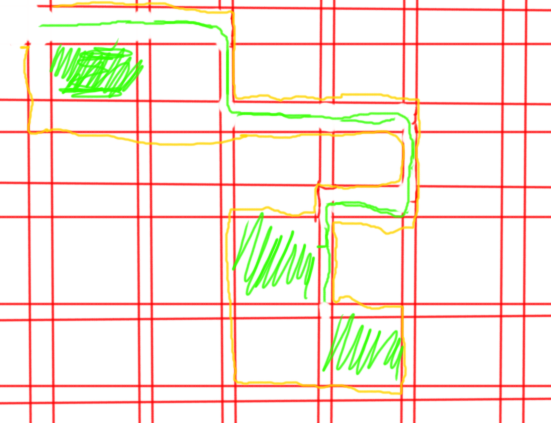
完结散花!

夏晓光(loveJY)的博客