回文自动机(PAM)详解
后宫里的自动姬越多越好啊
回文自动机是记录了字符串中所有回文子串的一类自动机
基础
结论1:字符串中本质不同回文子串不超过个
考虑数学归纳
当的时候,s只有一个字符,同时只有一个子串,此子串回文,结论成立
当的时候,我们假定前个字符组成的字符串成立,对于加入第个字符,新产生的回文中心假设为l,从小到大排序后,对于最小的回文中心,以他为中心可以将所有回文中心大于他的字符串翻折都能找到一个前S字符组成的子串,所以不会存在多个字符增加的情况,因此每次新增加一个字符 本质不同回文子串只会增加1个
因此状态数是的,而且不会超过上界
构造方法
初始建立两个根1,0,代表奇长度和偶长度回文串,满足:
len[0]=0;
len[1]=-1;
fail[0]=1;
fail[1]=0;
lst=0;
T=1;
即奇长度偶长度互指,而且
然后扩展一个字符考虑增量构建,首先找到前S个字符形成的最长回文后缀lst,然后对于加入c
我们首先找到lst的一个最长回文后缀p满足该后缀前一个字符是c,然后从改字符出发,如果存在加入c后形成的回文子串,则无需新建节点,否则新建T节点,长度为p的+2,然后求出新节点的fail,只需要在p节点的fail上重新找最长回文后缀即可,最后令p节点加入字符c得到的串为T,然后lst为T
int get_fail(int x) {
while(s[ln - len[x] - 1] != s[ln])
x = fail[x];
return x;
}
inline void ins(int c) {
int p = get_fail(lst);
if(!ch[p][c]) {
len[++T] = len[p] + 2;
int tmp = get_fail(fail[p]);
fail[T] = ch[tmp][c];//可能为0
ch[p][c] = T;
}
lst = ch[p][c];
}
不难发现此过程复杂度为,和sam相同,每次我们向上跳对应只会有一次向下走的操作
应用
P3649 [APIO2014]回文串
建立PAM,对于每次新加入节点,将对应新lst
然后统计fail树上和即可
PAM和SAM不同,在拓扑dp的时候只需要从后向前统计即可,因为PAM保证父节点标号小于子节点,无论是fail树还是PAM上
P4762 [CERC2014]Virus synthesis
设计dp即可
表示最后一次操作为加字符/翻倍,能得到的最少操作次数
对于PAM转移,我们会发现只有加字符一种,但是如果上次操作为翻折,那么我们可以先加入一个字符再翻折,否则只能加入两个字符
另外的两类转移是从最长回文后缀加字符过来,或者从长度小于一半的后缀走到一半再翻折,这个维护个fail2指针即可
CF17E Palisection
直接Manacher数点是区间加区间查询...不一定能冲过去
否则我们可以PAM吗
还真可以啊,可以正难则反,统计所有没有交集的回文串个数
这样的回文串个数左端点一定在某个右端点之前,也就是插入x,统计所有左端点在x之后的回文串个数,前缀和后缀和就做完了
最小回文划分
这个比较牛逼
问题是给出一个字符串,想让你找到最小的k,满足存在一种方案将s划分为为回文串
考虑朴素的dp,
显然一个字符串可以有个回文子串,T了
记字符串长度为i的前缀为
然后我们有周期以及border的数学定义,但是只要记住周期+border=|S|即可
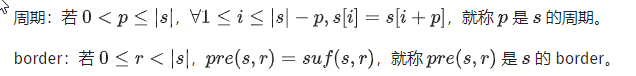
周期和border的关系就是如果t是s的border,那么就是s的周期
证明:
由周期推border太简单了
border推周期我们只需要观察定义可知是,因此p就是
引理1:t是回文串s的后缀,t是s的 border 当且仅当t是回文串。
当t是border的时候一定是回文串,因为我们能发现
然后(回文串)就能以此方法推出所有s字符相同了
同时如果是回文串,我们可以同样的转移相等位置,得到
引理2:t是回文串s的border (),s是回文串当且仅当t是回文串。
s是回文串时由引理1显然成立
当t是回文串的时候,因为,所以我们至少有字符串一半的位置可以使用引理1的证法得到对应相等,也就是一定回文了
引理3:t是回文串s的 border,则|s|-|t|是s的周期,|s|-|t|为s的最小周期,当且仅当t是s的最长回文真后缀。
该引理无需证明,最小周期需要最长border,而最长border就是最长回文真后缀引理4:x是一个回文串,y是x的最长回文真后缀,z是y的最长回文真后缀。令u,v分别为满足x=uy,y=vz的字符串,则有下面三条性质(uy表示连接两个字符串uy)
-
-
,有
-
,有
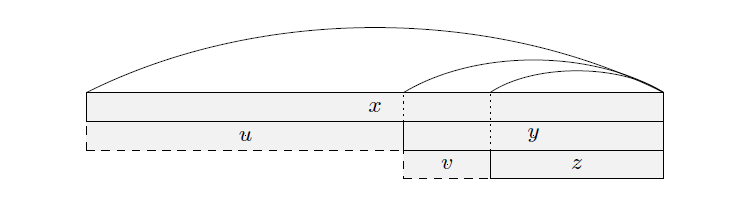
证明
- 考虑引理3的推论,v是y的最短周期,u是x的最短周期,因为y是x的一个后缀,所以u也是y的一个周期,而如果,我们能发现和v是最短周期,矛盾,因此结论成立
- 如果
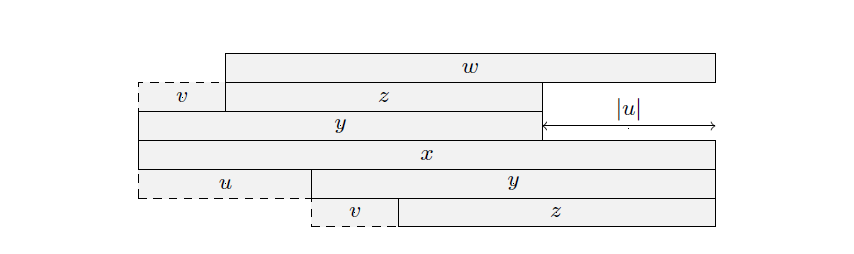
根据下图我们可以得知,即,不难发现w长度超过 ,也就是说w为回文串(引理2),就有w为x的border,于是这和x的最 小周期为u矛盾,故结论不成立
- u,v都可以通过翻折变为x的前缀,两者必然相等
推论:s所有回文后缀按长度排序后可划分为段等差数列
证明
将所有回文后缀按照长度排序,如果任意,则其构成等差数列,否则我们可以知道
由于引理4,我们有
此时引理4的2成立,即
所以有