二维计算几何基础...

点的表示

很basic

需要支持两点对应单位向量叉积,两点对应的单位向量点积,两点坐标直接相减,两点坐标直接相加,使用结构体封装

struct nd {
	db x, y;
	nd(db X = 0, db Y = 0): x(X), y(Y) {};
	db operator^(const nd &x) {
		return this->x * x.y - this->y * x.x;
	}
	db operator*(const nd &x) {
		return this->x * x.x + this->y * x.y;
	}
	friend nd operator-(nd a, nd b) {
		return nd(a.x - b.x, a.y - b.y);
	}
	friend nd operator+(nd a, nd b) {
		return nd(a.x + b.x, a.y + b.y);
	}
	nd operator*(db w) {
		return nd(this->x * w, this->y * w);
	}
};

c++98可过

向量/直线两点式表示

调用上述nd定义来定义即可

我们只需要实现两向量叉积和点积

但是实际写的时候一般用三个点叉积更多不说了

还需要实现极角排序,对于不同的题目第二个return内容不同,如果要保留所有直线逆时针方向的半平面,可以使用以下模板

struct rec {
	nd a, b;
	rec(nd A = nd(0, 0), nd B = nd(0, 0)): a(A), b(B) {};
	db operator^(const rec &x) {
		return (this->b - this->a) ^ (x.b - x.a); //没有交换律
	}
	db operator*(const rec &x) {
		return (this->b - this->a) * (x.b - x.a);
	}
	friend bool operator<(rec x, rec y) {
		db t1 = atan2((x.b - x.a).y, (x.b - x.a).x);
		db t2 = atan2((y.b - y.a).y, (y.b - y.a).x);  // 求极角
		if (fabs(t1 - t2) > eps)                      // 如果极角不等
			return t1 < t2;
		return sign((x.b - x.a) ^ (y.b - x.a)) > 0; // 判断向量x在y的哪边，令最靠左的排在最右边
	}
};

atan2

定义是输入坐标(x,y)

返回(x,y)对应单位向量的极角k,$arctan(k)=\frac{x}{y}$

还是很好用的,实测是先按照x轴负半轴极角从大到小排序,然后x轴正半轴极角从小到大排序

如果我们只需要上凸壳形成半平面,那么只需要按照斜率从高到底排序即可!

两点式求交

属于我们能考场手推的内容

这里给出相似的解法

nd its(rec x, rec y) {//求交点
	nd u = x.a - y.a, v = x.b - x.a, w = y.b - y.a;//三角形
	db t = (w ^ u) / (v ^ w);
	return x.a + v * t;
}

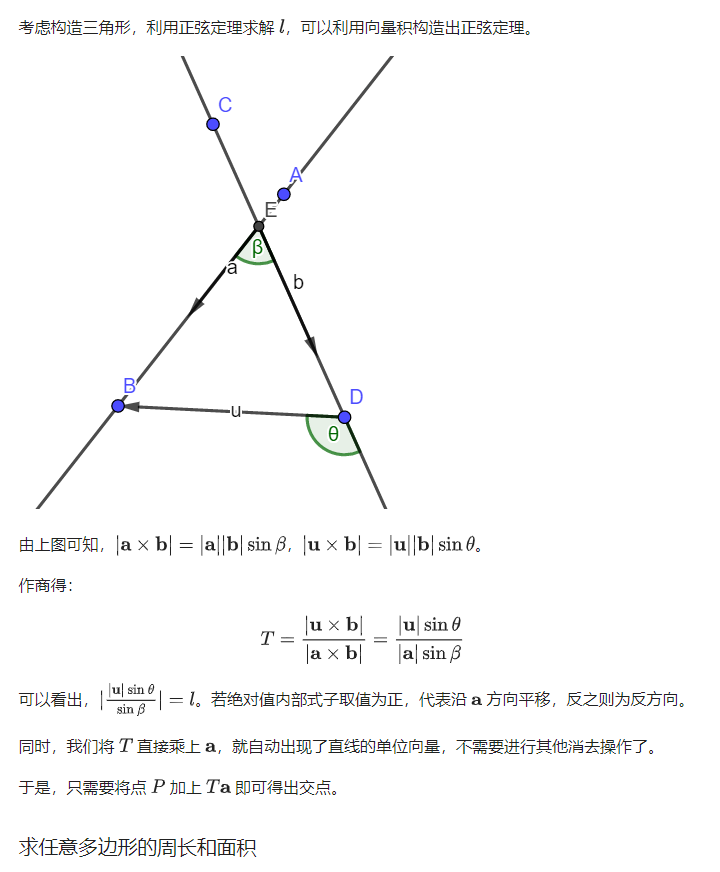
点斜式求交点更简单,就不写了

叉积

判断一条直线在另一条直线的某一侧神器

对于$A X B$,当其大于0时说明A在B的右侧,否则在B的左侧

这个判断方法很简单,我们画出A,B向量,然后用右手放在A向量处向B握,当大拇指向纸面里则说明叉积小于0,否则说明大于0

判断点在线段上

这个是不错的套路啦...

首先叉积可以判断点是不是在直线上,等于0说明在直线上

然后用哪个点和线段两端点求点积,如果得到结果大于0,说明两点在这个点同侧,就不在线段上,反之就在

多边形求面积

三角剖分

选取一个顶点,然后加上每个三角形有向面积即可,这样凹多边形也能求

inline void solve2() {
	db ans = 0;
	for(int i = 2; i < num; ++i) {
		ans += (p[i] - p[1]) ^ (p[i + 1] - p[1]);
	}
	printf("%.3lf\n", ans / 2.0);
}

半平面交

极角排序,然后依次加入

根据题目特性,我们要放弃一些极角相同的线段!在本题中只需要保留最靠左的

一条新插入的线段,如果右侧的交点在这个线段的右侧,对于左半平面交就没用了

又因为我们加在头尾都有可能,所以还要判断头

然后最后我们可能用头去删掉尾尾干掉头因此要聪明一点点

直接维护即可

inline void solve() {
	sort(v.begin(), v.end());
	int l = 1, r = 0, cnt = 0;
	for(int i = 0; i <= n - 1; ++i) {
		if(!sign(getang(v[i].b - v[i].a) - getang(v[i + 1].b - v[i + 1].a)))continue;
		L[++cnt] = v[i];
	}
	L[++cnt] = v[n];
	for(int i = 1; i <= cnt; ++i) {
		while(l < r && onright(L[i], q[r], q[r - 1]))r--;
		while(l < r && onright(L[i], q[l], q[l + 1]))++l;
		q[++r] = L[i];
	}
	while(l < r && onright(q[l], q[r], q[r - 1]))--r;
	while(l < r && onright(q[r], q[l], q[l + 1]))l++;
	num = 0;
	for(int i = l; i <= r; ++i)
		p[++num] = its(q[i], q[i + 1]);
	p[++num] = its(q[r], q[l]);
	return ;
}