夏晓光(loveJY)的博客

C

被切爆了

首先两边同时除d

$b_i'+b_j'+1=b_i'b_j'$

$b_i'$与$b_j'$

然后会发现如果已知$b_j'$可以解出唯一的$b_i'$

然后$b_i'=\frac {b_j'+1} {b_j'-1}$

当且仅当$b_j$为3的时候有整数解$b_i'$

所以可以直接发现,一个b序列排序后相邻的数就是/2*3找到下一个数...

如果没有下一个数就gg了,统计序列中所有这样合法的链的和即可

1.注意相同的数可以一起放进序列中

2.注意某数出现次数*权值最大的那个也可能成为答案

#include<iostream>
#include<cstdio>
#include<cstring>
#include<map>
#include<algorithm>
#define int long long
using namespace std;
#define ll long long
const int MAXN = 4e5 + 7;

int n, a[MAXN], vis[MAXN];
ll sum;
map<int, int> mp;

inline void init() {
	ll tmps = 0;
	for(int i = n - 1; i >= 0; --i) {
		tmps += a[i + 1];
		if(a[i] != a[i + 1]) {
			sum = max(sum, tmps);
			tmps = 0;
		}
	}
}

signed main() {
	// freopen("test.in", "r", stdin);
	// freopen("test1.out", "w", stdout);

	scanf("%lld", &n);
	for(int i = 1; i <= n; ++i) {
		scanf("%lld", &a[i]);
	}
	sort(a + 1, a + n + 1);
	init();
	for(int i = 1; i <= n; ++i) {
		mp[a[i]] ++;
	}
	ll tmps = 0, nw = 0;
	for(int i = 1; i <= n; ++i) {
		if(mp[a[i]] != 0) {
			tmps = mp[a[i]] * a[i];
			if(a[i] % 2)continue;
			nw = a[i] * 3 / 2;
			while(mp.find(nw) != mp.end()) {
				tmps += mp[nw] * nw;
				mp[nw] = 0;
				if(nw % 2)break;
				nw = nw * 3 / 2;
			}
			sum = max(sum, tmps);
		}
	}
	printf("%lld\n", sum);
	return 0;
}

D

构造题

$x_i=-1$

直接前n/2的和后n/2的连边即可

答案也可以这样算,让最小的那个最后删,然后$n/2rank$的第一次删这样子...

也就是说让大数的贡献尽量小!

$x_i!=-1$

分三类讨论:

1.无解

当且仅当所有连向最大的或者所有其他的连向次大的次大的连向最大的

其他情况一定有解

2.前n/2的x不相同

一定可以前n/2的和后n/2的连边解决

也就是说答案和$x_i=-1$一样啊

输出方案的时候要注意一下,可以后面的去找前面的连边,但是要从后面限制最大的开始找...

3.前n/2的x相同

也就是说前n/2的和后n/2的不能直接连边配对了

这样我们随便找到大于n/2的能和那个数配对的最小数然后把它和那个数配对

然后剩下m-1个数变成了$x_i=-1$的情况

细节在于能不能找到/xyx

解决了...qwq

#include<bits/stdc++.h>
#define ins insert
#define mkp(x,y) (make_pair(x,y))
#define fi first
#define se second
// #define int long long
#define ll long long
const int MAXN = 6e5 + 7;
using namespace std;

priority_queue<pair<int, int> > heap;
vector<int> v[MAXN];
set<int> st;
struct ball {
	int x, v, id;
	bool operator<(const ball &x)const {
		return v < x.v;
	}
} a[MAXN];

int n, ans[MAXN], vis[MAXN];
ll  Ans;

inline int pd() {
	int flg = 1;
	for(int i = 1; i < n; ++i) {
		if(a[i].x != a[n].id) {
			flg = 0;
			break;
		}
	}
	if(flg)return 1;
	for(int i = 1; i < n - 1; ++i) {
		if(a[i].x != a[n - 1].id) {
			return 0;
		}
	}
	if(a[n - 1].x == a[n].id)return 1;
	return 0;
}

int que[MAXN];
inline int solve1() {
	if(n == 2)return 0;
	for(int i = 2; i <= n / 2; ++i)
		if(a[i].x != a[i - 1].x || a[i].x == -1)
			return 0;
	int tmp = a[1].x;
	pair<int, int> ans3;
	for(int i = n / 2 + 1; i <= n; ++i) {
		if(a[i].x != tmp && a[i].id != tmp && a[vis[tmp]].x != a[i].id) {
			ans3 = mkp(a[i].id, tmp);
			Ans += min(a[i].v, a[vis[tmp]].v);
			break;
		}
	}
	int h = 0;
	for(int i = n / 2; i <= n; ++i) {
		if(a[i].id != ans3.fi  && a[i].id != ans3.se) {
			que[++h] = a[i].id;
		}
	}
	for(int i = n / 2 - 1; i >= 1; --i) {
		Ans = Ans + 1ll * a[i].v * (n / 2 - i + 1);
	}
	printf("%lld\n", Ans);
	printf("%d %d\n", ans3.fi, ans3.se);
	for(int i = n / 2 - 1; i >= 1; --i) {
		printf("%d %d\n", a[i].id, que[h--]);
	}
	return 1;
}

signed main() {
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i)scanf("%d", &a[i].v);
	for(int i = 1; i <= n; ++i)scanf("%d", &a[i].x), a[i].id = i;
	sort(a + 1, a + n + 1);
	for(int i = 1; i <= n; ++i)vis[a[i].id] = i;
	if(pd())return puts("-1"), 0;
	for(int i = 1; i <= n / 2; ++i)
		if(a[i].x != -1)
			v[vis[a[i].x]].push_back(a[i].id);
	if(solve1())return 0;
	for(int i = 1; i <= n / 2; ++i) {
		Ans = Ans + 1ll * a[i].v * (n / 2 - i + 1);
	}
	for(int i = n / 2 + 1; i <= n; ++i) {
		heap.push(mkp(v[i].size(), i));
	}
	for(int i = 1; i <= n / 2; ++i) {
		st.ins(a[i].id);
	}
	for(int k = n / 2 + 1; k <= n; ++k) {
		int i = heap.top().second;
		heap.pop();
		int M = v[i].size();
		for(int j = 0; j < M; ++j) {
			if(!ans[v[i][j]]) {
				st.erase(v[i][j]);
			}
		}
		auto qwq = st.begin();
		ans[(*qwq)] = a[i].id;
		st.erase(qwq);
		for(int j = 0; j < M; ++j) {
			if(!ans[v[i][j]]) {
				st.ins(v[i][j]);
			}
		}
	}
	printf("%lld\n", Ans);
	for(int i = n / 2; i >= 1; --i) {
		printf("%d %d\n", a[i].id, ans[a[i].id]);
	}
	return 0;
}

E

brute

第一步预处理,改变枚举方式和预处理子函数

考场人类智慧:发现分子分母可以分开计算,分别使用nlnn,然后就省去了快速幂的log!

分子分母分开计算,分别整除分块可以O(nloglogn).看我抄PPT

$y^{d(y)}=\prod _{z|y}y=\prod_{z|y}z*y/z=\prod_{z|y}z^2$

原式子

$\prod_{x=1}^t\prod_{y|x}\prod_{z|y}\frac {z^2} {(z+1)^2}$

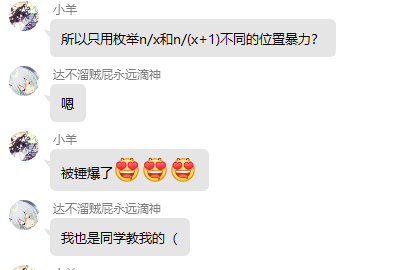
还是交换下求和顺序

首先减少一个x

$s=\prod_{y}^n \prod_{z|y} (\frac {z} {z+1})^{\lfloor \frac n y \rfloor}$

这个东西会发现我们还可以进一步减少求和符号!

$y'=yz$

$\prod_{z=1}^n \prod_{y'=1}^{\frac n z}(\frac z {z+1})^{\lfloor \frac{n }{y'z}\rfloor}$

这一步我们就再整除分块变形

$\prod{z=1}^n(\frac {z} {z+1})^{\sum_{y'=1}^{n/z} \frac {n/z} {y'} }$

显然这个东西可以做到$O(n^{3/4})$了QAQ....

问我为什么,我只能说整除分块威武!

然后呢?如果我们精通一点数学分析复杂度,可以先预处理$n^{2/3}$左右的约数个数和,然后再把剩下的$n^{1/3}$整除分块

嗯...我好像在口胡,首先指数我们可以发现$\frac{n/z} {y'}$变化的值最多有根号n个,也就是说如果他们指数取值是相同的一段,底数之间会连乘消掉,只剩下$(l/r+1)$那么底数连续一段也很好求了

所以直接对指数整除分块即可

预处理约数个数和这个东西需要线性筛,

设num[i]表示质因子的次数

显然我们有$d_=\prod{num_j+1}i$

再钦点num为最小质因子的次数

所以对于$i \in prime$

$num_{i}=1$

对于$i|prime_j$

$num[i*prime_j]=num_i+1$

而$d_{i*prime_j}=d_i/(num_i+1)*(num_i+2)$

对于$i|\prime_j$

d为积性函数

而$num[i*prime_j]=1;$

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN = 1e7 + 7;
ll t, P, tot, n;
int pri[MAXN], isp[MAXN], f[MAXN], num[MAXN];

inline int add(int &x, ll y) {
	x += y;
	if(x > y)x -= P;
	return x;
}

inline void init() {
	f[1] = 1;
	for(int i = 2; i <= n; ++i) {
		if(!isp[i]) {
			isp[i] = 1;
			pri[++tot] = i;
			f[i] = 2;
			num[i] = 1;
		}
		for(int j = 1; j <= tot && i * pri[j] <= n; ++j) {
			isp[i * pri[j]] = 1;
			if(i % pri[j] == 0) {
				num[i * pri[j]] = num[i] + 1;
				f[i * pri[j]] = f[i] / (num[i] + 1) * (num[i * pri[j]] + 1);
				break;
			} else {
				f[i * pri[j]] = f[i] * 2;
				num[i * pri[j]] = 1;
			}
		}
	}
	for(int i = 1; i <= n; ++i) {
		f[i] = (f[i] + f[i - 1]) % (P - 1);
		// printf("%d %d\n", i, f[i]);
		// printf("%d %d?\n", i, f[i]);
	}
}

inline ll ksm(ll x, int y, int P) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

inline ll getans(ll N) {
	if(N <= n)return f[N];
	ll l = 1, r = 1, res = 0;
	for(; l <= N; l = r + 1) {
		r = N / (N / l);
		res += 1ll * (r - l + 1) * (N / l) % (P - 1);
		res %= (P - 1);
	}
	// printf("%lld\n", res);
	return res;
}

int main() {
	scanf("%lld%lld", &t, &P);
	n = pow(t, 0.666);
	// printf("%d\n", n);
	init();
	ll ans = 1;
	ll l = 1, r = 1, tmp = 0, tmp2 = 0;
	for(; l <= t; l = r + 1) {
		r = t / (t / l);
		tmp = getans(t / l);
		tmp2 = 1ll * l * ksm(r + 1, P - 2, P) % P;
		ans = 1ll * ans * ksm(tmp2, tmp, P) % P;
	}
	printf("%lld\n", 1ll * ans * ans % P);
	return 0;
}

F

原本是lxl的题??

枚举每条边是否出现,然后求环套树森林最大值

meet in the middle?

怎么合并呢?

所有边选中概率相等

不妨补集转换

要么在一个有环的连通块,要么两个端点所在连通块有环

$f_{i,S}$,$g_{i,S}$表示选择i条边后S中点的子图是连通图/树方案数

最后如何维护?

首先滚动数组

决定选择还是不选择,选择就要枚举S,T表示两个端点的方案数

g的方案数注意第一次加入非树边不能*2转移

注意f,g会使得方案数少乘2^{kv},kv表示两边都在V点集的...

subtask4

边权从大到小排序再和subtask3一样即可qwq

附赠文字版题解:

洛谷 8 月月赛 II 题解汇总。

考虑到回放暂时打不开，所以已将讲评 PPT 和源码上传至百度网盘，需要者自取。

链接：link，提取码 yc4a。

A. 造房子 - By pigstd

题意简述：现有 $a$ 个材料 A，$b$ 个材料 B 和 $c$ 块钱，造第 $i$ 层楼需要 $i$ 个 A 材料和 B 材料。 每块钱都可以用来买 $1$ 个材料 A 或 B。求出最多能建多少层楼。

其中 $0\leq a,b,c\leq 10^{12}$。

• 对于前 $20\%$ 的数据：$c=0$。

  直接枚举层数即可。

  如何枚举？

  从小到大枚举层数 $i$，用等差数列求和公式求出当前需要 $\frac{i\times(i+1)}{2}$ 个材料 A 和材料 B，如果没有这么多材料，那么只能建 $i-1$ 层。

  当然，如果不会等差数列求和公式，也可以用变量统计当前所需的材料个数，每次循环的时候将该变量增加 $i$ 即可。

  下文中令 $a,b,c$ 同级，则时间复杂度为 $O(\sqrt{a})$。

• 对于 $40\%$ 的数据：$a,b,c\leq 10^3$。

  可以枚举用多少钱买材料 A，那么剩下来的就全部买材料 B，然后枚举层数即可。时间复杂度 $O(a\sqrt{a})$。

• 对于 $100\%$ 的数据：无特殊限制。

  因为材料 A,B 本质上是相同的，所以不妨令 $a\leq b$（若 $a>b$ 交换一下 $a,b$ 即可），然后分类讨论，如果 $a+c\leq b$，那么这 $c$ 块钱肯定都要花在材料 A 上。

  否则一定有 $a+c>b$，那么先花 $b-a$ 块钱，让材料 A 的个数等于材料 B 的个数，然后 $a,b$ 各加上 $\lfloor\frac{c-(b-a)}{2}\rfloor$，最后枚举层数即可。时间复杂度 $O(\sqrt{a})$。

  std：https://www.luogu.com.cn/paste/tkrgltgq。

  如果直接贪心，对于每一块钱买数量较少的材料（若数量相同则买任意一个材料都可以），那么时间复杂度为 $O(a)$，只能通过 $60\%$ 的测试数据。

• Bonus 1：根据贪心策略求出 A,B 材料最终有多少个后，不难发现有一个临界值 $pos$ 使得不小于 $pos$ 的层数都可以建造，而大于 $pos$ 的层数都无法建造，所以二分出这个 $pos$ 即为答案，时间复杂度 $O(\log a)$。

• Bonus 2：题目还可以 $O(1)$ 求出答案，有兴趣的同学可以自行尝试，此处不作讲解。

B. 排列 - By pigstd

题意简述：从一些数中选出若干个数 $x_1,x_2,\cdots,x_p$（$p$ 为数的个数）满足 $p\ge 2$ 且：令 $y_i=x_{i+1}-x_i$（特别的，$y_p=x_1-x_p$），如果把 $y_1$ 到 $y_p$ 按 $y_1,y_2,\cdots,y_p$ 的顺序排成一圈，那么每两个相邻的数互为相反数且绝对值都为 $k$。

求出所有合法的数列中，所有数之和的最大值。若没有合法的数列输出 $\texttt{NO}$。

输入格式为：先给出 $n,k$，再给出 $n$ 条信息 $a_i,b_i$，表示有 $b_i$ 个 $a_i$。 需要注意的是，题目不保证 $a_i$ 互不相同，若有 $a_i$ 相同则累加其个数计算。

其中，$1\leq n,b_i\leq 10^6$，$0\leq k,a_i\leq 10^6$。

在输入时统计每个数的出现次数。下文中，记 $s_i$ 为 $i$ 的出现次数。

• Subtask 1：保证无合法的数列。

  显然答案为 $\texttt{NO}$。

• Subtask 2：$k=0$。

  因为 $k=0$，所以选出的数列中所有数必须相同。

  因此，枚举值域内的所有数 $c$（即满足 $0\leq c\leq \max a_i$ 的所有 $c$），若 $s_c\ge 2$（注意是不小于 $2$，若出现次数为 $1$ 不满足 $p\ge 2$ 的条件），则可以选择 $s_c$ 个 $c$ 并更新答案，即 $ans\gets \max(ans,c\times s_c)$。

• Subtask 3：$n=1$。

  若 $k\neq 0$ 或者 $b_1<2$ 则答案为 $\texttt{NO}$，否则答案为 $a_1\times b_1$。

接下来直接讲正解。

• Subtask 6：无特殊限制。

  先把 $k=0$ 的情况按照 Subtask 2 的解法特判掉，那么有 $k\neq 0$。

  因为 $y_d=-y_{d+1}\ (1\leq d<p-1)$，所以 $x_{d+1}-x_d=-(x_{d+2}-x_{d+1})$，即 $x_d=x_{d+2}$。\textbf{也就是说，选出来的数列中奇数下标的数相等，偶数下标的数也相等}。

  不妨设奇数下标的数为 $a$，偶数下标的数为 $b$，因为 $y_i$ 的绝对值为 $k$，所以 $a-b$ 的绝对值也为 $k$。

  枚举 $a$，不妨设 $a<b$，那么 $b=a+k$。

  因为最多能选出 $\min(s_a,s_b)$ 个 $a$ 和 $b$，所以对于每一个 $a$，答案为 $(a+(a+k))\times \min(s_a,s_b)$，即更新答案 $ans\gets\max(ans,(2a+k)\times \min(s_a,s_b))$。

  std：https://www.luogu.com.cn/paste/uqftbpg6。

C. GCDs & LCMs - By Alex_Wei

题意简述：从一个长为 $n$ 的序列 $a$ 中选出一个子序列 $b$ 满足：对于所有不为最大值的 $b_i$ ，总有 $b_j$ 使得 $b_j>b_i$ 且 $b_i+b_j+\gcd(b_i,b_j)=\mathrm{lcm}(b_i,b_j)$，求子序列所有数之和的最大值。

其中 $1\leq n\leq 3\times 10^5$，$1\leq a_i\leq 10^9$。

• Subtask 1：$n\leq 2$。

  当 $n=1$ 时答案为 $a_1$，当 $n=2$ 时如果 $a_1+a_2+\gcd(a_1,a_2)=\mathrm{lcm}(a_1,a_2)$ 或者 $a_1=a_2$，那么答案为 $a_1+a_2$，否则为 $\max(a_1,a_2)$。

• Subtask 2：$n\leq 17$。

  枚举 $a$ 的所有子集并判断是否合法。可以预处理出所有合法对 $(i,j)$ 满足 $a_i+a_j+\gcd(a_i,a_j)=\mathrm{lcm}(a_i,a_j)$。时间复杂度为 $O(2^nn^2)$。如果不预处理时间复杂度为 $O(2^nn^2\log a_i)$，较难通过。

• Subtask 4：$n\leq 3\times 10^3$。

  枚举所有 $i,j$ 使得 $i<j$ 且 $a_i+a_j+\gcd(a_i,a_j)=\mathrm{lcm}(a_i,a_j)$，将所有这样的 $i,j$ 之间连一条边，最后求出连通块里所有点的权值之和的最大值即可。时间复杂度 $O(n^2\log a_i)$。

  Subtask 3 可以类似 Subtask 4 枚举权值，时间复杂度 $O(\log a_i\max a_i^2)$。

• 接下来我们证明一个非常重要的结论：对于任意 $x,y$ 满足 $x<y$ 且 $x+y+\gcd(x,y)=\mathrm{lcm}(x,y)$，总有 $x=\frac{2}{3}y$。

  证明：当 $x=y$ 时，原式不成立，所以 $x<y$。

  因为 $x<y$，$\gcd(x,y)<y$，所以 $x+y+\gcd(x,y)<3y$。

  又因为 $x+y+\gcd(x,y)>y$ 且 $\mathrm{lcm}(x,y)$ 是 $y$ 的整数倍，所以 $x+y+\gcd(x,y)=2y$，即 $\mathrm{lcm}(x,y)=2y$。

  因为 $x\times y=\gcd(x,y)\times \mathrm{lcm}(x,y)$，所以 $x\times y=2y\times \gcd(x,y)$，得到 $\gcd(x,y)=\frac{x}{2}$。

  带回原式得到 $x+y+\frac{x}{2}=2y$，解得 $x=\frac{2}{3}y$。

• 根据上述结论，对于每个偶数 $x$，满足 $x+y+\gcd(x,y)=\mathrm{lcm}(x,y)$ 且大于 $x$ 的 $y$ 有且只有一个，即 $y=\frac{3}{2}x$。而奇数则不存在这样的 $y$。

  我们很容易得出，如果将选出来的数从小到大排序，去重，一定满足 $b_i=\frac{2}{3}b_{i+1}\ (1\leq i<k)$。

• Subtask 7：无特殊限制。

  因此，$O(n)$ 枚举最小值就能确定整个序列 $b$，二分或用 map 实现在 $O(\log a_i)\ /\ O(\log n)$ 的时间内查找一个数在序列 $a$ 中的出现次数，并且记录一个数是否被计算过。

  每个数最多只会被计算一次，总时间复杂度：二分 $O(n\log a_i)$，map $O(n\log n)$，不过 map 常数更大一点。

  std：https://www.luogu.com.cn/paste/1m2k3kw4。

  值得注意的是，如果不判断一个数是否被计算过，那么时间复杂度可能会退化成 $O(n\log n\log a_i)$，只能通过 Subtask 5。

• Subtask 6 是给不会二分或 map 的参赛者准备的部分分。

D. Snow Mountain - By ET2006

题意简述：给定两个长为 $n\ (2|n)$ 的序列 $a,x$，满足 $a_i$ 互不相同且如果 $x_i \neq -1$，那么 $a_{x_i}>a_i$。现在需要进行 $\frac{n}{2}$ 次删除操作：选择两个未被删除的数 $a_i,a_j$ 满足 $x_i\neq j$ 且 $x_j\neq i$，并用 $\min(a_i,a_j)\times k$ 的代价将这两个数从序列 $a$ 中删去（删除后剩余元素下标不变），其中 $k$ 表示这是第 $k$ 次删除。求删除所有数的最小代价与方案。若有多种方案输出一种即可。

其中 $2\leq n\leq 5\times 10^5$，$1\leq a_i\leq 10^9$。

下文中记 $m=\frac{n}{2}$。

• Subtask 1：$n=2$。

  如果 $x_1=2$ 或 $x_2=1$，那么答案就是 $-1$，否则答案为 $\min(a_1,a_2)$。

• Subtask 2：$n\leq 10$。

  枚举全排列暴力即可，时间复杂度 $O(n!n)$。

• 结论 1：

  设第 $i$ 次删除的数的编号分别为 $x_i,y_i$，记 $c_i=\min(a_{x_i},a_{y_i})$，那么对于最优删除方案一定满足 $c_i>c_{i+1}\ (1\leq i<m)$，即 $c_i$ 降序。

  这个应该比较好理解，我们证明一下：

  如果 $c$ 并不是降序的，那么因为 $a_i$ 互不相同，一定能找到删除编号 $i,j$ 满足 $i<j$ 且 $c_i<c_j$。

  单独看这两次删除对答案的贡献为 $i\times c_i+j\times c_j$。

  如果交换这两次删除，这时对答案的贡献为 $i\times c_j+j\times c_i$。因为交换两次删除并不会影响其它删除，所以答案的变化量 $\Delta=i\times c_j+j\times c_i-(i\times c_i+j\times c_j)=(i-j)(c_j-c_i)$。

  因为 $i<j$ 且 $c_i<c_j$，所以 $(i-j)(c_j-c_i)<0$，即 $\Delta<0$。

  也就是说，对于 $c$ 中任意的两次删除 $i,j$ 满足 $i<j$ 且 $c_i<c_j$，交换这两次删除总能使答案变得更小，即变优。

  因此，最优方案中 $c$ 一定降序排列。

• Subtask 3：$x_i=-1$。

  对摧毁的水晶没有限制。将能量值排序之后，第 $i$ 小的和第 $m+i$ 小的配对，最后按照结论 1 将 $c$ 降序排列即可。

• 结论 2：

  如果存在一个数 $a_i$ 满足无法和剩下 $n-1$ 个数中的任何一个配对，那么无解。

  正确性显然。

  判断是否无解，根据结论 2，我们可以写出以下算法：令 $deg_i$ 表示 $i$ 号水晶不能够与多少个水晶配对。对于 $x_i \neq -1$ 的 $i$，令 $deg_i\gets deg_i+1$，$deg_{x_i}\gets deg_{x_i}+1$，最后判断是否存在 $deg_i=n-1$，若存在则无解。

• 结论 3：

  如果不满足结论 2，则一定有解。

  • 因为所有情况都能够通过一定转化变为 $a_i$ 单调递增的情况，所以我们不妨设 $a_i$ 单调递增，即 $a_i<a_{i+1}\ (1\leq i<n)$。

  • 结论 3.1：

    若存在两个位置 $i,j\ (1\leq i\neq j\leq m)$ 满足 $x_i\neq x_j$，或者存在一个位置 $i\ (1\leq i\leq m)$ 满足 $x_i=-1$，那么前 $m$ 个数和后 $m$ 个数一定能一一配对删除，取到最小代价。

    • 不妨设位置 $i$ 与 $i+m$ 配对，此时我们找到所有不符合题意（即 $x_i=i+m$）的 $i$，记做 $b_1,b_2,\cdots,b_{cnt}$。

    • 当 $cnt\ge 2$ 时，我们将所有不符合题意的 $b_i$ 与它配对的位置的关系 “旋转” 一下。即对于所有 $b_i\ (1<i\leq cnt)$，将 $b_i$ 配对的位置变为原来 $b_{i-1}$ 配对的位置（即 $b_{i-1}+m$），而 $b_1$ 配对的位置则变为原来 $b_{cnt}$ 所配对的位置（即 $b_{cnt}+m$）。

      例如当 $n=6$，$x_1=4$，$x_2=5$，$x_3=6$ 时，对应关系是这样的：

      

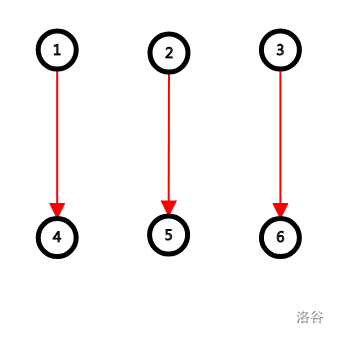
      显然不符合题意。但是如果我们将对应关系 “旋转” 一下，就会变成这样：

      

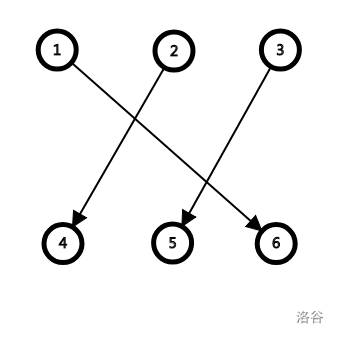
      这样就不会产生冲突，符合题意了。

    • 当 $cnt=1$ 时，因为存在 $x_i\neq x_j\ (1\leq i\neq j\leq m)$，所以一定有一个位置 $pos\ (1\leq pos\leq m)$ 满足 $x_{pos}$ 不等于 $b_1$ 所配对的位置（即 $b_1+m$）。此时交换 $b_1$ 与 $pos$ 所配对的位置即可。

    • 当 $cnt=0$ 时配对关系已经符合题意。

    • 又因为前 $m$ 个数已经是 $a_i$ 中最小的数了，所以每个 $c_i$ 也取到了最小值，降序排列后即为最小代价。

  • 而如果不满足结论 3.1 中的条件，那么一定满足 $x_1=x_2=\cdots=x_m=k\neq -1$。

    从小到大找到第一个可以和 $k$ 配对的数 $k'$，将 $a_k$ 与 $a_{k'}$ 一起删除。由于推论 2.1 中已经判过无解，所以 $deg_k\neq n-1$，也就是说满足条件的 $k'$ 一定存在。

    把 $k$ 解决掉之后，位置 $1,2,3,\dots,m-1$ 就没有了限制。根据贪心的策略，肯定是将前 $m-1$ 个数和后 $m-1$ 个数分别配对。

• Subtask 5：$a_i$ 升序排列。

  根据结论 3 配对，将配对关系根据结论 1 按照 $c_i$ 降序排列即可。

• Subtask 6：无特殊限制。

  首先将 $a_i$ 转化为升序并记录每个数原来的位置，根据结论 3 配对，将配对关系根据结论 1 按照 $c_i$ 降序排列，并根据记录的位置回推每对删除的数在原序列中的位置即可。时间复杂度 $O(n\log n)$。

虽然题解看起来很长，但是大部分都是一些必需的严谨的证明。在比赛中看似证明起来比较复杂的结论却很好猜到并理解。本题同时考察了代码功底和思维水平，是一道不可多得的好题（雾。

std：https://www.luogu.com.cn/paste/x3h8bxm9。

E. 四月樱花 - By SOSCHINA & Muxii

题意简述：求

$\prod_{x=1}^t\prod_{y|x} \frac{y^{d(y)}}{\prod_{z|y}(z+1)^2}$

对 $p$ 取模后的值，其中 $d(y)$ 表示 $y$ 的约数个数，$1\leq t\leq 2.5\times 10^9$，$9.9\times 10^8<p<1.1\times 10^9$ 且 $p\in \mathrm{prime}$。

• Subtask 3：$n\leq 2\times 10^5$。

  暴力 + 预处理。

  • 第一步：改变枚举方式。

    对于一个数 $x$，暴力遍历 $1\sim x$ 每个数并判断其是否为 $x$ 的约数的枚举方式将会造成大量不必要的时间浪费，考虑从约数的角度出发进行遍历。

    具体地说，枚举每个数 $i$，然后枚举 $i$ 的倍数 $i\times j\ (j\geq 1)$，于是 $i$ 为 $i\times j$ 的约数。这样枚举的时间复杂度为 $O(n+n/2+n/3+\cdots+n/n)=O(n\log n)$。

  • 第二步：预处理两个子函数。

    观察式子发现我们可以预处理两个函数，分别为 $f(y)=y^{d(y)}$ 以及 $g(y)=\prod_{z|y}(z+1)$。这样可以避免重复计算。

  • 第三步：计算答案和代码实现。

    时间复杂度为 $O(n\log n)$，实现方式比较多样化，不展开讲。给出一份比较简洁的实现代码：

    https://www.luogu.com.cn/paste/djkt8c1j。

• Subtask 4：$n\leq 2\times 10^6$。

  对于会推式子的同学来说，一个比较显然的想法是将分子分母分开计算。下面分别展示两个式子的化简过程（$d(x)$ 使用线性筛处理）。

  • 分子：$f(n)=\prod_{x=1}^n\prod_{y|x}y^{d(y)}$

    交换 $x$ 与 $y$ 的求和顺序得：$f(n)=\prod_{y=1}^n y^{\lfloor\frac{n}{y}\rfloor d(y)}$

    时间复杂度不太好估计，大概是 $O(n\log \log n)$ 左右。

  • 分母（开平方后的）：$g(n)=\prod_{x=1}^n\prod_{y|x}\prod_{z|y}(z+1)$

    交换 $y$ 和 $z$ 的枚举顺序：$g(n)=\prod_{x=1}^n\prod_{z|x}\prod_{z|y,y|x}(z+1)$

    考虑满足 $z|y$ 且 $y|x$ 的 $y$ 的个数，显然答案为 $d(\frac{x}{z})$。

    $g(n)=\prod_{x=1}^n\prod_{z|x}(z+1)^{d(\frac xz)}$

    再设 $x=x'z$，交换 $x$ 和 $z$ 的枚举顺序：

    $\begin{aligned}g(n)&=\prod_{z=1}^n\prod_{x'=1}^{\lfloor\frac nz\rfloor}(z+1)^{d(x')}\\&=\prod_{z=1}^n(z+1)^{d(1)+d(2)+...+d(\lfloor\frac nz\rfloor)}\end{aligned}$

    可以整除分块，但仍然有 $O(n)$ 计算阶乘的复杂度无法进一步优化。

  代码：https://www.luogu.com.cn/paste/9sbn0deo。

• Subtask 5：$n\leq 10^7$。

  考虑如何整体统一分子分母两个部分。

  设 $f(n)=\prod_{x|n}x=x_1x_2\cdots x_{d(n)}$.

  设 $n=x_iy_i$，于是 $f(n)$ 等价于 $f(n)=\prod_{y|n}y=y_1y_2\cdots y_{d(n)}$。

  将两式逐项相乘得 $f^2(n)=(x_1y_1)(x_2y_2)\cdots (x_{d(n)}y_{d(n)})=n^{d(n)}$。

  即 $n^{d(n)}=\prod_{x|n}x^2$。

  代回原式即得 $s=\prod_{x=1}^n\prod_{y|x}\prod_{z|y}(\frac z{z+1})^2=(\prod_{x=1}^n\prod_{y|x}\prod_{z|y}\frac z{z+1})^2$。

  经过一系列化简（具体过程可以参考 Subtask 4 解法中的分母部分化简方法）得：

  $s=(\prod_{z=1}^{n}(\frac z{z+1})^{S(\lfloor\frac nz\rfloor)})^2$

  其中 $S(n)$ 表示 $d(n)$ 的前缀和。整除分块处理上式即可，但线性筛的时间复杂度无法进一步优化。总时间复杂度为 $O(n)$。

  代码：https://www.luogu.com.cn/paste/97izrhm8。

• Subtask 6：$n\leq 10^8$。

  由 Subtask 5 的解法我们得到式子：$f(n)=\prod_{x=1}^n\prod_{y|x}\prod_{z|y}\frac z{z+1}$。

  之前是从右向左化简，我们这次考虑从左向右化简。

  交换 $x$ 和 $y$ 的枚举顺序：$f(n)=\prod_{y=1}^n\prod_{z|y}(\frac z{z+1})^{\lfloor\frac ny\rfloor}$。

  再设 $y=y'z$，交换 $y$ 和 $z$ 的枚举顺序得：

  $\begin{aligned}f(n)&=\prod_{z=1}^n\prod_{y'=1}^{\lfloor\frac nz\rfloor}(\frac z{z+1})^{\lfloor\frac n{y'z}\rfloor}\\&=\prod_{z=1}^n(\frac z{z+1})^{\sum_{y'=1}^{\lfloor\frac nz\rfloor}\lfloor\frac{\lfloor\frac nz\rfloor}{y'}\rfloor}\end{aligned}$

  然后套两次整除分块即可，积分证明这样做的时间复杂度为 $O(n^{\frac 34})$。

  代码：https://www.luogu.com.cn/paste/dsu23xxy。

• Subtask 7，8：无特殊限制。

  回到 Subtask 5 的那个式子 $s=(\prod_{z=1}^{n}(\frac z{z+1})^{S(\lfloor\frac nz\rfloor)})^2$。

  猜想 $d(n)$ 的前缀和 $S(n)$ 能够使用杜教筛预处理，而事实上也是可行的。

  利用 $d=1\times 1$ 两边同时卷上 $\mu$ 得 $d\times\mu=1\times1\times\mu=1\times\varepsilon=1$

  于是带入杜教筛的递推式得：

  $\mu(1)S(n)=\sum_{i=1}^n1(i)-\sum_{i=2}^n\mu(i)S(\lfloor\frac ni\rfloor)$

  即 $S(n)=n-\sum_{i=2}^n\mu(i)S(\lfloor\frac ni\rfloor)$。

  只需用杜教筛同步筛出 $\mu$ 和 $d$ 的前缀和即可。总时间复杂度为 $O(n^{\frac 23})$。

  std：https://www.luogu.com.cn/paste/mn1vg1al。

F. 寒妖王 - By 平泽唯

题意简述：给定一张 $n$ 个点 $m$ 条边的图。第 $i$ 条边有权值 $w_i$。定义一个边集是好的，当且仅当将这些边和与这些边相连的点取出来形成的图没有两个或以上处在同一个连通块不同的环。同时定义一个边集的权值为边集中所有边的边权之和。求出在每条边有 $50\%$ 的概率消失的情况下，图中权值最大的好边集的权值的期望在模 $998244353$ 意义下的结果。

其中 $1\leq n\leq 15$，$1\leq m\leq 60$，$1\leq w_i<998244353$。

• Subtask 1：$n\leq 10$，$m\leq 20$。

  枚举每条边是否出现，然后求环套树森林的最大值。

  具体的方法是考虑环套树森林的求法和最大生成树类似，把边按照边权从大到小排序，如果当前的边选取之后仍然合法，那么就选取他，否则跳过这条边。

  不难发现这样一定是最优的，证明过程和 Kruskal 算法求最小生成树类似。用并查集判断当前边选取之后是否合法，时间复杂度 $O(2^m m \log n)\sim O(2^m m \alpha (n))$。

  代码：https://www.luogu.com.cn/paste/pl68py0b。

• Subtask 2：$n\leq 10$，$m\leq 30$。

  考虑在 Subtask 1 的做法上改进，使用 Meet in the middle 算法枚举图的前 $\frac{m}{2}$ 条边和后 $\frac{m}{2}$ 条边，然后合并两边的信息。时间复杂度 $O(2^{\frac m 2}n)$。

• Subtask 3：所有边的权值均相等。

  因为每条边的权值是一样的，所以可以随意按照一个顺序选择，直接对第 $i$ 条边考虑它能被选中的概率，显然这和它之前的 $i-1$ 次挑边有关。

  不妨补集转换，如果一条边不能被选择，要么它处于一个含有环的连通块内，要么它的两个端点所在的连通块含有环，我们考虑两个状态 $f_{i,S}, g_{i,S}$ 分别表示选择 $i$ 条边后点集 $S$ 中的点的子图是连通图 / 树的方案数，那么选择 $i$ 条边后点集 $S$ 中点的子图含有环的连通块的方案数就是 $f_{i,S} - g_{i,S}$。

  这样我们可以枚举这条边所在的连通块点集 $V$，方案数是 $\sum f_{i,V}-g_{i,V}$，然后枚举这条边两端所在的点集 $S, T\ (S \cap T=\varnothing,S \cup T=V)$，方案数是 $\sum (f_{i,S} - g_{i,S})\times (f_{i,T} - g_{i,T})$。

  • 最后就是如何维护 $f, g$ 的问题。

    因为求方案数仅和当前边数 $i$ 的 $f_{i,V}$ 有关，所以不难用滚动数组优化掉 $i$ 这一维。

    考虑每次加入一条边，我们就更新 $f_V, g_V$，其中 $V$ 为所有包含这条边的两个端点的点集。需要注意的是如果使用滚动数组，那么先枚举的 $V$ 不应包含于后枚举的 $V$。

    首先包含这条边的 $f_V$ 可以决定选择或者不选择，那么将其乘以 $2$，即 $f_V\gets f_V\times 2$，然后考虑这条边连通两个连通块的方案数，即枚举这条边两端所在的点集 $S,T$ 满足 $S \cup T=V$，$S\cap T=\varnothing$，那么 $f_V\gets f_V+f_S\times f_T$。

    维护 $g$ 的过程类似，只是第一个加入一条非树边的转移不能使用（即 $g_V$ 不能像 $f_V$ 一样一开始乘以 $2$），其余的均相同。

    对于每条边，求方案数的时间复杂度为 $O(3^{n-2})$（其实是 $O(3^n)$ 带上一个 $\frac 19$ 的小常数），更新 $f,g$ 的时间复杂度也为 $O(3^{n-2})$，故总时间复杂度为 $O(m 3^{n-2})$。

    需要注意的是，这样维护 $f,g$ 会使方案数少乘上 $2^{k_V}$，其中 $k_V$ 表示当前（添加 $i$ 条边后）有 $k_V$ 条边满足两个端点都在点集 $V$ 中，所以每条边求出方案数后求期望只需要除以 $2^{i-k_V}$（而不是 $2^i$）。每次添加一条边时可以 $O(2^{n-2})$ 维护 $k$。

• Subtask 4：无特殊限制。

  考虑 Subtask 1 和 Subtask 3 结合，我们只需要先将边按照边权从大到小排序（即固定加入边的顺序），再使用和 Subtask 3 一样的算法即可。时间复杂度 $O(m 3^{n-2})$。

  std：https://www.luogu.com.cn/paste/pl68py0b。