"爱蜜莉雅碳真是天使!"

昴竭尽全力的赞美着爱蜜莉雅

P3185 [HNOI2007]分裂游戏

显然的是,我们每一次只能操作一颗石子

那么把每个石子看成一个游戏,那么我们答案就是所有石子的sg值异或和

怎么定义一颗石子的sg值?

想一个简单化的问题(钟神讲过?),每个石子只能移动到编号比他大的一个石子堆处

那么这个情况下我们相当于每个石子的sg值为其编号....因为相当于每个石子代表一个石子堆,然后减少/增加编号只是拿走一些石子罢了

回到这个题,如果学过Multi-SG,这个问题和上述问题等价啊

但是没有QAQ....于是乎我们先研读一下Multi-SG

Multi-SG问题

有n堆石子，两个人可以从任意一堆石子中拿任意多个石子(不能不拿)或把一堆数量不少于2石子分为两堆不为空的石子，没法拿的人失败。问谁会胜利

怎么求解sg函数值啊?

还是考虑sg(x)表示有x个石子的堆的sg值是多少,然后我们考虑转移相当于枚举我们用哪个操作,以及每个操作如何划分

sg(n)=mex\{\sum_k^{n-1}{sg(k)},\sum_j^{k-1}{sg(j) xor sg(n-j)}\}

啥子意思呢?第一部分很显然吧,就是操作1

第二部分是我们考虑枚举划分为哪些和哪些,然后产生的两个独立游戏求一个异或得到总游戏局面的异或值,这个值就是我们n的后继局面sg值

所以说所有求个mex即可

打表找规律可以发现:

$if x \mod 4 \equiv 0$

sg(x)=x-1

$if x \mod 4 \equiv 1|2$

sg(x)=x

$if x \mod 4 \equiv 3$

sg(x)=x+1

(嗯??为什么第一个会变小啊,因为第三个变大了啊!)

回到本题,发现可能问题和multi-sg的sg值并不等价

因为本问题我们的两个后继数可以自由选择

所以我们可以考虑激情 $n^3$ 枚举进行取mex

得到每个位置一颗石子的sg值后(就是multi-sg中石子堆的)异或起来即可

关于mulit-sg后续会讲的会讲的


#include<bits/stdc++.h>
using namespace std;
const int MAXN = 105;
int T, n, a[MAXN];
int mex[MAXN], sg[MAXN];

inline void solve() {
	memset(mex, 0, sizeof(mex));
	memset(sg, 0, sizeof(sg));
	for(int i = n; i >= 1; --i) {
		for(int j = i + 1; j <= n; ++j) {
			for(int k = j; k <= n; ++k) {
				mex[sg[j]^sg[k]] = i;
			}
		}
		while(mex[sg[i]] == i)sg[i]++;
	}
	//第一次操作合法,当且仅当操作完之后异或值为0呢qwq
	int ans = 0, cnt = 0, flg = 0;
	for(int i = 1; i <= n; ++i)if(a[i] & 1)ans = ans ^ sg[i];
	for(int i = 1; i <= n; ++i) {
		for(int j = i + 1; j <= n; ++j) {
			for(int k = j; k <= n; ++k) {
				if(a[i] && ((ans ^ sg[i]^sg[j]^sg[k]) == 0)) {
					if(!flg) {
						printf("%d %d %d\n", i - 1, j - 1, k - 1);
						flg = 1;
					}
					cnt += flg;
				}
			}
		}
	}
	if(cnt)
		printf("%d\n", cnt);
	else printf("-1 -1 -1\n0\n");
}

int main() {
	scanf("%d", &T);
	while(T-- > 0) {
		scanf("%d", &n);
		for(int i = 1; i <= n; ++i)scanf("%d", &a[i]);
		solve();
	}
	return 0;
}

P2594 [ZJOI2009]染色游戏

二维翻硬币,感觉毛估估一下就不会做,看了一眼部分分会40%,暴力搜索.....

先来搞一维翻硬币吧

一维翻硬币

N 枚硬币排成一排，有的正面朝上，有的反面朝上.

每次我们可以进行满足某些限制的翻转操作,把一些硬币翻转,但是最右边的那个硬币必须是从正面翻转到反面,谁不能翻动谁输

约束条件一：每次只能翻一个硬币

答案和n的奇偶性有关

证明?显然

约束条件二：每次能翻转一个或两个硬币(不用连续)

开始放火了啊

还是想办法定义一个sg值,但是要先划分一下游戏局面

一个神仙的想法就出现了,每个正面朝上硬币就是一个游戏,显然独立,而且最后我们也都要翻转为反面

那么一个硬币的信息就和他的位置有关了, $sg(i)$ 表示位置为i正上的sg值

不妨假设两次操作中i是编号最大的那个(?),如果只进行一次操作,我们假设另外一次是操作了0位置

于是我们发现如果第二次操作,相当于把i这个正上的位置向前移动,

什么意思呢?如果我们正上为1,反上为0,那么你会发现相当于每次操作就是给这个位置-1,给之后某个位置+1,这就意味着其实就是把一颗石子向前搬动了!

如果把它看成在nim中每个石子堆%2意义下的移动,就会更清楚

于是? $sg_i=i$ ,做完啦!

约束条件三：每次必须连续翻转k个硬币

首先来学习一个经典套路,博弈论打表法....

$K=3$

啥东西呢? $sg_i$ 还是表示有i个硬币,只有最后一个正面朝上的sg值

为啥对的呢?因为你想我们是一次翻转多个而不是一个,所以状态的设计子游戏的划分就不能够单独一个硬币

同时有一个最好的好处,我们依然满足总局面相当于每个子局面sg值异或和

因为我们对于后续状态的影响还是对于2取模的,所以说经典的sg定理跳后继永远还是成立的

再看看转移

N=1,正,必败为 $sg_1=0$

N=2,反正,必败为 $sg_2=0$

N=3,反反正,必胜为 $sg_3=1$

N=4,反反反正,反正正反,子游戏局面为sg=0^1=1,必败为 $sg_4=0$

依次按照这个方式打表下去

001001001001......

每k个一个1,其余均为0,我们证明一下?即如果k的倍数的位置正上出现了奇数次先手必胜

剩余偶数个

此时无论如何操作,我们下一步一定k倍数位置会变成奇数个

否则不能操作,必败

剩余奇数个

我们选择为k倍数位置最后的那个硬币操作一次,一定能确保奇数位置-1变为偶数,丢给对方偶数局面,然后对方就会拿到一个偶数局面,要么gg要么再丢回来一个奇数局面

证比,也是为什么sg函数值如此的原因

约束条件4：每次翻动一个硬币后，必须翻动其左侧最近三个硬币中的一个，即翻动第x个硬币后，必须选择x-1，x-2，x-3中的其中一个硬币进行翻动，除非x是小于等于3的,此时可以翻动或不翻动第二个硬币。（Subtraction Games）

还是打表先

我们每次翻转操作是两个,所以可以使用之前的定义, $sg_i$ 表示位置为i的正上棋子sg值

N=1,必胜, $sg_1=1$

N=2,必胜, $sg_2=2$

N=3,必胜, $sg_3=3$

N=4,发现我们要么转移到1,要么转移到2,要么是3, $sg_4=0$

N=5, $sg_5=1$

SG:123012301230.....

啊这,好像和之前的case完全一样,就不证明了...

约束条件5：每次必须翻动两个硬币，而且这两个硬币的距离要在可行集S={1,2,3}中，硬币序号从0开始。(Twins游戏)

每次必须翻动两个使得 $sg_1=0$ (必败)

$sg_2=1$

$sg_3=mex(sg_2,sg_1,sg_0)=2$

$sg_4=mex(sg_3,sg_2,sg_1)=3$

012301230123.....

和前一个都一模一样,除了开场1暴毙外

约束条件6：每次可以翻动一个、二个或三个硬币。（Mock Turtles游戏）

牛逼

其实还是直接打表,这里能翻转3个的话其实直接按照两个子游戏局面异或起来就好....

$sg_1=1,sg_2=2$

也就是说 $sg_2$ 值为

$mex(1,2,0,3)$

位置从0开始

1 2 4 7 8 11 13 14 16 19 21 22 25 26 28

oeis

"Nim-values for game of mock turtles played with n coins. "

??????

自食其力:

当2x二进制形式1个数为奇数,sg值为2x,否则为2x+1,也就是下一个odious数

??????

我们称二进制形式1个数为奇数的为odious,否则为evil

那么我们有如下牛逼的东西

evil^evil=odious^odious=evil

evil^odious=odious^evil=odious

发现这个之后,就起飞了

你会发现,无论如何我们使用一次操作都能得到所有较小的odious数,而那些大于他的odious数都不能够

因为odious和odious异或只能得到evil,我们能够得到足够多的evil,(甚至大于2x的),但是绝对得不到下一个odious

故以这种形式的sg值永远是下一个odious数

其实还需要证明为什么这个是对的....感觉难跳了

**约束条件7：每次可以连续翻动任意个硬币，至少翻一个。（Ruler游戏）

(这是和本题唯一有关的...)

$sg_i=lowbit(i)$

/jk?其实很简单,我们还是按照之前位置i的方式定义sg值,于是我们就有

sg_n=mex{sg_0,sg_{n-1},sg_{n-1}^sg_{n-2}.......,sg^{n-1}^...^sg_{1}}

还缺一步证明

约束条件8：每次必须翻转4个对称的硬币，最左与最右的硬币都必须是从正翻到反。（开始的时候两端都是正面）（Grunt游戏）

/jk...不太会

回到本题

$if(i==1||j==1)$

sg_{i,j}=lowbit(i+j-1)

$else$

sg_{i,j}=2^{i+j-2}

哇偶,看上去和对角线有关系,但是又去掉了边界,有人用数学归纳法证明了一下,感觉价值不大

拓展:这个东西可能和曼哈顿距离有关,猜想k维情况下sg值(不算边界)可能是 $2^{\sum_i k_i}$

其中应该要-sth,但是不重要了....只是为了空间连续而已吧???

算上边界的话....应该就降维度这样子,注意一维降成lowbit???

可能是因为降成下一维度吧?所以qwq了



#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-(x)))
using namespace std;
const int MAXN = 300;
int T, n, m;
int f[MAXN], mp[MAXN];
char s[MAXN][MAXN];

inline int sg(int x, int y) {
	if(x == 1 || y == 1)return mp[lowbit(x + y - 1)];
	return x + y - 2;
}

int main() {
	scanf("%d", &T);
	for(int i = 0; i < 9; ++i)mp[1 << i] = i;
	while(T-- > 0) {
		scanf("%d%d", &n, &m);
		for(int i = 1; i <= n; ++i)scanf("%s", s[i] + 1);
		for(int i = 1; i <= n; ++i) {
			for(int j = 1; j <= m; ++j) {
				if(s[i][j] == 'T') {
					f[sg(i, j)] ^= 1;
				}
			}
		}
		bool flg = 0;
		for(int i = 0; i <= n + m; ++i)if(f[i])flg = 1;
		if(flg)puts("-_-");
		else puts("=_=");
		memset(f, 0, sizeof(f));
	}
	return 0;
}

P3235 [HNOI2014]江南乐

可以做惊人70pts, $n^2$ 求sg值,就是考虑对于一个石子堆x,枚举y等分然后xor起来即可,可以用bitset优化???不需要,我们O(n)找sg值应该也可以?

于是我们考虑怎么快速求sg值,这里有一个很妙的记忆化搜索实现方式

因为我们有一个最最重要的性质:

x=\lfloor\frac{n}{m}\rfloor

那么这个x至少是n的一半!

也就是说我们会每次缩小一半问题规模,求解一个1e5的就是 $O(nlogn)$ 的!!!

于是考虑怎么实现,首先我们枚举这个x,因为他只有根号种取值

然后对于一个x,考虑划分后有多少数取到x,有多少数取到x+1

很简单,n%m个取到x+1,其他都是x.....qwq

于是我们发现有n%m个x+1,和m-n%m个x.....

因为n=x*m+n%m......qwq

code:



#include<bits/stdc++.h>
using namespace std;
const int MAXN = 3e5 + 7;
int n, T, F, a[MAXN], sg[MAXN], mex[MAXN], ans;

inline int solve(int x) {
	if(x < F)return sg[x] = 0;
	if(~sg[x])return sg[x];
	sg[x] = 0;
	for(int i = 2; i <= x; i = x / (x / i) + 1) {//m
		for(int j = i; j <= min(i + 1, x); j++) {
			if((x % j) & 1)solve(x / j + 1);
			if((j - x % j) & 1)solve(x / j);
		}
	}
	for(int i = 2; i <= x; i = x / (x / i) + 1) {
		for(int j = i; j <= min(i + 1, x); j++) {
			int r = 0;
			if((x % j) & 1)r ^= solve(x / j + 1);
			if((j - x % j) & 1)r ^= solve(x / j);
			mex[r] = x;
		}
	}
	while(mex[sg[x]] == x)sg[x]++;
	return sg[x];
}

int main() {
	memset(sg, -1, sizeof(sg));
	scanf("%d%d", &T, &F);
	while(T-- > 0) {
		scanf("%d", &n);
		ans = 0;
		for(int i = 1; i <= n; ++i) {
			scanf("%d", &a[i]);
			ans ^= solve(a[i]);
		}
		if(ans)printf("1 ");
		else printf("0 ");
	}
	return 0;
}

P2599 [ZJOI2009]取石子游戏

~~取石子游戏都紫了,江南乐还能黑的??~~

sg定理在本题根本不好用,因为限制是动态变化的,但是动态规划又是个扯淡的玩意,记录左右端点还剩多少个石子?

~~好像能过30分! $1e5^2$ 雾~~

于是我们翻开题解

$L_{i,j}$ 表示区间i,j左边放上一堆个数为 $L_{i,j}$ 的石子后,先手面对这个局面必败

简直神来之作!我们来证明 $L_{i,j}$ 有且仅有一个

不会存在多个

但凡存在,我们选取个数多的合法的那个,操作一步转移到个数少的合法的,先手就必胜了,和状态定义矛盾

一定存在

假设不存在,那么也就是说左边放上任意数量石子先手都必胜

那么先手必然不会去操作左边的,因为无论如何怎么操作都是转移到一个必胜态

先手操作右边那一堆,按照状态的定义此时左边放入多少都是必败态,那么后手在左边随便操作一次,我们就从一个必败态转移到了一个必败态,就矛盾了

于是.....这个状态还真行

求值?我们考虑另一个数组 $R_{i,j}$ 表示区间i,j右边放上一堆个数为 $L_{i,j}$ 的石子后,先手面对这个局面必败

于是就可以来转移啦!

对于 $[i,j-1]$ ,我们要转移 $L_{i,j}$ ,不妨假设 $a_j$ 个数为x

$x=R$

也就是说,我们原区间直接必败了,那么这个区间也要必败,就直接递归入原区间即可

$L=0$

$x<L,x<R$

都小于,也就是说我们右边要转移到必败态是不太可能的,那么我们想先手操作后是个必胜态

令 $L_{i,j}=x!$ ,因为你会发现无论先手怎么操作,后手都可以完全模仿先手的操作,从而一定有一个时间点,某一堆被拿空而我们正好是后手操作

根据sg值此时不可能是0,要么左边剩要么右边剩,而无论左右怎么剩剩下的都要小于对应一遍L/R,那么就是一个必胜态

后手必胜,先手必败

$L<=x<R$

这个相当牛逼了....有一个神仙操作方法,先手可以把后手逼疯

$L_{i,j}=x+1$

先手第一种走法是转移到>L的某个数,此时我们后手肯定可以转移到那个数减1,从而情况仍旧

第二种走法是走到L,那么我们后手一步拿光右边即可(先手就拿到了必败态),如果右边没有石子是不可能的,因为老子是后手

第三种是走到小于L的一个数,那么我们后手一步拿到和你相同即可,因为这样拿下去一定存在某个时刻后手面对一堆空掉的情况呢(nim游戏)

如果先手操作右边?搞笑呢,要么直接照抄case2,要么直接照抄自己

$R<x<=L$

$L_{i,j}=x-1$

想想就知道和3情况完全对偶吧

后手拿右边截杀你就好

$x>L,x>R$

$L_{i,j}=x$ ,sg值为0

要是先手不用L,R点卡我们,直接拿相同的绝杀他

要是先手用L,R点卡我们,我们直接一步拿到x-1或者x+1转移到case3,4即可

$L_{i,i}=a_i$

所以综上所述这样子dp一下就做完了

最后判断 $L_{2,n}$ 是否等于 $a_1$ qwq

这个R真的是对称,理解之后很好写的.....


#include<bits/stdc++.h>
using namespace std;
const int MAXN=2005;
int T,n,a[MAXN];

int L[MAXN][MAXN],R[MAXN][MAXN];

inline void solve() {
	memset(L,0,sizeof(L));
	memset(R,0,sizeof(R));
	for(int len=1; len<=n; ++len) {
		for(int i=1; i<=n-len+1; ++i) {
			if(len==1) {
				L[i][i]=a[i];
				R[i][i]=a[i];
				continue;
			}
			int j=i+len-1;
			if(a[j]==R[i][j-1]) {
				L[i][j]=0;
			} else if(a[j]<L[i][j-1] && a[j]< R[i][j-1]) {
				L[i][j]=a[j];
			} else if(a[j]>=L[i][j-1] && a[j]<R[i][j-1]) {
				L[i][j]=a[j]+1;
			} else if(a[j]>R[i][j-1] && a[j]<=L[i][j-1]) {
				L[i][j]=a[j]-1;
			} else if(a[j]>L[i][j-1] && a[j]>R[i][j-1]) {
				L[i][j]=a[j];
			}
			if(a[i]==L[i+1][j]) {
				R[i][j]=0;
			} else if(a[i]<L[i+1][j] && a[i]<R[i+1][j]) {
				R[i][j]=a[i];
			} else if(a[i]>L[i+1][j] && a[i]>R[i+1][j]) {
				R[i][j]=a[i];
			} else if(a[i]>=R[i+1][j] && a[i]<L[i+1][j]) {
				R[i][j]=a[i]+1;
			} else if(a[i]>L[i+1][j] && a[i]<=R[i+1][j]) {
				R[i][j]=a[i]-1;
			}
//			printf("%d %d %d %d\n",i,j,L[i][j],R[i][j]);
		}
	}
	if(n==1)puts("1");
	else if(a[1]==L[2][n])puts("0");
	else puts("1");
}

int main() {
	scanf("%d",&T);
	while(T-->0) {
		scanf("%d",&n);
		for(int i=1; i<=n; ++i)scanf("%d",&a[i]);
		solve();
	}
	return 0;
}

P6791 [SNOI2020] 取石子

~~我就会第一步问题转换~~

相当于取到倒数第二颗石子的人赢,相当于-1后先取光的人赢,相当于-1后不能操作的人输

然后我们可以设计dp来做10%, $f_{i,j}$ 表示还剩下i个石子,然后上个人走j是否可先手必胜

于是你会发现这个f数组的转移点其实可以写出来!

因为经过观察发现,这个数组的第二维一定满足在一个值之前都是0,之后都是1 qwq

然后打表开始了....


num 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
par 1 2 3 1 5 1 2 8 1 2  3  1  13 1  2

表示前i个石子的时候那个分界点是什么,和fib很像,于是引入fib进制

齐肯多夫定理：任何正整数可以表示为若干个不连续的斐波那契数之和。

那么下面的fib就表示par1在fib进制下的数值

转换的方法就是如果 $n>f_i$ ,直接这位为1,然后 $n-f_i$ ,i--这样子


num 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
fib 1 2 3 1 4 1 2 5 1 2  3  1  6  1  2
par 1 2 3 1 5 1 2 8 1 2  3  1  13 1  2

对着这个东西看，我也不知道为什么可以看出 num 所对应的 par 就是此 num 在斐波那契进制下的表示的最低位的 1 所表示的值。

对于数列 $p$ 的前 $f_i$ 项，由数列的前 $f_{i-1}$ 项与前 $f_{i-2}$ 项接在一起，并且将 $f_i$ 项更改成 $f_i$ 即可。

这个其实就是数列按照斐波那契的形式扩展构造qwq

我们知道了 $p_i$ ，考虑将答案表示出来。

根据 $p_i$ 的定义，答案显然为：

\sum_{i=1}^{N}[k \geq p_i]

既然知道了构造方法，那么定义 $sum(i,j)$ 为，数列 ppp 的前 $f_i$ 项出现了 $sum(i,j)$ 次 $f_j$ 。

根据我们的构造方法，我们可以将其用 $O(\log^2 n)$ 的时间预处理出来所有的 $sum(i,j)$ 。

具体操作就是对于按照fib的形式, $sum_{i,j}=sum_{i-1,j}+sum_{i-2,j}$ ,但是要特判 $i-1==j$ 的情况,也就是最后一项被篡改的情况!

回答询问时，我们先找到最大的 $c$ ，使得 $k \geq p_c$ 并且 $k<p_{c+1}$ 。然后去回答这个问题。

不过找到一位合法的之后再去Olog统计未免太蠢,我们把sum数组按照第二个维度再差分一次

现在的含义变为 $sum(i,j)$ 为，数列 ppp 的前 $f_i$ 项的前 $f_j$ 出现了 $sum(i,j)$ 次。

也就做完啦~~

code:


#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN=205;

ll n,p,T,k;
ll s[MAXN][MAXN],f[MAXN];


int main() {
	f[0]=1;
	f[1]=1;
	int qwq=90;
	for(int i=1; i<=qwq; ++i) {
		f[i+1]=f[i]+f[i-1];
//		printf("%lld\n",f[i]);
		s[i][i]=1;
		for(int j=1; j<=i; ++j) {
			s[i+1][j]=s[i-1][j]+s[i][j]-(j==i-1);
		}
	}
	for(int i=1; i<=qwq; ++i) {
		for(int j=1; j<=qwq; ++j) {
			s[i][j]+=s[i][j-1];
		}
	}
	scanf("%lld",&T);
	while(T-->0) {
		ll ans=0;
		scanf("%lld%lld",&k,&n);
		int p=0;
		while(f[p+1]<=k)++p;
		for(int i=qwq; i>=1; --i)if(n>f[i])n-=f[i],ans+=s[i][p];
		printf("%lld\n",ans);
	}
	return 0;
}

AT1999 [AGC002E] Candy Piles

一种很巧妙的转换形式,灵光一现想到了但是没有深究,看来思路要dfs的进行才行啊!(idfs??)

我们把每个糖果排序后写成网格图的形式,第i列高度为j表示 $a_i=j$

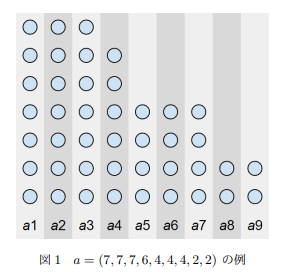
不难发现,每次操作对应了消除一行或者一列,也就等价于我们从原点向上或者向右走一步,那么我们就可以考虑一个简单的等价操作方法:沿着对角线走,因为你向上/向右一步后手一定可以跟着你操作

但是数据范围太大,我们再观察

一个必败点(O)是后继必须存在必胜点(x)

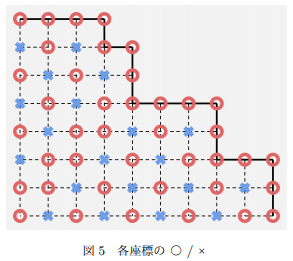
那么可以根据这个图片搞事情啦!

即找到原点相邻两对角线有没有最后能走到必败的??

/晕不太懂

P2490 [SDOI2011]黑白棋

SDOI自己抄自己(雾)

SDOI2019的移动金币很相近吧,这个计数形式好像一模一样

考虑给出一个局面能不能判断谁必胜....

然后一开始读错题自闭半天...以为我们动一个棋子就是只能动一步,实际上可以动许多

一个石子堆大小为相邻黑白的位置差-1

那么这个就变成一个每次能动k堆石子的k-nim

k-nim问题经典结论是每个二进制位在 $%(k+1)$ 意义下加法如果最后能为0则先手必败

证明?很简单吧...只要懂了nim你想想这个也是一样的

然后考虑怎么计数,显然每一位要分开考虑

$dp_{i,j}$ 表示前i位已经考虑,然后当前用了j个石子的满足异或值为0的方案数

转移考虑第i位一下子转移光,枚举一下放 $d+1$ 的多少倍就好(这样异或起来才是0啊)

然后注意的是,我们是第i位,所以用掉了 $(d+1)*x*(1<<i)$ 颗石子!

所以说可以转移了吗/se?我们还是冲个无标号上去,就是先dp出每一堆的形态,然后最后再分配位置

要组合一下选择那些堆数放

dp_{i+1,j+(d+1)*x*(1<<i)}=dp_{i+1,j} * \binom{k/2}{x}

最后

dp_{i,j}=dp_{i,j}*\binom{n-j-k/2}{k/2}

qwq

P3223 [HNOI2012]排队

某中学有 $n$ 名男同学， $m$ 名女同学和两名老师要排队参加体检。他们排成一条直线，并且任意两名女同学不能相邻，两名老师也不能相邻，那么一共有多少种排法呢？（注意：任意两个人都是不同的）

$n,m<=2e3$

好像很好玩,看一眼数据范围自闭了,结果发现是高精,哭啦

老师放在一起

那中间一定要有一个人叉开,钦定他是女生,那么就会发现qwq不能再插入其他空位了

这三个绑起来,有共 $n+1$ 个元素,剩下 $n-1$ 个女生插入n+2个空,直接排列然后排列数进去即可

注意*2,三个元素内部

不放在一起

那么就不能放在一个空

先排列,然后考虑选出两个位置,然后剩下 $n+2$ 个元素,有 $n+3$ 个空位,选出m个空格插入

为什么博弈论里有计数?我也不知道

SP11414 COT3 - Combat on a tree

经典套路了。。。。qwq

做法就是直接求sg值就好， $sg_i$ 表示点i为子树的局面的sg值

求sg值？就是在这个子树里面操作一次求下sg值

相当于枚举子树里面所有的白点，然后删掉，然后从那个白点出发向根dfs，然后路过的所有不经过这个白点到根路径上的点的sg值求个异或，再把所有求异或的数拿出来求个mex即可

如果用个数组维护一下可能就 $O(n^2)$ 了。。。

然后还记得清华集训那道题吗？我们只需要用个01trie即可优化！

考虑过了这个点的影响，其实就是把一些点的01trie整体异或上一个除去这个点儿子外其他儿子的异或值这样子

就是说u->fa,那么所有里面的sg值全异或上这个u的兄弟的sg值异或和

然后如果u是白点，那么要新加入一个点，权值是所有儿子异或和

叶子结点因为不能操作，所有有白点sg值为1，否则为0

01trie要支持：

全局异或
查询mex
快速合并

第三个很好做

全局异或相当于打标记，就是说我们给全局打一个标记，然后直接向线段树一样下推即可

然后查询mex需要维护一个子树siz和，如果子树的siz等于这个点代表的串剩下的所有数，那么mex值肯定大于这个值，就向右走这样子，如果右边也一样就是这个点是答案

实现也有一点细节，就是从高位开始做，然后一开始钦点一下每个串长度,这样我们查mex的时候才知道子树siz的关系

CF1110G Tree-Tac-Toe

一开始秒掉了两种case

一个点度数大于等于4

那此时直接先手选住这个点然后和后手轮流选邻居即可

一个点度数等于3,然后有两个子树大于等于2

最小的单元是六个点,eg:

1->2

2->3

3->4

2->5

2->6

先手选2,后手选3,先手选5,后手选1/6先手选另一个就赢了

然后就没了,于是我也没了

剩下的情况只有三种

链
左边两个点,右边链
左边右边都有两个点,中间链

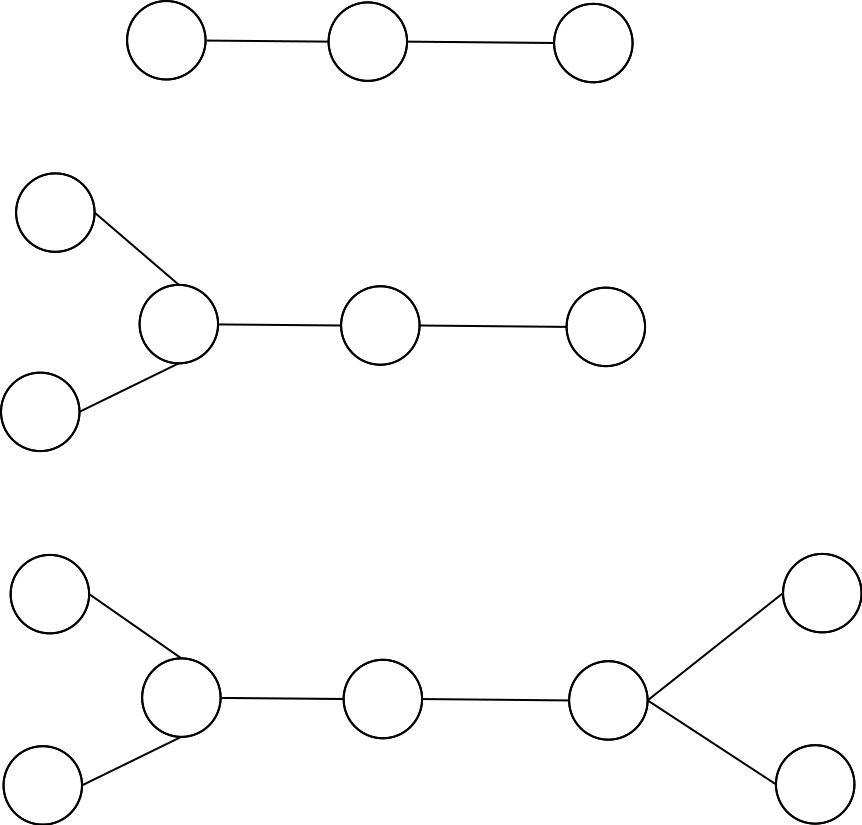
第三种情况当点数为奇数的时候先手也是必胜的,其他的case就真的平局了

怎么证明?不妨给出先手一种操作顺序,使得一定可以按照这个顺序取胜

第一步选择最左边度数为三的点后面那个点

此时后手只能选度数为3,不然立刻死亡

然后你继续选择第一个染的点右边两个点

后手染上空位...

这样下去你一定能染到最右边度数为3的点左边一个点的时候还有先手,直接取胜即可

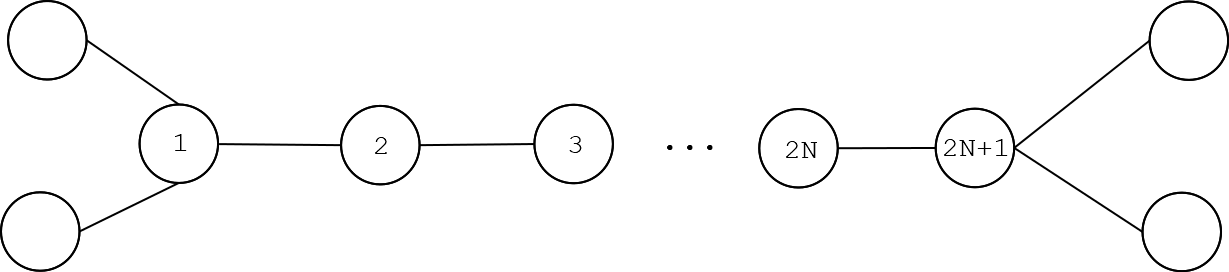
具体的选取编号为2,4,6,8......的点qwq

https://www.luogu.com.cn/training/42936#problems

还有这么个东西没做完

[HNOI2010]取石头游戏

未完待续中

下接:贝尔的数学篇1

夏晓光(loveJY)的博客

昴的博弈论2