某金牌训练营Day13
A
如果只有单点修改,就是设表示值为前一个位置在哪,然后直接树套树单点修改在线的数点即可
现在有区间修改,我们会发现推平了的一段只会和一个数有关,也就是说我们可以把数字相同的段合并,然后左右端点询问扩展到两边界即可
我们就可以把一段他们的信息暴力删掉给两侧,然后你会发现我们每次修改都可以花费删掉个区间,但是至多分裂出两个
现在的区间修改,我们同样发现是几个部分的查询,如果扩展询问边界,就只是一整段的查询了
树状数组套权值线段树即可,复杂是
#include<bits/stdc++.h>
#define vi vector<int>
#define fi first
#define ins insert
#define pb push_back
using namespace std;
const int MAXN = 6e5 + 7;
int n, m, a[MAXN], pre[MAXN], vis[MAXN], rt;
vi v;
struct rec {
int l, r, x;
rec(int L = 0, int R = 0, int X = 0): l(L), r(R), x(X) {};
bool operator<(const rec &w)const {
return l < w.l;
}
} q[MAXN];
inline int getid(int x) {
return lower_bound(v.begin(), v.end(), x) - v.begin() + 1;
}
const int MAXT = 6e7 + 7;
namespace seg2 {
#define mid ((l+r)>>1)
int ls[MAXT], rs[MAXT], T, tr[MAXT];
inline void mdf2(int &k, int l, int r, int p, int w) {
if(!k)k = ++T;
tr[k] += w;
if(l == r)return ;
if(p <= mid)mdf2(ls[k], l, mid, p, w);
else mdf2(rs[k], mid + 1, r, p, w);
}
inline int qry2(int k, int l, int r, int L, int R) {
if(!k)return 0;
if(L <= l && r <= R)return tr[k];
if(R <= mid)return qry2(ls[k], l, mid, L, R);
else if(L > mid)return qry2(rs[k], mid + 1, r, L, R);
else return qry2(ls[k], l, mid, L, R) + qry2(rs[k], mid + 1, r, L, R);
}
}
namespace seg {
int ls[MAXN], rs[MAXN], T, rt2[MAXN];
inline int qry(int k, int l, int r, int L1, int R1, int L2, int R2) {
if(!k)return 0;
if(L1 <= l && r <= R1)
return seg2::qry2(rt2[k], 0, n, L2, R2);
if(R1 <= mid)return qry(ls[k], l, mid, L1, R1, L2, R2);
else if(L1 > mid)return qry(rs[k], mid + 1, r, L1, R1, L2, R2);
else return qry(ls[k], l, mid, L1, R1, L2, R2) + qry(rs[k], mid + 1, r, L1, R1, L2, R2);
}
inline void mdf(int &k, int l, int r, int p, int q, int w) {
if(!k)k = ++T;
seg2::mdf2(rt2[k], 0, n, q, w);
if(l == r)return ;
if(p <= mid)mdf(ls[k], l, mid, p, q, w);
else mdf(rs[k], mid + 1, r, p, q, w);
}
}
set<int> st[MAXN];
set<rec> odt;
inline void init() {
v.pb(0);
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
for(int i = 1; i <= n; ++i) {
a[i] = getid(a[i]);
}
for(int i = 1; i <= m; ++i) {
if(q[i].x != -1)q[i].x = getid(q[i].x);
if(q[i].x != -1)st[q[i].x].ins(0);
}
for(int i = 1; i <= n; ++i) {
pre[i] = vis[a[i]];
vis[a[i]] = i;
st[a[i]].ins(0);
st[a[i]].ins(i);//自闭了
seg::mdf(rt, 1, n, i, pre[i], 1); //插入
odt.ins(rec(i, i, a[i]));
}
return ;
}
//light状态需要满足:
//1. 后继light点能点亮他
//2. 这个点的答案在树套树会产生贡献
//3. 这个set中保留他的信息
//4. 作为odt的一段起点存在
inline void light(int x, int v) {
auto it = st[v].upper_bound(x);
if(it != st[v].end()) {
int p = *it;
seg::mdf(rt, 1, n, p, pre[p], -1);
pre[p] = x;
seg::mdf(rt, 1, n, p, pre[p], 1);
}
pre[x] = *(--st[v].lower_bound(x));
seg::mdf(rt, 1, n, x, pre[x], 1);//觉醒了
st[v].ins(x);
}
inline void dark(int x, int v) {
seg::mdf(rt, 1, n, x, pre[x], -1);
st[v].erase(x);
auto it = st[v].upper_bound(x);
if(it != st[v].end()) {
int p = *it;
seg::mdf(rt, 1, n, p, pre[p], -1);
pre[p] = pre[x];
seg::mdf(rt, 1, n, p, pre[p], 1);
}
}
set<rec>::iterator split(int x) {
if(x > n)return odt.end();
auto it = --odt.upper_bound((rec) {
x, 0, 0
});
if(it->l == x)return it;
int l = it->l, r = it->r, v = it->x;
odt.erase(it);
odt.ins(rec(l, x - 1, v));
light(x, v); //分裂需要
return odt.ins(rec(x, r, v)).fi;
}
inline void assign(int l, int r, int v) {
auto itr = split(r + 1), itl = split(l);
auto it = itl;
for(; it != itr; ++it) {
int p = it->l, w = it->x;
if(p == l) {
dark(p, w);
light(p, v);//点亮他
} else {
dark(p, w);
}
}
odt.erase(itl, itr);
odt.ins(rec(l, r, v));
}
inline int qbel(int x) {
auto it = --odt.upper_bound((rec) {
x, 0, 0
});
return it->l;
}
inline void solve() {
for(int i = 1; i <= m; ++i) {
if(q[i].x != -1) {
assign(q[i].l, q[i].r, q[i].x);
} else {
q[i].l = qbel(q[i].l);
q[i].r = qbel(q[i].r); //查询所属
printf("%d\n", seg::qry(rt, 1, n, q[i].l, q[i].r, 0, q[i].l - 1));
}
}
return ;
}
namespace fastIO {
#define BUF_SIZE (1<<20)
static char buf[BUF_SIZE], *p1 = buf, *pend = buf;
inline char nc() {
if(p1 == pend) {
p1 = buf;
pend = buf + fread(buf, 1, BUF_SIZE, stdin);
}
return *p1++;
}
inline int read() {
int x = 0;
char s = nc();
for(; !isdigit(s); s = nc());
for(; isdigit(s); s = nc())x = (x << 1) + (x << 3) + s - '0';
return x;
}
}
using namespace fastIO;
int main() {
freopen("sequence.in", "r", stdin);
freopen("sequence.out", "w", stdout);
n = read();
m = read();
for(int i = 1; i <= n; ++i) {
a[i] = read();
v.pb(a[i]);
}
for(int i = 1, opt; i <= m; ++i) {
opt = read();
if(opt == 1) {
q[i].l = read();
q[i].r = read();
q[i].x = read();
v.pb(q[i].x);
} else {
q[i].l = read();
q[i].r = read();
q[i].x = -1;
}
}
init();
solve();
return 0;
}
B
一个字符串S的本质不同的回文串个数是级别
不难发现操作2得到的字符串一定是偶回文串
那么我们可以用回文串当做状态,此时因为回文自动机储存了所有本质不同回文子串,所以可以把上面的节点当做回文子串
表示限制最后一步一定是翻转操作,此时原串为s,那么答案是
同时对于S还要取min,但是字符串不是空串,有长度就不用取min,因为单字符一定是奇回文串
然后考虑转移
第一种转移是想要进行操作2
那么要翻转的字符串长度一定要小于目标串的一半
假设最长小于一半的最长回文后缀为
相当于暴力补全然后在翻折一次
为什么只考虑最长?因为我们不需要重复转移,得到的方法和无关,是子问题
然后第二种转移,我们从某一个串暴力加字符得到t
显然是从t的最长回文后缀转移而来,加上
就是
然后第三种转移,就是在某一个串的两端加上字符得到t
这个是从t的PAM的父亲上转移而来,加上1即可,因为我们这一次的翻折操作可以使用他父亲的,改为先加一个字符再翻折
最后问题在于怎么求出第一个转移的t',就是长度小于一般的指针
并不难,我们只需要先继承父亲的指针指向的节点,然后类似kmp的方法,如果长度大于一半就回跳,否则我们停下来,然后看能不能延长一步即可
注意本题卡空间,256mb空间只能开6e7个int自闭了
还有就是清空要小心T和n不同阶可能T大可能n大
然后就是拓扑排序的时候要从1号节点开始,而一号节点他的长度为-1,所以代码里使用指针重定向了数组
#include<iostream>
#include<cstring>
#include<cstdio>
const int MAXN = 6e6 + 7;
using namespace std;
int n;
char qwq[MAXN];
int s[MAXN], a[MAXN], buc[MAXN], dp[MAXN][2], *c;
namespace PAM {
int ch[MAXN][5], fail[MAXN], len[MAXN], f[MAXN];
int lst, T, ln;
void init() {
for(int i = 0; i <= T; ++i) {
fail[i] = len[i] = f[i] = 0;
for(int k = 0; k < 4; ++k)ch[i][k] = 0;
}
len[0] = 0;
len[1] = -1;
fail[0] = 1;
fail[1] = 0;
lst = 0;
ln = 0;
T = 1;
}
int get_fail(int x) {
while(s[ln - len[x] - 1] != s[ln])
x = fail[x];
return x;
}
inline void ins(int c) {
int p = get_fail(lst);
if(!ch[p][c]) {
len[++T] = len[p] + 2;
int tmp = get_fail(fail[p]);
fail[T] = ch[tmp][c];
ch[p][c] = T;
if(len[fail[T]] <= len[T] >> 1) {
f[T] = fail[T];
} else {
int q = f[p];
while((len[q] + 2) > (len[T] >> 1) || (s[ln] != s[ln - len[q] - 1]))q = fail[q];
f[T] = ch[q][c];
}
}
lst = ch[p][c];
}
}
using namespace PAM;
inline void solve() {
c = buc + 1;
for(int i = 0; i <= T; ++i)c[len[i]]++;
for(int i = 0; i <= n; ++i)c[i] += c[i - 1];
for(int i = 0; i <= T; ++i)a[c[len[i]]--] = i;
for(int i = 0; i <= T + 3; ++i)dp[i][0] = dp[i][1] = 0x3f3f3f3f;
dp[1][1] = 0;
dp[0][1] = 0;//是由添加字符转移而来
int ans = 1e9;
for(int i = 3; i <= T + 1; ++i) {
int u = a[i];
dp[u][1] = min(dp[u][1], min(dp[fail[u]][1], dp[fail[u]][0]) + len[u] - len[fail[u]]);
if(!(len[u] & 1))
dp[u][0] = min(dp[u][0], min(dp[f[u]][1], dp[f[u]][0]) + (len[u] >> 1) - len[f[u]] + 1); //无法合并
for(int q = 0; q < 4; ++q) {
if(ch[u][q]) {
dp[ch[u][q]][1] = min(min(dp[u][1], dp[u][0]) + 2, dp[ch[u][q]][1]);//添加字符
dp[ch[u][q]][0] = min(dp[u][0] + 1, dp[ch[u][q]][0]);
}
}
ans = min(ans, min(dp[u][1], dp[u][0]) + n - len[u]);
}
for(int i = 0; i <= max(T, n) + 3; ++i)a[i] = buc[i] = 0;
printf("%d\n", ans);
return ;
}
int main() {
freopen("virus.in", "r", stdin);
freopen("virus.out", "w", stdout);
int qaq = 0;
scanf("%d", &qaq);
while(qaq-- > 0) {
scanf("%s", qwq + 1);
n = strlen(qwq + 1);
s[0] = 5;
init();
ln = 1;
for(int i = 1; i <= n; i++) {
s[i] = qwq[i] == 'A' ? 0 : ((qwq[i] == 'T') ? 1 : ((qwq[i] == 'C') ? 2 : 3));
ins(s[i]);
ln++;
}
solve();//dp
}
return 0;
}
C
p是质数也就是存在原根
然后找到一个c,d使得
就转换为了
首先求c,d要BSGS,但是多次询问,我们可以考虑调参实现根号平衡
假设我们要预处理大小为s的,那么有
第一处要特判
此时此时答案为
否则如果P不能整除另一个数无解
或者说直接特判即可
我们想把变成
其中有
但是说其实并不好转换,我们的c,d不一定和m互质啊
首先特判c=d=0,此时等价于C=D的情况,答案为A+B,在特判x=y=1是否可以就能判掉
否则m一定为
然后都除以t后
容易知道
再去设
我们把c,m都除去r,因为把c除以r等价于把cx除以r,所以dy也要除以r
又因为,所以必然有,所以我们考虑把y而不是d拿去除以r
对于答案来说把y除以r,等价于把B乘上r...
再对d也这样做,相当于把A也同等扩大,这样就满足系数和模数互质,就存在逆元了
然后利用扩欧求出d的逆元就能,形式的同余方程
此时处理完c,d可能有或者,此时都是有解的,但是告诉我们有一个不太行,所以可以特判
然后问题变为求
保证,
考虑类欧几里得,定义函数
当x取值在某个区间内是固定的
我们考虑怎么去掉的影响此时
最小值一定在左右端点处
所以最优x要么1. 满足,2. 要么满足
因为注意我们x是n的一倍数所以步长很长
那么对于第一种情况,有
可以知道
k不能为0,否则x=1或者p-1,当x=1或者p-1的时候,我们已经知道答案是什么了
对于
我们总有
但是我们还能再拆一下,观察到p和n的关系,可以写成
于是我们就能类欧下去了
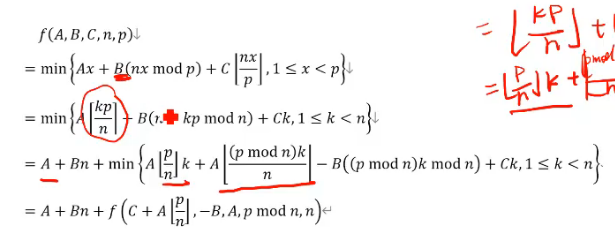
另一种情况是, ,
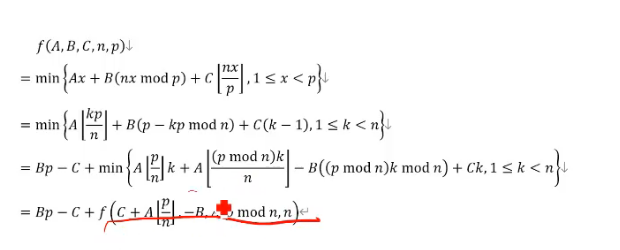
同时因为x=1或者p-1很好求
就是
所以就是
就做完了