某金牌训练营Day4

考虑行列无关,即行的翻转不会影响列的翻折

于是我们求出所有行的方案和列的方案然后直接乘起来即可

就是说,对于只考虑行的一个合法的区间[l,r]他们会贡献 $(r-l+1)*(r-l)/2$ 种选取方案,然后这些方案和任意一个列的选取方案都能凑出一个合法解,说明他是对的

考虑怎么求这两个东西.显然可以区间dp实现

然后我们考虑对于列求合法区间,一个区间合法的充要条件是对于合法区间 $[1,n]$ $[1,l]$ 能够一刀右边,然后 $[r,n]$ 能够移动到左边,这样[l,r]区间一定是合法的

必要性显然,如何证明充分?

首先我们把 $[r+1,n]$ 折过来,第一步显然合法,变为 $[1,r]$

然后剩下部分反证法,假设最靠左的对称轴向右折都跨过右边界,则一定不成立

显然我们可以知道,将整个序列划分成几个部分,然后向右这一段不能跨过n,但是一定跨过r

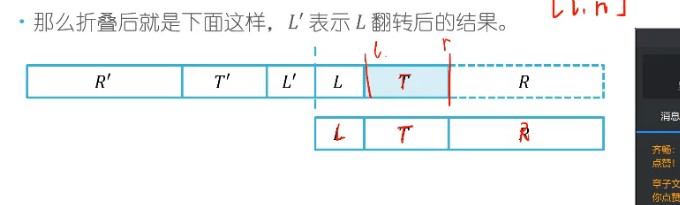
T是原来[l,r],那么我们有,找到R部分最靠左的轴,这个轴翻转过来,是可以把[r+1,n]翻折到[1,r]的

于是我们就能发现,这个轴翻过去就能得到另外一个更靠左的轴,这样的一个轴就能至少保证,翻折过去不会超过R的右端点!

于是我们不断找下去,直到找到这样一条对称轴满足在翻折之后在T右端点之前就是对的

于是我们就证明了充分性

然后我们会发现合法区间的左右端点是独立的,那么我们可以找到所有合法的左右端点,然后前缀和计算出合法区间数即可

比如 $[l,n]$ ,我们要找到合法的这些点

现在的问题在于如何快速找到这些合法的左端点

假设我们现在有合法的左端点x,于是假设他在以i为回文中心的最长回文半径内,我们就可以沿着i翻折一次,然后得到新的左端点

右端点[1,r]也类似

然后前缀和类似的对于一个合法右端点枚举左端点转移即可

要注意实际上并没有单调性这回事...我们是直接找到所有合法的左右端点对....这个东西没有单调性...

维护前i个点的上凸壳,你会发现加入第i个点后,凸壳的导数第二个点就是我们要求的i向左能看到的山峰

然后我们会发现,维护了 $1到i$ 的上凸壳,然后找到i向前的那个点即可,单调栈维护一下

反着重复这个过程我们就知道答案了

然后我们发现每次是看过的最高高度走,那么假设看过的最高高度 $h=y_{to_i}$ ,在h被更新之前是不会改变的

但是说你会发现如果我走到某个点导致i的最高高度目标更新了,那么i之前走路的信息就没用了,相当于等价于从j出发重复这个过程

也就是说我们答案具有可继承性,当历史最大值更新时刻

于是我们如果能够把这棵关系树建出来就能够直接dfs一遍通过继承父亲的答案就做完了

然后我们发现我们要找到的是i向目标走的第一个使i掉头的点,这个点可以二分+区间rmq,也可以使用单调栈,从左向右找解决所有点的向右看的问题,然后从右向左找解决向左看的那些点,每次加入一个点,可能会导致一些点弹出,这些被弹出的点求出他们的 $L,R$ 信息即可,可以用并查集维护吧

如果要在半路上就能掉头呢?

IOI2013的论文有写加强版

我们每次弹出凸壳上点的时候其实就等价于凸包上一条边延长到和这个边有交点了

于是我们把这样的交点额外建立出来即可

然后你会发现每次凸包弹出一个点就会新建立一个点,所以就可以证明复杂度对

#include<bits/stdc++.h>
#define db double
#define ll long long
#define pii pair<int,int>
#define fi first
#define mkp(x,y) (make_pair(x,y))
#define se second
using namespace std;
const int MAXN = 1e6 + 7;
const int MAXLOG = 21;

int n, a[MAXN], b[MAXN], P, c[MAXN];
pii st[MAXN][MAXLOG];
int que[MAXN];
int home[MAXN], nxt[MAXN], to[MAXN], ccnt, len[MAXN], R[MAXN], L[MAXN];

namespace fastIO {
#define BUF_SIZE (1<<21)
	static char buf[BUF_SIZE], *p1 = buf, *pend = buf;
	inline char nc() {
		if(p1 == pend) {
			p1 = buf;
			pend = buf + fread(buf, 1, BUF_SIZE, stdin);
		}
		return *p1++;
	}
	inline int read() {
		int x = 0;
		char s = nc();
		for(; !isdigit(s); s = nc());
		for(; isdigit(s); s = nc())x = (x << 1) + (x << 3) + s - '0';
		return x;
	}
}
using namespace fastIO;

inline void ct(int x, int y, int z) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
	len[ccnt] = z;
}

inline db slope(int x, int y) {
	return (b[y] - b[x]) / (1.0 * a[y] - a[x]);
}

inline void init1() {
	int hd = 1, tl = 0;
	que[++tl] = 1;//一号点没意义
	for(int i = 2; i <= n; ++i) {
		while(hd < tl && slope(que[tl - 1], que[tl]) < slope(que[tl], i))
			--tl;
		L[i] = que[tl];
		que[++tl] = i;
	}
	hd = 1, tl = 0;
	que[++tl] = n;
	for(int i = n - 1; i >= 1; --i) {
		while(hd < tl && slope(que[tl - 1], que[tl]) > slope(que[tl], i))
			--tl;
		R[i] = que[tl];
		que[++tl] = i;
	}
	P = 0;
	for(int i = 1; i <= n; ++i) {
		c[i] = b[L[i]] > b[R[i]] ? L[i] : R[i];
		if(b[P] <= b[i])P = i;
		st[i][0] = max(mkp(b[c[i]], c[i]), mkp(b[i], i));
	}
	return ;
}

inline pii qry(int x, int y) {
	int w = log(y - x + 1) / log(2.0);
	return max(st[x][w], st[y - (1 << w) + 1][w]);
}

inline void init2() {
	for(int j = 1; j <= 20; ++j) {
		for(int i = 1; i <= n; ++i) {
			if(i + (1 << (j - 1)) <= n)//数组越界警告
				st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
		}
	}
	for(int i = 1; i <= n; ++i) {
		if(i == P)continue;
		if(b[R[i]] >= b[L[i]]) {
			int l = i + 1, r = n, mid = 0, ans = R[i];
			while(l <= r) {
				mid = (l + r) >> 1;
				if(qry(i + 1, mid) >= mkp(b[c[i]], c[i])) {
					ans = mid;
					r = mid - 1;
				} else {
					l = mid + 1;
				}
			}
			ct(ans, i, ans - i);
		} else {
			int l = 1, r = i - 1, mid = 0, ans = L[i];
			while(l <= r) {
				mid = (l + r) >> 1;
				if(qry(mid, i - 1) >= mkp(b[c[i]], c[i])) {
					ans = mid;
					l = mid + 1;
				} else {
					r = mid - 1;
				}
			}
			ct(ans, i, i - ans);
		}
	}
	return ;
}

ll ans[MAXN];
inline void dfs(int x) {
	for(int i = home[x]; i; i = nxt[i]) {
		int v = to[i];
		ans[v] = ans[x] + len[i];
		dfs(v);
	}
}

int main() {
	freopen("mountain.in", "r", stdin);
	freopen("mountain.out", "w", stdout);
	n = read();
	for(int i = 1; i <= n; ++i) {
		a[i] = read();
		b[i] = read();
	}
	init1();
	init2();
	dfs(P);
	for(int i = 1; i <= n; ++i)printf("%lld\n", ans[i]);
	return 0;
}

JSOI合金和他一模一样,就是如何快速判断点集都在一条边的一侧比较难

考虑这个点集建立凸包

然后对于一条边(x,y),如果他与凸壳相交,说明我们在凸包的两部分,上凸壳和下凸壳上找到的对应点,满足一个大于等于0,一个小于等于0,就是说叉积结果(汗)

注意我们建立凸包要分上下凸壳维护,然后上下凸壳分界点是横坐标最大和最小的点,二分的时候两个上面都要二分

然后我们可以定义所有顺时针的边(叉积结果大于0)为正向,然后逆时针的边为(叉积结果小于0)反向

然后用floyed求最小环即可!

李队有一个不错的做法,但是被叉了

他认为最优的结构一定是凸壳...

然后就可以使用决策单调性优化建边了,因为这个合法的区域一定是一个双指针的形式

但是说这个显然不对啊,就是我们答案不一定就是凸包啊所以萎了

比如一个凹进去的小三角形就叉了

夏晓光(loveJY)的博客

某金牌训练营Day3