夏晓光(loveJY)的博客

仍要向下扎根,向上结果

首页 归档 标签 关于 友链

某金牌训练营Day8

2021-02-20 20 min read

A

没有强制在线等价于求每一个前缀的答案

然后考虑fail树深度之和怎么做

对于fail树的某个节点i,它对应s的一个前缀s[1:i]s[1:i]

节点i的深度就是i的border的个数

就等价于rightpos个数?

那你就会发现对于任意两个相同的子串,假设为[l1,r1],[l2,r2][l_1,r_1],[l_2,r_2],l1<l2l_1<l_2他的贡献就是所有右端点大于r2r_2,左端点在l1l_1处的所有后缀的贡献

这个贡献数是∣S∣−r2+1|S|-r_2+1,容易发现这个之和r2r_2有关哎,所以我们可以枚举这个后方的子串,然后直接对于后面产生贡献

现在要求的是每一个前缀的g,我们可以差分后变为求端点的贡献,求出这个后前缀和就是答案啦

后缀自动机建立parent树之后,新后缀节点,相当于这个点到根所有节点代表的所有子串都能被表示,因此我们可以一路跳parent树

同时我们可以利用lca的容斥方法,对于之前出现过的,我们把它到根的路径全部加1,然后对于这个节点只需要查询到根的路径和就能得到答案了,需要维护路径带权和,即出现标记总和*代表子串数

这个求出来的就是后缀节点对应的答案


#include<bits/stdc++.h>
#define swap(x,y) (x^=y^=x^=y)
#define ll long long
const int MAXN = 4e5 + 7;//2倍
const int P = 1e9 + 7;
int n;
char s[MAXN];

int ccnt, home[MAXN], nxt[MAXN], to[MAXN], depp, v[MAXN];
inline void ct(int x, int y) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
}

int c[MAXN], ans[MAXN];
namespace sam {
	int fa[MAXN], len[MAXN], ch[MAXN][26], T, lst;
	inline void ins(int c) {
		int p = lst, np = lst = ++T;
		int q, nq;
		len[np] = len[p] + 1;
		for(; p && !ch[p][c]; p = fa[p])ch[p][c] = np;
		if(!p) {
			fa[np] = 1;
			return;
		}
		q = ch[p][c];
		if(len[q] == len[p] + 1) {
			fa[np] = q;
			return ;
		}
		nq = ++T;
		len[nq] = len[p] + 1;
		memcpy(ch[nq], ch[q], sizeof(ch[nq]));
		fa[nq] = fa[q];
		fa[q] = fa[np] = nq;
		for(; ch[p][c] == q; p = fa[p])ch[p][c] = nq;
	}
	inline void ts1() {
		static int qwq[MAXN], qaq[MAXN];
		for(int i = 1; i <= T; ++i)qwq[len[i]]++;
		for(int i = 1; i <= n; ++i)qwq[i] += qwq[i - 1];
		for(int i = 1; i <= T; ++i)qaq[qwq[len[i]]--] = i;
		for(int i = T; i >= 1; --i) {
			int u = qaq[i];
			printf("%d %d %d\n", u, fa[u], len[u]);
		}
		return;
	}
}

int siz[MAXN], son[MAXN], top[MAXN], id[MAXN], dfn[MAXN], dep[MAXN], fa[MAXN]; //好久没写树剖了,一般都LCT的

inline void dfs1(int u, int F) {
	siz[u] = 1;
	fa[u] = F;
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v == F)continue;
		dep[v] = dep[u] + 1;
		dfs1(v, u);
		siz[u] += siz[v];
		if(siz[v] > siz[son[u]])son[u] = v;
	}
	return ;
}

inline void dfs2(int u, int topf) {
	top[u] = topf;
	dfn[++depp] = u;
	v[u] = -sam::len[sam::fa[u]] + sam::len[u];
	id[u] = depp;
	if(!son[u])return ;
	dfs2(son[u], topf);
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v == fa[u] || v == son[u])continue;
		dfs2(v, v);
	}
}

inline int add(int x, int y) {
	x += y;
	if(x >= P)x -= P;
	return x;
}

namespace seg {
#define mid ((l+r)>>1)
	int a[MAXN * 4], b[MAXN * 4], tag[MAXN * 4];
	inline void build(int k, int l, int r) {
		if(l == r) {
			b[k] = v[dfn[l]]; //深度!
			return ;
		}
		build(k << 1, l, mid);
		build(k << 1 | 1, mid + 1, r);
		b[k] = add(b[k << 1], b[k << 1 | 1]); //求和即可
	}
	inline void pushdown(int x) {
		if(tag[x]) {
			tag[x << 1] = add(tag[x << 1], tag[x]);
			tag[x << 1 | 1] = add(tag[x << 1 | 1], tag[x]);
			a[x << 1] = add(a[x << 1], 1ll * tag[x] * b[x << 1] % P);
			a[x << 1 | 1] = add(a[x << 1 | 1], 1ll * tag[x] * b[x << 1 | 1] % P);
			tag[x] = 0;
		}
	}
	inline void mdf(int k, int l, int r, int L, int R, ll w) {
		if(L <= l && r <= R) {
			a[k] = add(a[k], w * b[k] % P);
			tag[k] = add(tag[k], w);
			return ;
		}
		pushdown(k);
		if(L <= mid)mdf(k << 1, l, mid, L, R, w);
		if(R > mid)mdf(k << 1 | 1, mid + 1, r, L, R, w);
		a[k] = add(a[k << 1], a[k << 1 | 1]);
	}
	inline ll qry(int k, int l, int r, int L, int R) {
		if(L <= l && r <= R)return a[k];
		pushdown(k);
		if(R <= mid)return qry(k << 1, l, mid, L, R);
		else if(L > mid)return qry(k << 1 | 1, mid + 1, r, L, R);
		else return add(qry(k << 1, l, mid, L, R), qry(k << 1 | 1, mid + 1, r, L, R));
	}
#undef mid
}

inline void mdfR(int x, int y, int w) {
	while(top[x] != top[y]) {
		if(dep[top[x]] < dep[top[y]])swap(x, y);
		seg::mdf(1, 1, sam::T, id[top[x]], id[x], w);
		x = fa[top[x]];
	}
	if(dep[x] > dep[y])
		swap(x, y);
	seg::mdf(1, 1, sam::T, id[x], id[y], w);
	return ;
}


inline int qryR(int x, int y) {
	int ret = 0;
	while(top[x] != top[y]) {
		if(dep[top[x]] < dep[top[y]])swap(x, y);
		ret = add(ret, seg::qry(1, 1, sam::T, id[top[x]], id[x]));
		x = fa[top[x]];
	}
	if(dep[x] > dep[y])
		swap(x, y);
	ret = add(ret, seg::qry(1, 1, sam::T, id[x], id[y]));
	return ret;
}

inline void init() {
	for(int i = 2; i <= sam::T; ++i)
		ct(sam::fa[i], i);
	dfs1(1, 0);
	dfs2(1, 1);
	seg::build(1, 1, sam::T);//预处理权值和
	return ;
}

inline void solve() {
	for(int i = 1; i <= n; ++i) {
		ans[i] = qryR(1, c[i]);
		mdfR(1, c[i], 1);
	}
	return ;
}

int main() {
	freopen("string.in", "r", stdin);
	freopen("string.out", "w", stdout);
	scanf("%d", &n);
	scanf("%s", s + 1);
	sam::T = sam::lst = 1;
	for(int i = 1; i <= n; ++i) {
		sam::ins(s[i] - 'a');
		c[i] = sam::lst;
	}
	init();//预处理树链剖分
	solve();//预处理答案
	for(int i = 1; i <= n; ++i)ans[i] = add(ans[i], ans[i - 1]);
	for(int i = 1; i <= n; ++i)ans[i] = add(ans[i], ans[i - 1]), printf("%d\n", ans[i]);
	return 0;
}

B

首先只考虑圆弧怎么算吧..

对于长度为i的圆弧,以及他们相对的花,假设他们被两组颜色相同的花包裹在中间

我们考虑这个东西对于答案的贡献,f0(i)f_0(i)也就是说我们只考虑给线段染色的总美丽度

方案数怎么算?

gig_i表示只考虑距离为1,21,2的相同颜色的花的方案数

g0=1,g1=0,gi=gi−2+gi−4g_0=1,g_1=0,g_i=g_{i-2}+g_{i-4}

这个转移就是枚举两个相同颜色的花,他们距离为1的话为i-2,否则为i−4i-4,交叉固定一个

然后我们想要算f0(i)f_0(i)

第一种情况,不存在相对颜色相同的花,总美丽度为gi∗i2g_i*i^2

第二种情况,考虑有一对相对的颜色相同的花跨过去就是划分为了子问题,钦定这个花是第j朵花,此时又会划分为两种情况

  1. 没有一个距离为2花跨过j

我们可以发现此时直接就是两个子问题

gj∗j2∗fi−j−1g_{j}*j^2*f_{i-j-1}

  1. 存在一个距离为2的花跨过j

之前部分的花好像没有什么问题,但是后面的有问题哎

所以我们再次定义f1(i)f_1(i)表示长度为i的,然后开头有一个花搭过来的权值和是什么

此时你发现答案就是gj−1∗j2∗fi−j−2g_{j-1}*j^2*f_{i-j-2}

怎么求f1if_1{i}?

第一种情况,不存在相对颜色相同的花,总美丽度为gi∗(i+1)2g_i*(i+1)^2,注意我们状态的定义是知道有第一个但是不管他

  1. 没有一个距离为2的花跨过j

答案是gj∗(j+1)2fi−j−1g_{j}*(j+1)^2f_{i-j-1}

  1. 存在一个距离为2的花跨过j

此时我们发现其实没什么区别

就是gj−1∗(j+1)2f1i−j−2g_{j-1}*(j+1)^2f_1{i-j-2}

有了这两种情况可以回到环上了

一个破环的技巧是利用相对颜色的花啊

所以我们这里也同样勇一下,钦定第一对相对的花编号为1,n,然后其余的都可以旋转得到

但是我们不知道没有重复的情况下可以旋转几次,也就是说直接就算重了,因此我们可以枚举顺时针第二对相对的花编号为i,那么[2,i−1][2,i-1]不能有相对的花

但是说还是可能有距离为2的花跨过1,i所以我们考虑所有的4中情况只有两端点都被包含没有解决

但是只要类似的将j+1就可以得到递推式子了

然后我们将三个东西观察一下,都可以分治NTT,所以分治NTT一下就好了

具体的写成

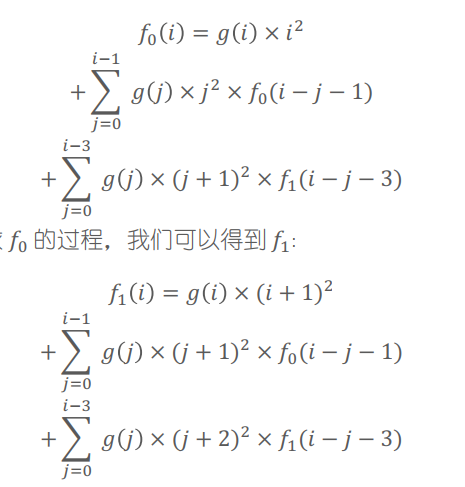
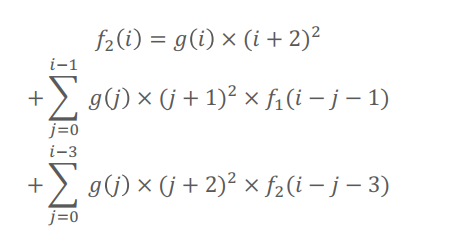
就做完了

本题中如果你BM一下会得到一个十六项的递推公式就能做了

实际上应该是生成函数简单的原因

如果我们将g,F0,F1,f2g,F_0,F_1,f_2都写成生成函数你会发现其实就是相互卷了起来

虽然我们解不出4项变量方程,但是可以知道递推式不会很长

#include<bits/stdc++.h>
using namespace std;
const int P = 998244353;
int n;
int a[] = {0, 4, 8, -1, 16, -10, 4, -12, -48, 26, -44, 15, -16, -4, -4, -1};
int ans[300000];

inline void init() {
	ans[1] = 0;
	ans[2] = 0;
	ans[3] = 24;
	ans[4] = 4;
	ans[5] = 240;
	ans[6] = 204;
	ans[7] = 1316;
	ans[8] = 2988;
	ans[9] = 6720;
	ans[10] = 26200;
	ans[11] = 50248;
	ans[12] = 174280;
	ans[13] = 436904;
	ans[14] = 1140888;
	ans[15] = 3436404;
	ans[16] = 8348748;
	ans[17] = 24631232;
	ans[18] = 64575924;
	return ;
}

inline void add(int &x, int y) {
	x += y;
	if(x >= P)x -= P;
}

int main() {
	freopen("a.in", "r", stdin);
	freopen("a.out", "w", stdout);
	init();
	scanf("%d", &n);
	if(n <= 18)printf("%d\n", ans[n]);
	else {
		for(int i = 19; i <= n; ++i)
			for(int q = 0; q <= 15; ++q) {
				add(ans[i], 1ll * ans[i - q - 1] * a[q] % P);
				ans[i] = (ans[i] + P) % P;
			}
		printf("%d\n", ans[n]);
	}
	return 0;
}

C

取对数

得到直线的形式

yj+aixi>kiy_j+a_ix_i>k_i

注意yi,xi,kiy_i,x_i,k_i都是取ln之后的

我们要找到一个最大的pip_i使得1 pi−11~p_i-1中都没有包含i

这个可以取反,即二分答案,每次询问前t个半平面的交是否包含这个点

因此你会发现我们组成的半平面交一定是一个上凸壳下方的区域,我们可以直接在凸壳上二分找到横坐标范围包含询问点的线段来判断

就是二分找到对应的两点之间,找到直线,然后判断是不是在对应的区域下方就好了

我们求出上凸壳很浪费时间...

发现我们二分的结构是很不错的,我们可以把所有可能的结果维护出来,那么就会发现可以直接O(log2)O(log^2)去回答询问

你会发现对于长度为L的上凸壳,他的复杂度只和区间长度是相关的

那么我们只需要把[l,r][l,r]上建出上凸壳,然后记录这些,然后直接在线回答询问就好了

时间复杂度O(nlog2n)O(nlog^2n),空间O(nlogn)O(nlogn)

这是在线的做法,离线的话可以整体二分

我们可以把所有询问点一起拿出来二分

如果直接整体二分的话,我们再建立[l,r][l,r]的凸壳要排序再去建立凸壳...

否则我们在线时可以归并排序,减少排序的时间

总询问的复杂度显然是O(nlog2n)O(nlog^2n)

怎么用线段建立凸壳?

就是半平面交....

因为如果这个点在所有半平面交处则说明这个点此时不能被表示

递归建立

考虑先把所有直线按照极角排序,从大到小,这个是方向向量和极轴的夹角

然后把所有直线依次插入,对于第i次插入的直线,如果和栈顶直线的交点在栈顶和上一个直线交点的上方,说明我们栈顶就没用了,删掉

否则说明可以直接加入

具体是在上方还是下方和我们维护的凸壳有关,此题维护上凸壳所以可以

具体维护可以看看计算几何初探一文

李队广义凸包

我们可以考虑那些点能成为决策点

因为我们要整体二分所以如果可以判断就能直接做了

考虑所有点按照x坐标排序,然后暴力相当于枚举每一个点a,然后根据他的x再去枚举每一个操作,

xaiy=kx^{a_i}y=k

你会发现随着aia_i增大,那么x越大的点越容易满足条件

然后我们把按照aia_i排序,维护aia_i递减,kk递减的单调栈,栈顶最小

现在我们有x有序的询问,想要判断x什么时候更优,因为要最大化,又有导函数单增,你会发现这个和广义决策单调性是完全一样的,也就是说从栈顶到栈底,最优时间递增,而且满足前者的最优时间一定大于后者,也就是长得像一个

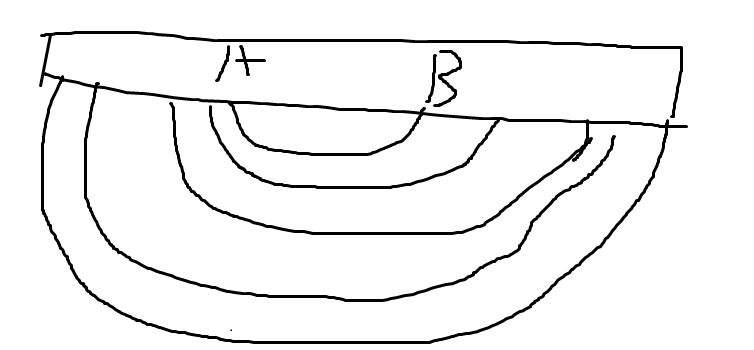
其中一定有B的最优决策点为A,然后每个位置最优决策点是最内层包括他的那个线

所以我们可以二分,或者在本题中直接判交点,找到最优时间,就能维护这个凸壳即可

//半平面交
//考虑建立凸壳的过程是半平面交
//其余是整体二分
//完全可以用李超树代替/xk
//"稍作调逝"
#include<bits/stdc++.h>
using namespace std;
#define db double
const int MAXN = 3e5 + 7;

int n, m;
struct rec {
	db x, y;
	int id;
	rec(db X = 0, db Y = 0): x(X), y(Y) {};
	bool operator<(const rec &p)const {
		return x < p.x;
	}
} a[MAXN], b[MAXN], c[MAXN], d[MAXN];
int ans[MAXN];
int q[MAXN], tl, hd, q1[MAXN], q2[MAXN];

inline rec jd(int x, int y) {
	return rec((c[x].y - c[y].y) / (c[y].x - c[x].x), (c[x].y - c[y].y) / (c[y].x - c[x].x) * c[x].x + c[x].y);
}

inline void solve(int L, int R, int l, int r) {
	if(l == r) {
		for(int i = L; i <= R; ++i)
			ans[a[i].id] = l;
		return ;
	}
	int mid = (l + r) >> 1;
	for(int i = l; i <= mid; ++i)c[i - l + 1] = b[i];
	for(int i = L; i <= R; ++i)d[i - L + 1] = a[i]; //点
	sort(d + 1, d + R - L + 2);
	sort(c + 1, c + mid - l + 2); //极角排序
	//如果这样还小于,就不用活了
	hd = 1, tl = 0;
	for(int i = 1; i <= mid - l + 1; ++i) {
		while(tl > hd && jd(q[tl], i).y <= jd(q[tl - 1], q[tl]).y)--tl;//按照斜率依次加入//对应的cQAQ
		q[++tl] = i;
	}
	int tl1 = 0, tl2 = 0;
	for(int i = 1; i <= R - L + 1; ++i) {
		while(hd < tl && jd(q[hd], q[hd + 1]).x < d[i].x)++hd;//向前扫啊啊啊
		if(d[i].x * c[q[hd]].x + c[q[hd]].y < d[i].y) {
			q2[++tl2] = i;//答案一定大于了
		} else {
			q1[++tl1] = i;//否则向左边吧
		}
	}
	for(int i = 1; i <= tl1; ++i)a[i + L - 1] = d[q1[i]];
	for(int i = 1; i <= tl2; ++i)a[i + L + tl1 - 1] = d[q2[i]];
	if(tl1)solve(L, L + tl1 - 1, l, mid);
	if(tl2)solve(L + tl1, R, mid + 1, r);
	return ;
}

int main() {
	freopen("analysis.in", "r", stdin);
	freopen("analysis.out", "w", stdout);
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; ++i) {
		scanf("%lf%lf", &a[i].x, &a[i].y);
		a[i].x = log(a[i].x);
		a[i].y = -log(a[i].y);
		a[i].id = i;
	}
	for(int i = 1; i <= m; ++i) {
		scanf("%lf%lf", &b[i].y, &b[i].x);//x is k,y is a
		b[i].y = -log(b[i].y);
	}
	b[m + 1].x = -1e16;
	b[m + 1].y = 1; //杀疯了
	solve(1, n, 1, m + 1);
	for(int i = 1; i <= n; ++i)
		if(ans[i] != m + 1)printf("%d\n", ans[i]);
		else puts("-1");
	return 0;
}
Powered by Gridea RSS