RT,只配打网络邀请赛.....

D1T1已经分流了

D1T2 命运

首先考虑容斥,2^m枚举那些限制一定不满足,那么我们其实要解决的就是树上链并这个东西

显然可以每个链记个bitset然后and一下,复杂度是$O(2^mn/w)$24pts

然后我们还有更优一点的做法,就是发现只有链的端点是关键点,然后把那些点拿出来建虚树...

然后会发现虚树上两点之间的边不一定被包括在一个链中,但是还是能做的,比如虚树上差分一下然后再dfs这样子

复杂度$O(2^m*m+nlogn)$实现精细一点可以过40

考虑树上DP,发现可以抛弃容斥的思路了!

重要变成染成黑色

$dp_{i,j}$表示i为根的子树还没确定染色方案,j是最小的满足i的第j个祖先和j+1个祖先之间为黑边的方案数

就是说我们带着父亲已知的染色最近黑边去更新儿子的答案

所以转移方程就是

$dp_{u,j}=\prod_{v\in ch(i)}(dp_{v,j+1}+dp_{v,0})$

分别对应了儿子的边染黑还是不染黑的方案

但是要注意,可能存在点u为下端点的一些限制,使得一些dp状态不合法

优化?要支持区间+,区间清0,单点查询

所以可以线段树合并维护转移.....

$O(nlogn)$

D1T3 时代的眼泪

我...成为了时代的眼泪....

给定一个二维平面，初始给定一个大小为n的点集$(x[i],y[i])$
有m次查询，每次查询有多少点对$(i,j)$，其中$l1<=x[i]<x[j]<=r1$且$l2<=y[i]<y[j]<=r2$

首先有24pts是直接暴力

然后16pts是区间逆序对,可以二次离线莫队

然后12pts是处理出所有逆序对,然后二维数点然后暴力

矩阵之间相互包括?

可以扫描线建树,然后询问就会建成一个森林的形式

之后在森林上启发式合并....这样每个点都只会被加入一次

需要全局用可持久化值域线段树预处理啊....这样才能$O(mlog^2n)$

这个性质直接?四维?莫队是很不错的?

下面写了些这个莫队是可以卡的鬼东西...

100分,第十三分块

数据结构界顶峰

考虑对平面进行分治,然后在此分治结构基础上进行分块

于是对于原点集建立树套树然后这个DAG

共有$log^2n$个节点

考虑怎么维护每个节点的ans?

ans(B)ans(C)ans(D)ans(E)是树套树节点的区间顺序对

本题可以分治的重点在于F与I的贡献是平凡的

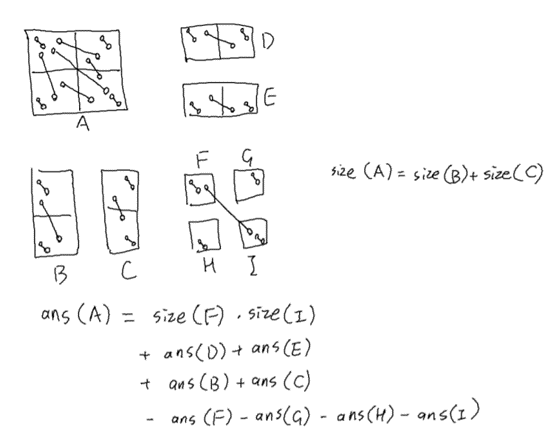
每次查询的时候可以先把$log^2n$树套树节点拿出来然后在上面做类似的容斥

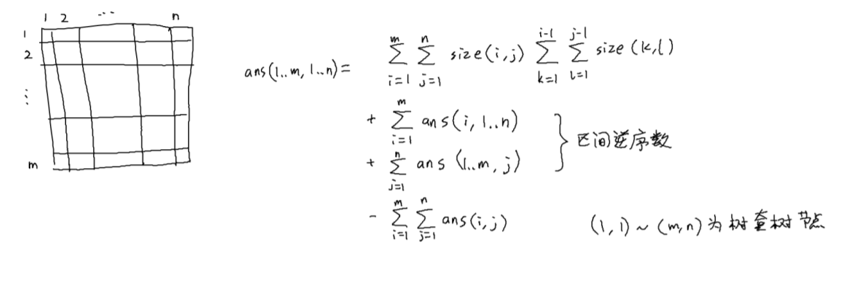
然后我们对于一个平面的分治成功将问题转换成了区间逆序对

询问的不均匀(每层会有看上去log次询问)不会导致答案变差

被删除的nzhtl1477 8:57:14
因为这里的log次询问是分散的，分散到一个指数变化的n上的,每层线段树只访问O(1)个点

这是看不懂的证明

以及Ynoi那道区间逆序对低于$n^{1.5}$的做法

D2T1 制作菜品

考场上瞬间想到了能拼就拼的m>=n-1做法..../xk

然后听完了佳衡的证明感觉茅塞顿开

现在我们的问题其实就是怎么做到n-2

观察大样例的方案不难发现其实就是找出一些数拼起来后能额外再消去一个...

也就是说m=n-1之所以有解是因为我们至少存在一步,能够一下消掉两个数

那么我们就可以猜想m=n-2有解就是至少在最后必消掉两个数之前那一步还存在一步能一下消掉两个数!

所以也就是说,我们能拿一些数凑出k的整数倍

这nm佳衡考场还想了一下?我直接k-转换变成背包啊?

问题变成了能不能找到一些拼起来等于其他某个数

这个显然可以$O(n^2k)$背包输出方案

转移可以用bitset优化!

然后问题就在于bitset优化后怎么输出方案啊

直接记录所有bitset回跳即可QAQ

D2T2 超现实树

三个一缩的想法是错误的,其实给出了卡掉的样例,但是臻大佬没有下载下来于是....

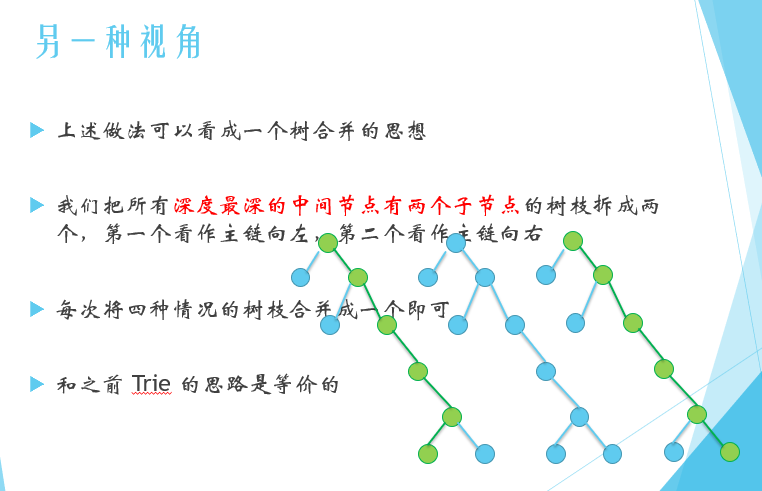
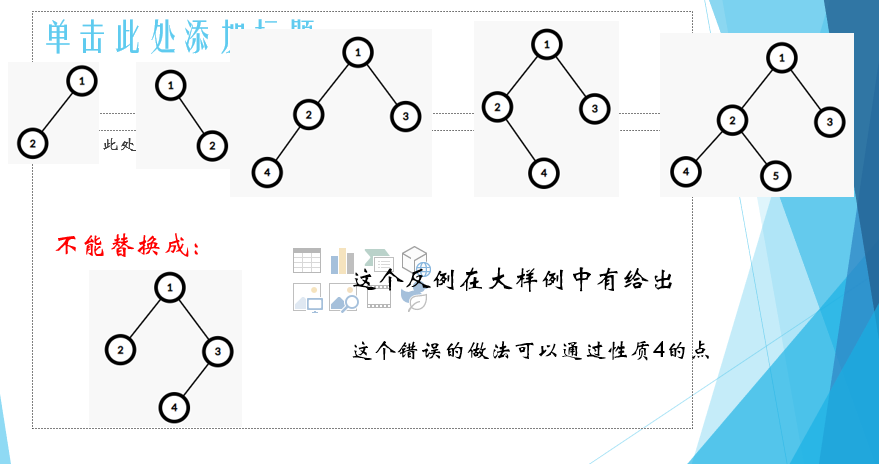
反正我看不懂他在说些什么

#D2T3 翻修道路

最短路有15pts

输出-1有10pts

所以丢了密码条可以25pts

另外B类....好像可以设计可以$f_{i,0/1,0/1}$其实也就是稍稍状压一下

具体细节不会了.....