P1117 [NOI2016]优秀的拆分

NOI2016D1T1

之前提到咕了,所以来补上

先考虑喜闻乐见的95pts算法

我们可以枚举一个中间点,计算一下他向前能形成的AA总串数,向后能形成的BB串的总串数

ans=\sum_{i=1}^n{a[i]*b[i]}

这个 $n^2$

然后再考虑5pts做法(

我们考虑枚举一个len,然后计算每个点是否是一个长度为2len的AA串的开头

那我们每个len放一个tag,这样每个2*len的串都至少经过2个tag

我们想,好像要快一点就只能求个LCS或LCP快一点了......

那么我们对相邻两个tag求个前缀的LCS,而后缀求一个LCP,得到下图

蓝是LCS,绿是LCP

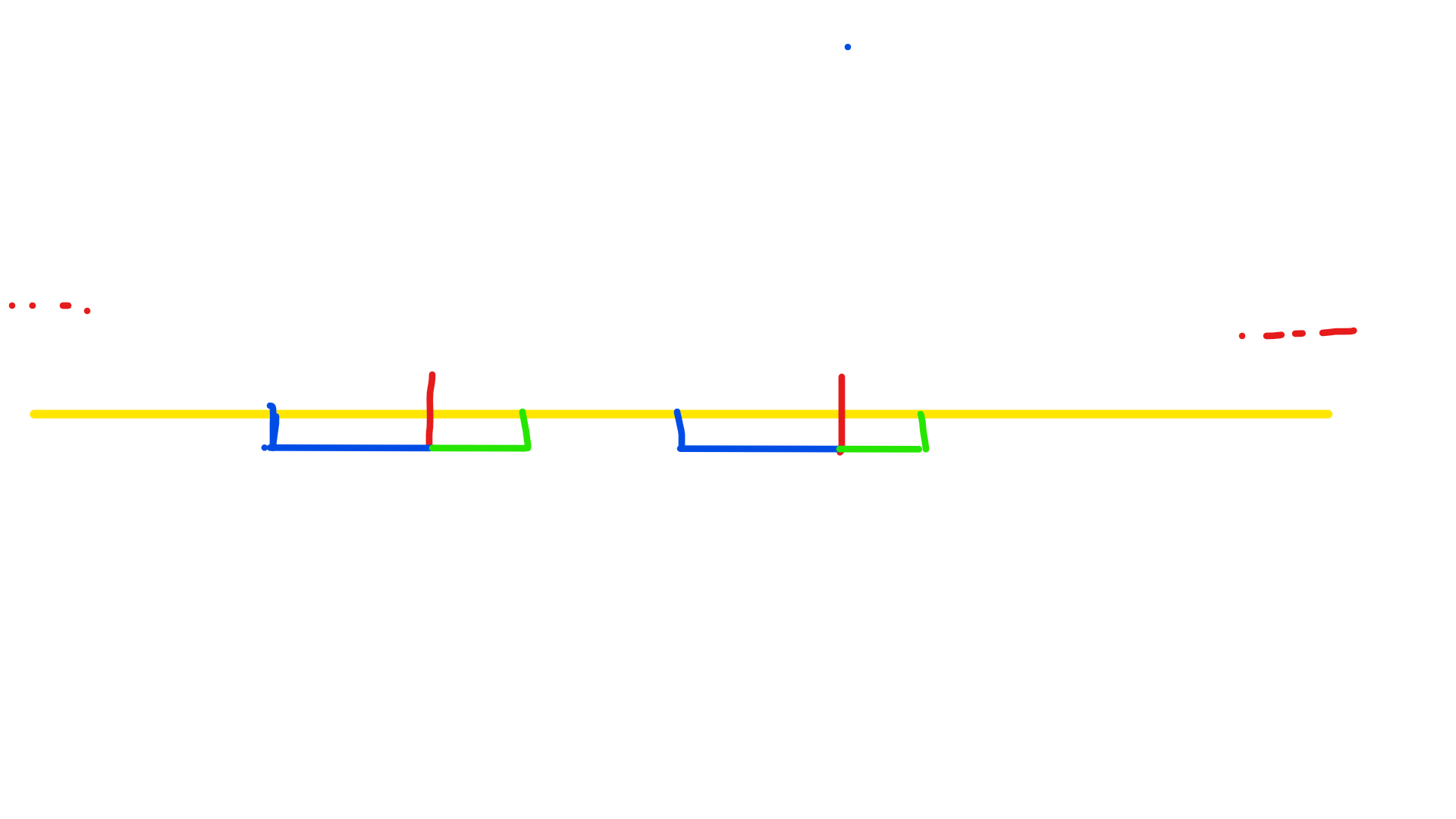
此时一定没有一个长度为2*len的AA串经过,因为这最大相等两段根本不连续,其中长度为A的一段和下一段一定有一个位置不同

再考虑如果这个长度足够长呢?

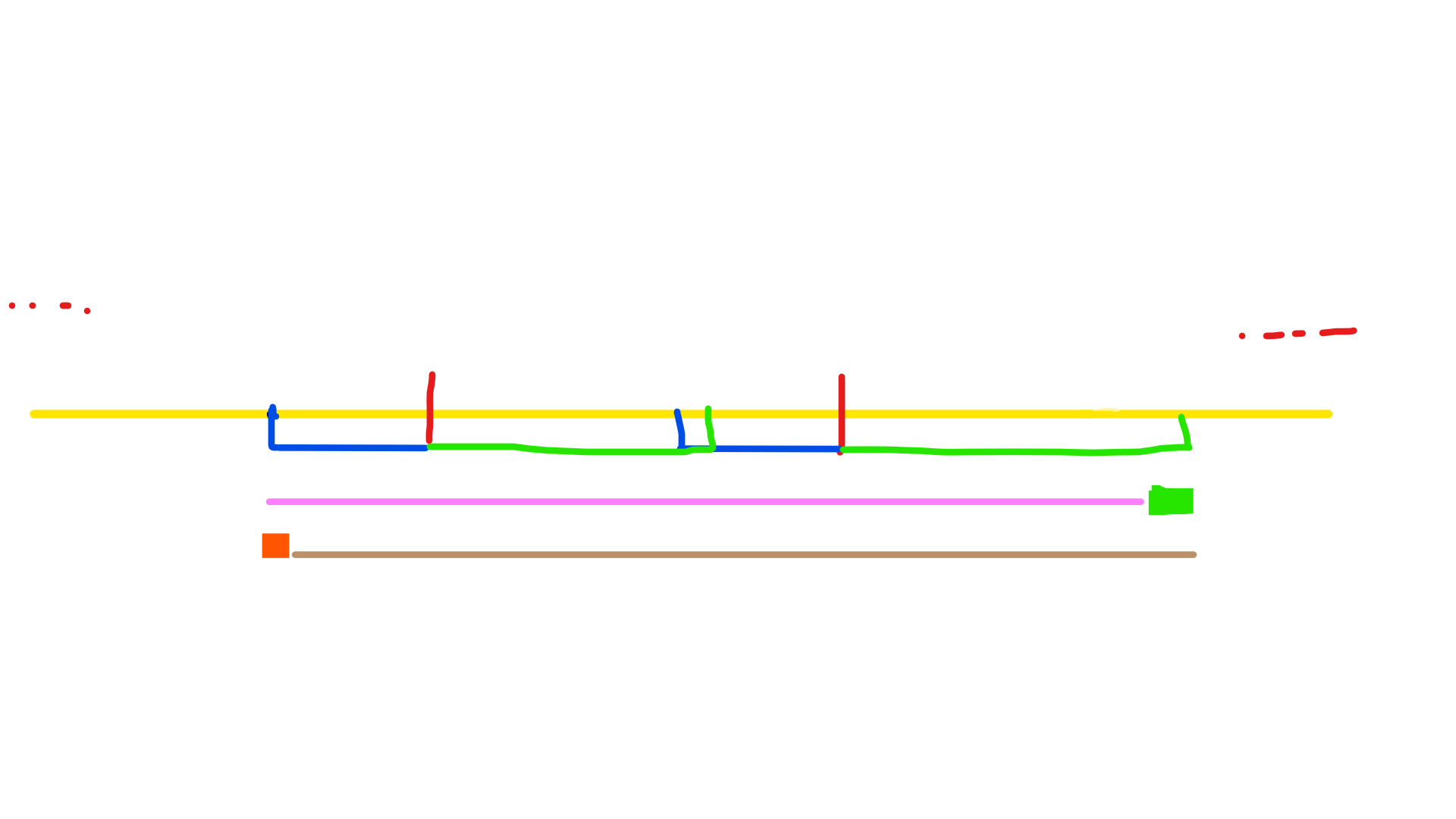
那么粉色开头到红色结尾一段都可以作为起始点,而绿色一段中都可以作为结尾点

这个就是一个差分的标记了,最后统计答案就行了

code:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#define ll long long
using namespace std;
const int MAXN=6e4+3;
int n;
string s;
int res1[MAXN],res2[MAXN];

struct SAM {
	int c[MAXN],sa[MAXN],fa[MAXN],len[MAXN],tag[MAXN];
	int f[MAXN],son[MAXN],top[MAXN],siz[MAXN],dep[MAXN];
	int cnt,lst;
	map<char,int> ch[MAXN];
	struct edge {
		int to,nxt;
	} e[MAXN<<1];
	struct Gr {
		int ccnt,home[MAXN];
		struct edge {
			int to,nxt;
		} e[MAXN<<1];
		inline void add(int u,int v) {
			e[++ccnt]= {v,home[u]},home[u]=ccnt;
			e[++ccnt]= {u,home[v]},home[v]=ccnt;
		};
	} G;
	inline void ins(char c,int id) {
		int p=lst;
		int np=++cnt;
		//	printf("%d?%d\n",p,np);
		lst=np,tag[id]=np,len[np]=len[p]+1;
		for(; p&&!ch[p][c]; p=fa[p])ch[p][c]=np;
		if(!p)fa[np]=1;
		else {
			int q=ch[p][c];
			if(len[q]==len[p]+1)fa[np]=q;
			else {
				int nq=++cnt;
				len[nq]=len[p]+1,ch[nq]=ch[q];
				fa[nq]=fa[q],fa[q]=fa[np]=nq;
				for(; p&&ch[p][c]==q; p=fa[p]) ch[p][c]=nq;
			}
		}
	}
	void dfs(int u,int fa) {
		siz[u]=1;
		//printf("%d?%d\n",u,fa);
		for(int i=G.home[u]; i; i=G.e[i].nxt) {
			int v=G.e[i].to;
			if(v!=fa) {
				dep[v]=dep[u]+1;
				f[v]=u;
				dfs(v,u);
				siz[u]+=siz[v];
				son[u]=siz[v]>siz[son[u]]?v:son[u];
			}
		}
	}
	void dfs(int u) {
		if(!top[u])top[u]=u;
		if(son[u])top[son[u]]=top[u],dfs(son[u]);
		for(int i=G.home[u]; i; i=G.e[i].nxt) {
			int v=G.e[i].to;
			if(v^f[u]&&v^son[u])dfs(v);
		}
	}
	inline void init() {
		for(int i=1; i<=cnt; ++i)f[i]=fa[i],G.add(f[i],i);//fail
		dfs(1,0),dfs(1);
	}
	inline int query(int u,int v) {
		u=tag[u],v=tag[v];
		for(; top[u]^top[v]; u=f[top[u]]) {
			if(dep[top[u]]<dep[top[v]])swap(u,v);
		}
		return len[dep[u]<dep[v]?u:v];
	}
} samp,saml,zero;

inline int Min(int a,int b) {
	return a<b?a:b;
}

int main() {
	//freopen("test.in","r",stdin);
	//ios::sync_with_stdio(false);
//	puts("qwq");
	int T;
	cin>>T;
//	cout<<T<<'\n';
	zero.cnt=zero.lst=1;
	while(T-->0) {
		s.clear(),cin>>s,n=s.length();
		memset(res1,0,n+3<<3);
		memset(res2,0,n+3<<3);
		samp=zero,saml=zero;
		//puts("233");
		for(int i=0; i<=n-1; ++i)samp.ins(s[i],i+1);
		//	puts("233");
		for(int i=n-1; i>=0; --i)saml.ins(s[i],i+1);//建反串
		samp.init(),saml.init();
		for(int len=1; len<=(n>>1); ++len) {
			for(int i=len; i+len-1<=n; i+=len) {
				int j=i+len,hm=0,qm=0;
				if(j<=n)hm=Min(saml.query(i,j),len);
				if(i>1)qm=Min(samp.query(i-1,j-1),len-1);
				if(qm+hm<len)continue;
				--res1[j+hm],++res1[j+hm-1-(qm+hm-len)];
				++res2[i-qm],--res2[i-qm+1+(qm+hm-len)];
                //对于结尾和开头分别差分
			}
		}
		for(int i=1; i<=n; ++i)res1[i]+=res1[i-1],res2[i]+=res2[i-1];
        //求前缀和
		ll ans=0;
		for(int i=2; i<=n; ++i)ans+=1ll*res1[i-1]*res2[i];
		printf("%lld \n",ans);
	}
	return 0;
}

夏晓光(loveJY)的博客

P1721 [NOI2016]国王饮水记