P1232 [NOI2013]树的计数

NOI2013DxTx

不能再咕了,这个确实是思维好题呢,真实原因是真正的鸽子是有补救的时候的

好了我在说什么啊这个开头已经越来越水了

给出一个DFS序和一个BFS序求所有满足这两个序的树的平均深度(其实就是期望)
$100%$ , $2 \le n \le 2 \times 10^5$ 。

看完题直接完蛋,我想起NOIP的染色游戏,从题解找思路!

我们发现这个答案好像和BFS的段数有关啊....因为BFS每次多一段,树的深度就+1

而把BFS随手分段算答案显然是不满足DFS序的QAQ

那么考虑BFS序每个位置能不能分段,分三种情况

必须分 1
必须不能分 0
可分可不分 0.5

设节点i的dfs中出现位置是dfn[i],同理bfn[i]

那么我们让i=bfn[i],id[i]=实际i,也就是说我们按照bfs序重新编号

那么按照bfs序连续的两个点y,x,满足y=x+1

然后dfn[y]< dfn[x]你会发现我们一定要分新的一层

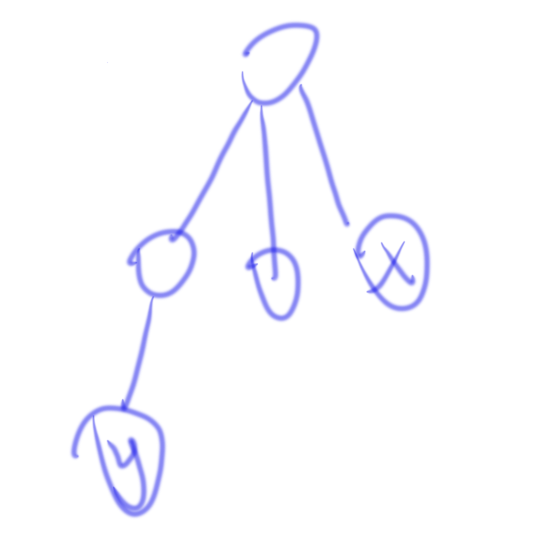
否则我们一定满足bfs序y< x

有了这个结论,我们不难发现如果dfn[x+1]<dfn[x],就一定有1的贡献

这个条件还不够如果dfn[x+1]>dfn[x]呢?你会发现我们确定不了x+1和x的相对位置也就是说贡献是0.5

如果dfs序连续呢?x,y的dfs序连续

x>y-1 注意这里是bfs的大于啊说明y是x某个祖先的儿子,这个好像并不影响分层,也就说没啥用
x==y-1 也就是说y作为x的兄弟还是儿子都是合法的,因为此时xy的dfs序也是连续的,一个是0一个是1

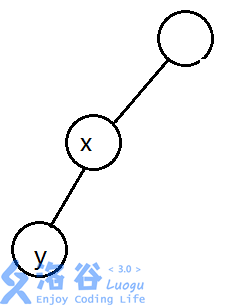
所以还是没有任何影响/摊手

x< y-1,此时y是x的儿子,这种情况好玩,我们画个图

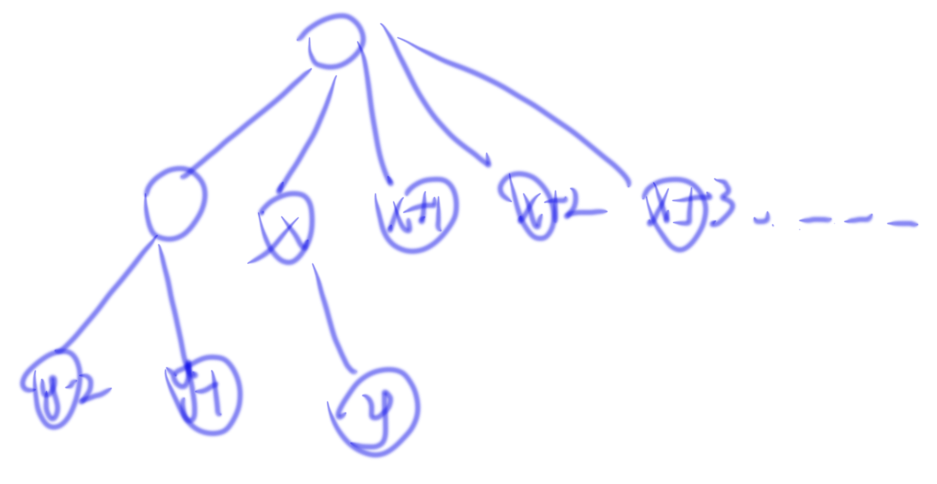
然后你会发现其中一定有且只有一个位置他的贡献是1,其他的贡献都是0!

这个也就是说我们[x,y)区间没有贡献

其他位置...看来只能贡献0.5了

然后最后这些限制显然必要,但是我们并不能证明他们是否充分啊QAQ

因为这完全可以通过这道神仙题.....

code:


#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline int read() {
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9') {
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return x*f;
}
const int N=2e6+7;
int n;
double ans;
int dfn[N],pos[N],sum[N];//sum是差分数组
//dfn是节点的dfs序，pos是dfn的反数组，所以有 pos[dfn[i]]=i,dfn[pos[i]]=i
inline void mark(int x,int y) {
	sum[x]++,sum[y+1]--;    //打差分标记
}
int main() {
	// freopen("1.in","r",stdin);
	n=read();
	ans=1;
	mark(1,1);//第一个节点一定要分一层
	for(int i=1; i<=n; i++) dfn[read()]=i; //读入初始dfs序
	for(int i=1; i<=n; i++) pos[dfn[read()]]=i; //用初始dfs序更新变化后的pos
	//上面一行不太好想。因为bfs序重标号了，原来的节点read()就变成了i，所以pos[dfn[read()]]=i
	for(int i=1; i<=n; i++) dfn[pos[i]]=i; //用更新后的pos更新dfn
	for(int i=1; i<n; i++) { //注意i不取n
		if(dfn[i]>dfn[i+1]) ans++,mark(i,i);//注意这里也要打标记，之后不会再产生0.5的贡献
		if(pos[i]<pos[i+1]-1) mark(pos[i],pos[i+1]-1);//打标记
	}
	int now=0;
	for(int i=1; i<n; i++) now+=sum[i],ans+=(now ? 0 : 0.5); //如果这个位置不确定则贡献为0.5
	//注意上一行i不取n,因为切的位置只有n-1个
	ans+=1;//深度等于分的段数+1
	// printf("%.3lf\n%.3lf\n%.3lf",ans-0.001,ans,ans+0.001);//BZOJ上要这样输出...
	printf("%.3lf\n",ans);
	return 0;
}

所以我们可以把它改改毒瘤他人?

夏晓光(loveJY)的博客

P5289 [十二省联考2019]皮配