P1399 [NOI2013]快餐店

NOI系列

上午颓了1.5h自闭了.....TAT

点开题随便看看感觉是求树的直径然后输出中间点,这个和之前那个集训队作业很像~~集训队作业nb~~

然后仔细一看是基环树/惊恐

基环树直径怎么求呢?

找出那个环,这里有个很妙的方法,就是根据dfn大小关系和fa数组横跳就可以得到整个环,具体看代码
环上的点所在的树以环上点为根,求一个内部直径更新答案,同时得到最长链
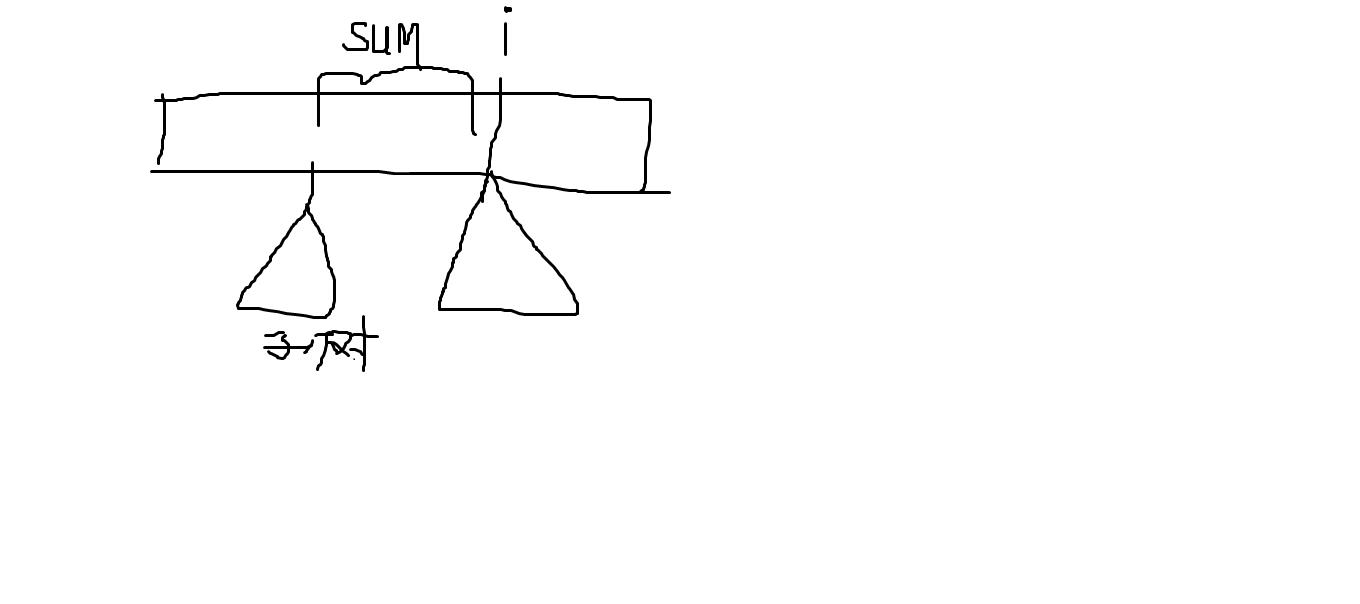
求一遍前缀sum+最长链长度最大值,即图1,同时求一下从前面某个点到i这段构成直径的最大值,即图2
把3从求前缀变为求后缀
枚举每个位置进行组合

没有了

图1:

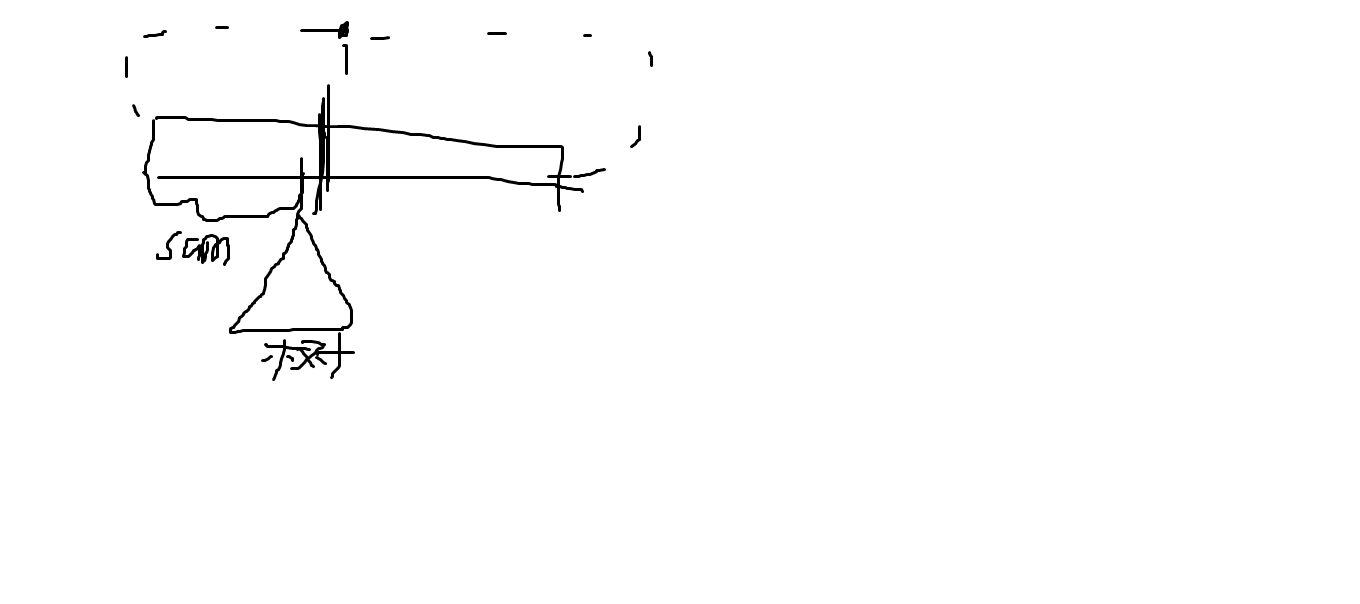
图2:

code:


#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#include<map>
using namespace std;
#define ll long long
const int MAXN=2e5+7;
const int inf=0x3f3f3f3f;
const int P=1e9+7;
int n;
struct rec {
	int to,nxt,w;
} edge[MAXN<<1];
int home[MAXN<<1],ccnt=0;
int huan[MAXN],huan_cnt=0,huan_zhi[MAXN],cost[MAXN],fa[MAXN],huan_sign[MAXN];
int dfn[MAXN],timee=0;
ll dis[MAXN];
ll ans=0,ans1=0;
ll A[MAXN],B[MAXN];
ll C[MAXN],D[MAXN];

namespace fastIO {
#define BUF_SIZE (1<<19)
	static char buf[BUF_SIZE],*p1=buf+BUF_SIZE,*pend=buf+BUF_SIZE;
	inline char nc() {
		if(p1==pend) {
			pend=buf+fread(buf,1,BUF_SIZE,stdin);
			p1=buf;
		}
		return *p1++;
	}
	inline int read() {
		int x=0,f=1;
		register char s=nc();
		for(; !isdigit(s); s=nc())if(s=='-')f=-1;
		for(; isdigit(s); s=nc())x=(x<<1)+(x<<3)+s-'0';
		return x*f;
	}
}
using namespace fastIO;

inline void add(int x,int y,int z) {
	edge[++ccnt].to=y;
	edge[ccnt].w=z;
	edge[ccnt].nxt=home[x];
	home[x]=ccnt;
}

inline void input() {
//	freopen("test.in","r",stdin);
	int xx,yy,zz;
	n=read();
	for(int i=1; i<=n; ++i) {
		fa[i]=i;
		xx=read();
		yy=read();
		zz=read();
	//	printf("%d %d %d\n",xx,yy,zz);
		add(xx,yy,zz);
		add(yy,xx,zz);
	}
}

inline void dfs(int u) {
	dfn[u]=++timee;
//	printf("%d:\n",u);
	for(int i=home[u]; i; i=edge[i].nxt) {
		int v=edge[i].to;
		if(v!=fa[u]) {
			if(!dfn[v]) {
			//	printf("%d %d !\n",u,v);
				fa[v]=u;
				cost[v]=edge[i].w;
				dfs(v);
			} else if(dfn[v]>dfn[u]) {
			//	printf("%d %d?\n",u,v);
			//	printf("%d %d???\n",u,v);
				for(; v!=u; v=fa[v])
				{
				//	printf("%d %d????\n",u,v);
					huan_sign[v]=1;
					huan[++huan_cnt]=v;
					huan_zhi[huan_cnt]=cost[v];
				}
				huan_sign[u]=1;
				huan[++huan_cnt]=u;
				huan_zhi[huan_cnt]=edge[i].w;
			}
		}
	}
	//找环并统计环上边权
}

inline void DP(int u,int FA) {
	for(int i=home[u]; i; i=edge[i].nxt) {
		int v=edge[i].to;
		if(!huan_sign[v]&&v!=FA) {
			DP(v,u);
			ans=max(1ll*dis[u]+dis[v]+edge[i].w,ans);
			// 第一类答案
			dis[u]=max(dis[u],dis[v]+edge[i].w);
		}
	}//树形dp ,求出环上子树的最长链
}

inline void solve() {
	dfs(1);
	for(int i=1; i<=huan_cnt; ++i)
		DP(huan[i],0);
	//先dpqwq
//	for(int i=1; i<=huan_cnt; ++i)printf("%d??\n",huan[i]);
	ll sum=0,maxx=0;
	for(int i=1; i<=huan_cnt; ++i) {
		sum+=huan_zhi[i-1];//sum是前缀环权和
		A[i]=max(A[i-1],dis[huan[i]]+sum);//A[i]是从环上1号点->i最长的qwq
		B[i]=max(B[i-1],sum+maxx+dis[huan[i]]);//B[i]是从之前的某点出发到i的最大 (不绕环
		maxx=max(maxx,dis[huan[i]]-sum);
	}
	sum=maxx=0;
	int tmp=huan_zhi[huan_cnt];
	huan_zhi[huan_cnt]=0;

	for(int i=huan_cnt; i>=1; --i) {
		sum+=huan_zhi[i];
		C[i]=max(C[i+1],dis[huan[i]]+sum);
		//前驱从1->sth最大的
		D[i]=max(D[i+1],sum+maxx+dis[huan[i]]);
		maxx=max(maxx,dis[huan[i]]-sum);
		//这里从后到前再考虑后缀,从i到后面
	}
	ll tep;
	ans1=B[huan_cnt];
	for(int i=1; i<huan_cnt; ++i) {
		tep=max(B[i],D[i+1]);//要么只考虑i左端点

		tep=max(tep,A[i]+C[i+1]+tmp);//要么从i到前一段+从i到后一段绕过整个环
		ans1=min(ans1,tep);
	}
	ans=max(ans,ans1);
	if(ans&1)printf("%lld.5\n",ans>>1);
	else printf("%lld.0\n",ans>>1);
}

int main() {
	input();
	solve();
	return 0;
}

夏晓光(loveJY)的博客

CF504E Misha and LCP on Tree