夏晓光(loveJY)的博客

九省联考D1T1

哇偶,状压DP我果然还是不会的,要多做些才行呢

如果考场考了是不是就TAT了啊

简要题意没有了

上去直接考虑n=2m=2,发现可以手算所有决策

以及还有n=10m=1,会发现我们只能从左到右放

然后没了,正解吧

轮廓线DP

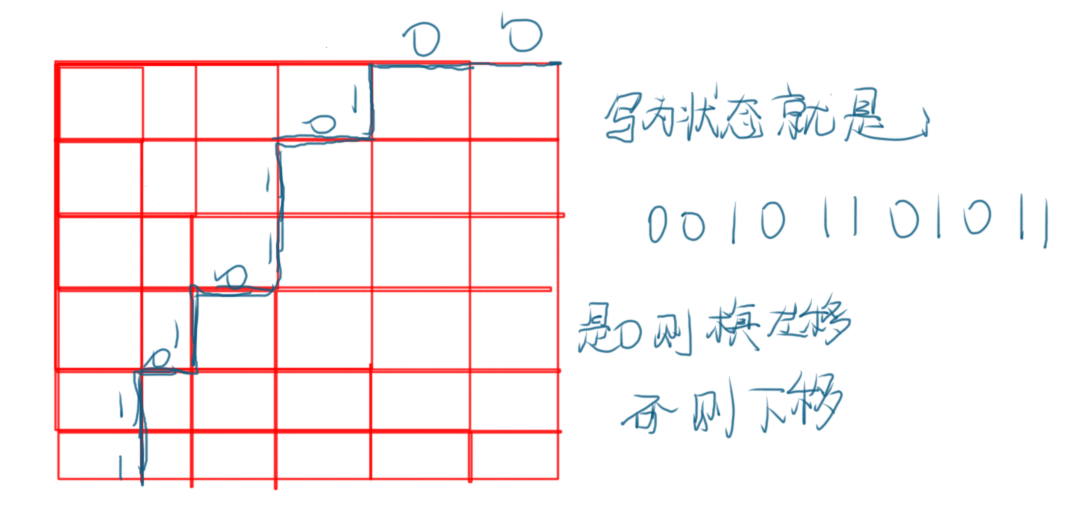
一种挺奇妙的DP状态设计方式啊!

我们把n+m-1个行和列压起来,然后这一位为0表示轮廓线是横着的边,如果为1就表示轮廓线为竖着的边

被轮廓线围住的三角形就是放棋子的格子

然后你会发现这个状态的设计很不错,因为他充分利用了每个信息------这个棋盘一定满足放置是一个从右上到左下的三角形

而且我们可以通过0/1来定位棋子具体在哪一个格子,从而实现转移qwq

eg:

code:

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

namespace fastIO {
#define BUF_SIZE (1<<19)
	static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = buf + BUF_SIZE;
	inline char nc() {
		if(p1 == pend) {
			p1 = buf;
			pend = buf + fread(buf, 1, BUF_SIZE, stdin);
		}
		return *p1++;
	}
	inline int read() {
		int x = 0, f = 1;
		register char s = nc();
		for(; !isdigit(s); s = nc())if(s == '-')f = -1;
		for(; isdigit(s); s = nc())x = (x << 1) + (x << 3) + s - '0';
		return x * f;
	}
}
using namespace fastIO;
const int MAXN = 10;
const int P = 1e9 + 7;

int a[MAXN][MAXN], b[MAXN][MAXN];

int f[1 << (MAXN << 1)];

int dfs(int sta, bool who, int n, int m) {
	if(~f[sta])return f[sta];
	f[sta] = who ? -P : P;
	int x = n, y = 0;
	for(int i = 0; i < n + m - 1; ++i) {
		if(sta >> i & 1)x--;
		else y++;
		if((sta >> i & 3) != 1)
			continue;
		int nxt = sta ^ (3 << i);
		if(who)
			f[sta] = max(f[sta], dfs(nxt, who ^ 1, n, m) + a[x][y]);
		else
			f[sta] = min(f[sta], dfs(nxt, who ^ 1, n, m) - b[x][y]);
	}
	return f[sta];
}


int main() {
	// freopen("test.in", "r", stdin);
	int n = read(), m = read();
	for(int i = 0; i < n; ++i) {
		for(int j = 0; j < m; ++j) {
			a[i][j] = read();
		}
	}
	for(int i = 0; i < n; ++i) {
		for(int j = 0; j < m; ++j) {
			b[i][j] = read();
		}
	}
	memset(f, -1, sizeof(f));
	f[((1 << n) - 1) << m] = 0;
	printf("%d\n", dfs((1 << n) - 1, 1, n, m));
}

$Orzljh$