P4364 [九省联考2018]IIIDX

九省联考D1T2

吐槽这样的弱者只会弄水题

另外![](/.......)....本来这里应该有张p站的图的

给你一颗树和一些权值,要求你给这个树分权值,满足父亲的权值小于儿子而且按照bfs序越靠前的点权值越大,输出方案

$n<=1e5$

首先我们有个一眼的做法就是考虑直接贪心,就是给编号最小的儿子最大的siz个去组方案

先把权值按照从大到小排序能快一点

然而如果出现权值相等的情况就命没了,eg 4 2.0 1 1 2 1

你会这样划分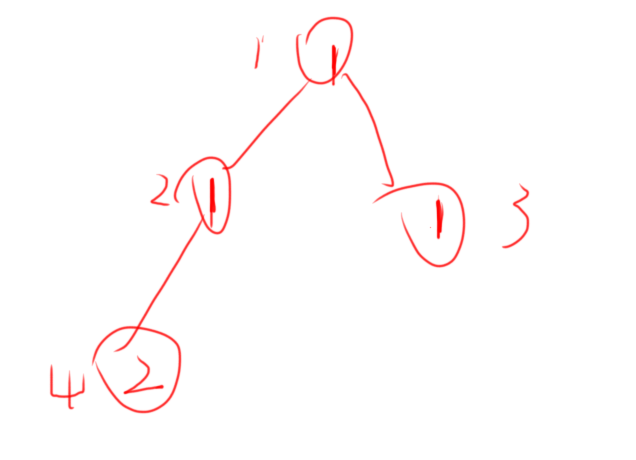

然后命没了

所以我们要改改这个做法

为什么不对?因为我们是按照dfs序去划分,而题面中都提示你按照bfs序去做了

所以我们再想直接按照bfs序去做要怎么搞

也就是说我们要同时维护父亲预留大小和查询这个点的最大可能性

线段树

1.维护前缀有多少个点可以选

没了

然后你会发现一个之前贪心不用搞的事情,就是我们相等的权值一定要尽可能右边的,因为线段树上相等的一列按照这个方法做是右边更优左边更劣的...当然这是在同一层的视角下

update:将完课后被神仙队友爆锤,一堆锅....还现场模拟代码/xk/xk/xk

你会发现我们可能会出现选完一个点预留好了然后又去选了左边使得预留不够吗?

不可能,因为我们二分只看右边啊

你会发现如果我们出现一个点为0的情况而我们二分到了这个点吗?

此时看代码会自动+1,这个+1也是为了处理这个而来的

消极.

谁知道呢?

code:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
const int MAXN = 5e5 + 7;
const int inf = 1e9;
using namespace std;
struct rec {
    int mn, del;
} tr[MAXN << 2];
int n, N;
double k;
int a[MAXN], b[MAXN], ans[MAXN], siz[MAXN], fa[MAXN], cnt[MAXN];

namespace fastIO {
#define BUF_SIZE (1<<19)
    static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = buf + BUF_SIZE;
    inline char nc() {
        if(p1 == pend) {
            p1 = buf;
            pend = buf + fread(buf, 1, BUF_SIZE, stdin);
        }
        return *p1++;
    }
    inline int read() {
        int x = 0, f = 1;
        char s = nc();
        for(; !isdigit(s); s = nc())if(s == '-')f = -1;
        for(; isdigit(s); s = nc())x = (x << 1) + (x << 3) + s - '0';
        return x * f;
    }
}
using namespace fastIO;

inline bool cmp(int a, int b) {
    return a > b;
}

inline void add(int x, int delta) {
    tr[x].del += delta;
    tr[x].mn += delta;
}

inline void up(int x) {
    tr[x].mn = min(tr[x << 1].mn, tr[x << 1 | 1].mn);
}

inline void down(int x) {
    add(x << 1, tr[x].del);
    add(x << 1 | 1, tr[x].del);
    tr[x].del = 0;
}

inline void build(int k, int l, int r) {
    if(l == r) {
        tr[k].mn = l;
        return ;
    }
    int mid = (l + r) >> 1;
    build(k << 1, l, mid);
    build(k << 1 | 1, mid + 1, r);
    up(k);
}

inline int query(int k, int l, int r, int qwq) {
    if(l == r) {
        return (tr[k].mn >= qwq ? l : l + 1);
    }
    down(k);
    int mid = (l + r) >> 1;
    if(qwq <= tr[k << 1 | 1].mn)return query(k << 1, l, mid, qwq);
    else return query(k << 1 | 1, mid + 1, r, qwq);
}

inline void update(int k, int l, int r, int L, int R, int D) {
    if(L <= l && R >= r) {
        tr[k].mn += D;
        tr[k].del += D;
        return ;
    }
    down(k);
    int mid = (l + r) >> 1;
    if(L <= mid)update(k << 1, l, mid, L, R, D);
    if(R > mid)update(k << 1 | 1, mid + 1, r, L, R, D);
    up(k);
}

int main() {
    // freopen("test.in", "r", stdin);
    scanf("%d", &n);
    scanf("%lf", &k);
    for(int i = 1; i <= n; ++i)a[i] = read();// printf("%d?\n", a[i]);
    sort(a + 1, a + n + 1, cmp);
    for(int i = n - 1; i; i--) {
        // printf("%d %d\n", a[i], a[i + 1]);
        if(a[i] == a[i + 1])cnt[i] = cnt[i + 1] + 1;
        else cnt[i] = 0;
    }
    for(int i = 1; i <= n; ++i) {
        fa[i] = (int)floor(i / k);
        // printf("%d \n", fa[i]);
        siz[i] = 1;
    }
    for(int i = n; i; --i) {
        siz[fa[i]] += siz[i];
        // printf("%d?\n ", siz[i]);
        //统计子树和
        //SAM基操
    }
    build(1, 1, n);
    for(int i = 1; i <= n; ++i) {
        // printf("%d %d?\n", fa[i], siz[fa[i]] - 1);
        if(fa[i] && fa[i] != fa[i - 1])
            update(1, 1, n, ans[fa[i]], n, siz[fa[i]] - 1);
        int x = query(1, 1, n, siz[i]);
        // printf("%d %d\n", x, cnt[x]);

        x += cnt[x];
        // printf("%d ?", x);
        cnt[x]++;
        // printf("%d \n", cnt[x]);

        ans[i] = x;
        update(1, 1, n, x, n, -siz[i]);
    }
    for(int i = 1; i <= n; ++i)printf("%d ", a[ans[i]]);
    return 0;
}

Orzhq

夏晓光(loveJY)的博客

P6381 『MdOI R2』Odyssey