P5284 [十二省联考2019]字符串问题

十二省联考D1T2

没啥感想,就是10s时限确实毒瘤

给出一个母串 $S$ 。

有一些 $A$ 类串和一些 $B$ 类串，都是 $S$ 的子串，以左右端点的方式给出。

给出一些 $A$ 类串对 $B$ 类串的支配关系。

我们需要用若干个 $A$ 类串首位顺次相连，要求对于每相邻两个 $A$ 类串，必须存在一个 $B$ 类串被前一个串支配，且是后一个串前缀。我们想让连接后的串尽量长，输出这个长度。如果可以无限长，输出"-1"。

首先这是省选,而且考字符串,所以盲猜要后缀数据结构

用脑子想想暴力做法就是枚举两个点然后判断能不能连边....接着跑一个拓扑排序求最长链,如果有环就是-1

问题是直接这样做什么都过不了,复杂度 $O(n^2*m)$ 我们考虑建图时间浪费在哪里

判断两个点是否是可以做前后相接的关系,就是A是不是B所支配的某个点的一个扩集
枚举两个点这个过程本身,也就是连边太慢了

所以我们先建立反串的SAM,为什么不是SA?因为我不会为什么是反串?因为我们需要后缀树,这样他的超集就在子树和本节点比他长的串上了

然后我们边分两种

从A连向被支配的B,A的权值是长度,B的权值是0
从B指向以他为前缀的A

我们发现难度主要在2号点,不过想想后缀树其实也并不难

首先要用倍增的方式得到子串在原树上的位置,就是子串开头节点是谁,记录在结尾节点上

然后,我们这样的方式连边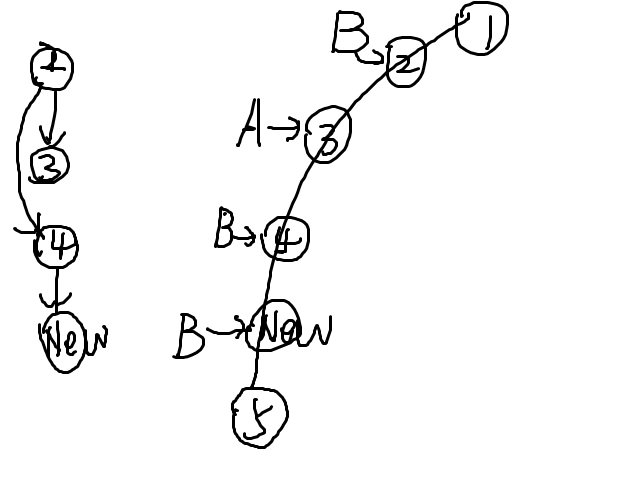

也就是说,我们在五号点把接收到的上方节点先按照长度从小到大排序,再B串前A串后,然后每个串都由他最近的B连向他!!

最后每个结尾点都记录了离得最近的一个B点,我们再用后缀树的树边,把这个b点向他的儿子连边就好了

这样仔细一想完全可以体现前缀

所以这题做完了

code:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#include<queue>
#define ll long long
using namespace std;
const int MAXN = 2e5 + 100;
int n, na, nb, m, sz, a[MAXN], b[MAXN], isa[MAXN << 2];
char s[MAXN];
int lst, T, id[MAXN], last[MAXN << 1], f[MAXN << 1][20], ch[MAXN << 1][26], fa[MAXN << 1], len[MAXN << 2];
int in[MAXN << 2], home[MAXN << 2], to[MAXN << 3], nxt[MAXN << 3], ccnt;
vector<int> g[MAXN << 2];
ll dis[MAXN << 2];

inline void ins(int c) {
	int p = lst, np = ++T;
	lst = np;
	len[np] = len[p] + 1;
	for(; p && !ch[p][c]; p = fa[p])ch[p][c] = np;
	if(!p)fa[np] = 1;
	else {
		int q = ch[p][c];
		if(len[p] + 1 == len[q])fa[np] = q;
		else {
			int nq = ++T;
			len[nq] = len[p] + 1;
			memcpy(ch[nq], ch[q], sizeof(ch[q]));
			fa[nq] = fa[q];
			fa[q] = fa[np] = nq;
			for(; p && ch[p][c] == q; p = fa[p])ch[p][c] = nq;
		}
	}

}

inline void judge(int b) {
	int l, r;
	scanf("%d%d", &l, &r);
	//读入l,r字符串区间
	r = r - l + 1;
	l = id[l];
	//前缀所在节点
	for(int i = 19; i >= 0; --i) {
		if(f[l][i] && len[f[l][i]] >= r)l = f[l][i];
	}
	//树上倍增,找到他真正表示节点
	isa[++sz] = b;
	//这一步其实是拆点了
	len[sz] = r;
	g[l].push_back(sz);
	//前缀所在节点记录一下
}

inline bool cmp(const int &x, const int &y) {
	return len[x] > len[y] || (len[x] == len[y] && isa[x] > isa[y]);
}

inline void ct(int x, int y) {
	to[++ccnt] = y;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	in[y]++;
}

inline void solve() {
	scanf("%s", s + 1);
	n = strlen(s + 1);
	lst = T = 1;
	for(int i = n; i >= 1; --i)ins(s[i] - 'a'), id[i] = lst;// printf("%d? ", lst);
	//puts("");
	for(int i = 1; i <= T; ++i)f[i][0] = fa[i];
	for(int j = 1; j <= 19; ++j) {
		for(int i = 1; i <= T; ++i) {
			f[i][j] = f[f[i][j - 1]][j - 1];
			//树上倍增部分
		}
	}
	scanf("%d", &na);
	sz = T;
	//printf("%d!!\n", T);
	for(int i = 1; i <= na; ++i)judge(1), a[i] = sz;
	//第一类串,我们强行定位,sz是定位后对于isa和len数组位置
	scanf("%d", &nb);
	for(int i = 1; i <= nb; ++i)judge(0), b[i] = sz;
	//再招每一个b串
	for(int i = 1; i <= T; ++i)sort(g[i].begin(), g[i].end(), cmp);
	//对于每个点排序
	for(int i = 1; i <= T; ++i) {
		int lst = i;
		//找到lst
		for(int j = g[i].size() - 1; j >= 0; --j) {
			int nw = g[i][j];
			//提出节点,注意这里是反序的...所以应该可以把cmp改改变正序
			ct(lst, nw);
			//从最近B向他连边
			if(!isa[nw])lst = nw;
			//如果终末点是b号点
			//我们就拿b号点作为最近终末点搞一下
		}
		last[i] = lst;
		//记录他最近是哪个b节点
	}
	for(int i = 2; i <= T; ++i)ct(last[fa[i]], i);
	//父亲最近的b向i连边
	for(int i = 1; i <= sz; ++i)if(!isa[i])len[i] = 0;
	//b节点len清空
	scanf("%d", &m);
	int x, y, f = 0;
	ll ans = 0;
	for(int i = 1; i <= m; ++i)scanf("%d%d", &x, &y), ct(a[x], b[y]);
	//直接按照支配关系连边
	queue<int> q;
	//唯一看得懂的部分啊
	for(int i = 1; i <= sz; ++i) {
		if(!in[i])q.push(i);
	}
	while(!q.empty()) {
		x = q.front();
		q.pop();
		ans = max(ans, dis[x] + len[x]);
		for(int i = home[x]; i; i = nxt[i]) {
			int v = to[i];
			dis[v] = max(dis[v], dis[x] + len[x]);
			if(!--in[v])q.push(v);
		}
	}
	for(int i = 1; i <= sz; ++i) {
		if(in[i]) {
			f = 1;
			break;
		}
	}
	if(f)puts("-1");
	else printf("%lld\n", ans);
	while(!q.empty())q.pop();
	for(int i = 1; i <= T; ++i)fa[i] = 0, memset(ch[i], 0, sizeof(ch[i]));
	for(int i = 1; i <= sz; ++i)g[i].clear(), isa[i] = len[i] = home[i] = dis[i] = in[i] = 0;
	lst = T = sz = ccnt = 0;
}

int main() {
	int T;
	scanf("%d", &T);
	while(T-- > 0)solve();
	return 0;
}

夏晓光(loveJY)的博客

CF536D Tavas in Kansas