夏晓光(loveJY)的博客

NOI online #1 T1
T1就不会做

小 D 有一个长度为 $n$ 的整数序列 $a_{1 \dots n}$​，她想通过若干次操作把它变成序列 $b_i$​。

小 D 有 $m$ 种可选的操作，第 $i$ 种操作可使用三元组 $(t_i,u_i,v_i)$ 描述：若 $t_i=1$，则她可以使 $a_{u_i}$​​ 与 $a_{v_i}$​​ 都加一或都减一；若 $t_i=2$，则她可以使 $a_{u_i}$​​ 减一、$a_{v_i}$​​ 加一，或是 $a_{u_i}$ 加一、$a_{v_i}$ 减一，因此当 $u_i=v_i$​ 时，这种操作相当于没有操作。

小 D 可以以任意顺序执行操作，且每种操作都可进行无限次。现在给定序列与所有操作，请你帮她判断是否存在一种方案能将 $a_i$ 变为 $b_i$​。题目保证两个序列长度都为 $n$。若方案存在请输出 YES，否则输出 NO。

这个题的暴力就不说了吧,有60分呢

正解是图论

把$b_i->b_i-a_i$,这样$a_i$==0,目标是清空序列

然后我们在图中的点比较显然,就代表$b_i$这个值,然后你会发现对于2类操作,他的影响是把一个点的权值运送到另一个点,那么我们会发现同一连通块内所有点的权值都是可以互相运送的,所以如果存在一个连通块他的权值和等于0就可以把这个连通块削成0

而1类操作的影响好像就是总权值会变了qwq,我们这样连:(bel_{u_i},bel_{v_i})如果一个连通块内部有这样的边而且连通块权值和还是偶数的话这样的连通块一定可以削成0

还是不够,我们把上图2类边带来的连通块缩点,然后再考虑1类边能不能带来转运权值呢?显然可以,如果两个点之间有长为偶数的路径就一定能够转运权值而不影响其他点

你会发现这样的部分一定是个连通块里面有奇环/jk,而且只需要连通块里面有一个奇环就可以,这样一定可以有偶数的路径(图中好像花成奇数了?)

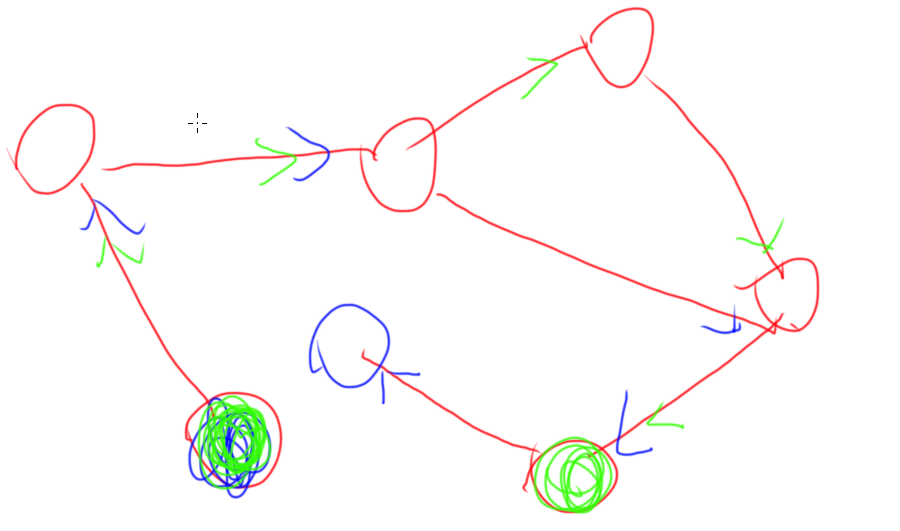
证明就是我们可以走奇环改变路径长度奇偶性

不含奇环的一定是个二分图,然后我们把它二分图染色,得到黑白两组,黑白组内部一定可以互传权值,而跨组只能同加同减,这样的连通块有解的条件:

1. 权值和为偶数且tag==1或者为奇连通块
2. 没有内部边的话(tag==0)黑白点权值和相等qwq

然后就做完了!

code:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#define ad1(x,y) (ct1(x,y),ct1(y,x))
#define ad2(x,y) (ct2(x,y),ct2(y,x))
using namespace std;
#define ll long long
const int MAXN = 1e6 + 7;
struct rec {
	int u, v;
	rec() {}
	rec(int a, int b): u(a), v(b) {}
} e[MAXN];
int ccnt, cccnt;
int home[MAXN], nxt[MAXN * 3], to[MAXN * 3], first[MAXN], fnxt[MAXN * 3], fto[MAXN * 3];
int bel[MAXN], bw[MAXN], sum[MAXN], a[MAXN];
bool tag[MAXN];

inline void ct1(int x, int y) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
}

inline void ct2(int x, int y) {
	cccnt++;
	fnxt[cccnt] = first[x];
	first[x] = cccnt;
	fto[cccnt] = y;
}

inline void dfs1(int u, int c) {
	bel[u] = c;
	sum[c] += a[u];
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(!bel[v])dfs1(v, c);
	}
}

bool dfs2(int u, int c, bool &t, ll &sb, ll &sw) {
	if(~bw[u])return bw[u] == c;//之前已经有颜色了
	bw[u] = c, t |= tag[u];//有一个一类边的连通块为1就好
	if(c == 0)sb += sum[u];//黑点权值和
	else sw += sum[u];//白
	bool ret = 1;
	for(int i = first[u]; i; i = fnxt[i]) {
		int v = fto[i];
		ret &= dfs2(v, c ^ 1, t, sb, sw);//走着,一个不行就不是二分图
	}
	return ret;
}
int T;
int main() {
	scanf("%d", &T);
	while(T--) {
		int n, m, p = 0, k = 0;
		scanf("%d%d", &n, &m);
		for(int i = 1; i <= n; ++i)scanf("%d", &a[i]);
		for(int i = 1, x; i <= n; ++i) {
			scanf("%d", &x);
			a[i] = x - a[i];
		}
		memset(first, 0, sizeof(first));
		memset(home, 0, sizeof(home));
		for(int i = 1, t, u, v; i <= m; ++i) {
			scanf("%d%d%d", &t, &u, &v);
			if(t == 1)e[++p] = rec(u, v);
			else ad1(u, v);//第一次缩点
		}
		memset(bel, 0, sizeof(bel));
		memset(sum, 0, sizeof(sum));
		memset(tag, 0, sizeof(tag));
		for(int i = 1; i <= n; ++i) {
			if(!bel[i])dfs1(i, ++k);//真的缩点,无向图缩点不需tarjan
		}
		for(int i = 1; i <= p; ++i) {
			if(bel[e[i].u] == bel[e[i].v])tag[bel[e[i].u]] = 1;//打标记
			else {
				ad2(bel[e[i].u], bel[e[i].v]);//这个2类边
			}
		}
		memset(bw, -1, sizeof(bw));
		bool ans = 1;
		for(int i = 1; i <= k; ++i) {
			if(bw[i] == -1) {
				bool tg = 0;
				ll sumb = 0, sumw = 0;
				if(dfs2(i, 0, tg, sumb, sumw)) {
					if(tg)ans &= ((sumb + sumw) % 2 == 0);//如果有1就一样
					else ans &= (sumb == sumw);//否则黑白点权值要相同才行
				} else ans &= ((sumb + sumw) % 2 == 0);//不是二分图只需权值和为偶
			}
		}
		puts(ans ? "YES" : "NO");
	}
	return 0;
}