P6383 『MdOI R2』Resurrection

洛谷4月月赛Div1T2

这道题确实真思维题

突然想起NOIP出的树上的数...辣么一道毒瘤思维题....我好怕啊

所以还是要善良

显然的东西:

根,肯定要定在n号点,要不然题目中给出的奇特性质就用不上了

~~之后你会发现从每个点到根他的祖先编号递增?~~

不显然的东西:

上去直接猜结论:

任意两条新树中的边放在原树中不会相交

即: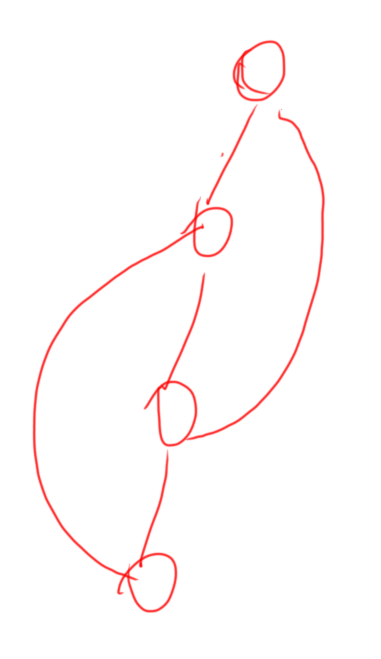不会出现

考虑证明这个结论是充要的

必要性...显然吧,如果图中第1,3个点想要连边,那么在1上的那条边被断开的时候1_{3不能有边断开,而且3}父亲的边一定要断开,所以和2~4矛盾啊

再考虑怎么构造出一种合法方案,这样就充分了

然后我们把根放入一个堆里,做一下流程

从堆中取出编号最小的节点,断开原树中与父亲连边,再把他新树中的儿子节点加入集合

这样构造的一定合法

所以每个点都会向他的祖先连边,而且如果向x级祖先连边那么1~x-1级祖先他的子树中点就都不能连

考虑f[i][j]表示i向上有j个可以连边的祖先,子树里连边的方案数,那么我们枚举一下x,然后i->x连一条边,这样子树里的点就都不能向1~x-1连

方程就是这样的

f[i][j]=\sum_{x=1}^{j}\prod_{v\in son(u)}f_{v,j-(x-1)+1}

转移可以前缀和优化

没了

code:

#include<iostream>
#include<cstdio>
#include<cstring>
#define CT const int&
#define ll long long
const int P = 998244353;
const int MAXN = 3456;
int n, u, v, f[MAXN][MAXN], p[MAXN], ccnt;
int home[MAXN*2], to[MAXN*2], nxt[MAXN*2];

inline void ct(CT x, CT y) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
}

void dfs(int u, int fa) {
	// printf("%d?\n", u);
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v != fa)
			dfs(v, u);
	}
	for(int j = 0; j <= n; ++j)p[j] = 1;
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v == fa)continue;
		for(int j = 0; j <= n; ++j) {
			p[j] = 1ll * p[j] * f[v][j] % P;
		}
	}
	for(int i = 1; i <= n; ++i)
		p[i] = (p[i] + p[i - 1]) % P;
	//求一个前缀和
	for(int i = 0; i <= n; ++i)
		f[u][i] = (p[i + 1] - (u == n ? p[0] : p[1]) + P) % P;
	//因为是前缀和所以要减掉p_1
}

int main() {
	scanf("%d", &n);
	for(int i = 1; i < n; ++i) {
		scanf("%d%d", &u, &v);
		ct(u, v);
		ct(v, u);
	}
	dfs(n, 0);
	printf("%d\n", f[n][0]);
	return 0;
}

夏晓光(loveJY)的博客

P4428 [BJOI2018]二进制