夏晓光(loveJY)的博客

B

对于一个串长的位置是需要二分答案的,否则串数的复杂度就是$O(n^2)$的...

然后选的两个串靠后的串至少起始位置靠左啊...

然后就是一个lcp>=l

能否在一个区间中选两个前缀lcs>=一个长度

考虑建一个SAM,然后考虑一个点C,对于C来说他本质相同的字符串在其子树a,b中

如果我们把两个前缀,第一个前缀的位置作为x坐标,第二个前缀的位置作为y坐标

那么对于两个前缀他的lcs作为这个点他的值,此时我们有n^2个点

而且这两个子串a,b他们在向父亲合并时就构成了一个新的

显然对于一个SAM上节点,所有的endpos中只有相邻的有用处(贴的最近)

那么就是对于一个点y来说在c中查询一个前驱后继只有两个点能作为答案(点)

那么和并两个子树就相当于一个启发式合并的复杂度了.....

也就是说实际上我们这样的点只有nlogn个

然后再回到mlogn个询问上来,如果把他们拍到平面上,每个询问就都是一个区间是否有个正方形内某个数的值大于len,其中我们左端点是L+len-1

这个就是二维数点了,主席树,当然也可以用扫描线+线段树轻松离线解决!

C

当i增大到一定程度时答案会变成一个等差数列的形式...

然后我们就可以强行在某个位置开始用等差数列解决.....

艹这显然是错的但是很能拿分

其实我们对于边权很小的情况我们可以考虑把每条边的权值拆开变成贡献来算...

然后我们有个问题就是对于前i层点可以搞出一些东西,然后第i+1层点可以基于前i层点去操作

那么显然是前i层有一些点已经连通了,第i+1层点再连会导致一些边使得成环,就要断掉

然后对于贡献就很显然了,考虑对于权值为w的,我们把0~w-1的加入后每个都算他一遍,那么他就会被算w遍,正好和他的权值是w对应qwq

A

dp + 多项式

没了

讲课:...

T7

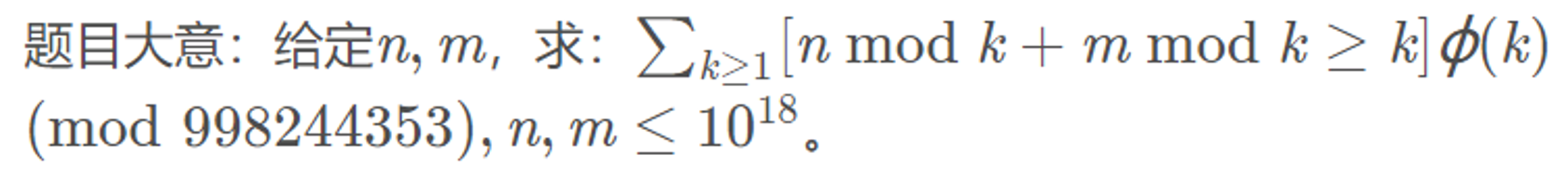
(n+m)/k会进位,而且进一位$=[n/k+m/k+1]$

那么这个性质其实就是$[n$分为三项

把其中一项单独提出来!

$\sum_{k>1}\frac n k \phi(k)$

$\sum_{k=1}^n \sum_{d|k} \phi(d)$

$\sum_{i}^n i$

$=\frac {n*(n+1)} {2}$

所以把每个"n"带进去化简一下就是n*m....

T16

首先对于一个C就能得到一个特定答案..

然后所有可能的C好像只有$={P-w_i-1,i \in (1,n)}+T$

那么我们完全可以先二分一下(我们选一个边额外的收益)然后O(n^2)check一下,就是钦定C然后dp

考虑设F[C]表示 确定C的答案那么相当于找这个F数组的最大值

确定这个数组一个位置需要花费O(nlogV)直接做是$O(n^2logV)$

我们可以先考虑计算出$F_{C_1}$然后对于下一个就是如果比他小我们根本不用考虑计算,如果比他大则需要计算出新的值

然后就可以发现对于一个随机的排列最多有logV次会比前面大,

那么就可以随机一个C的排列然后就能做了...我们至多计算logV次某个数组精确最大值

T21

dp,然后转移是一个区间....

$f_i=max_{i-r<=j<=i-l}f_j+sgn(S_i-S_j)$

然后这个显然是可以维护一个以S为下标的线段树,然后以j为下标的单调队列去记录$f$这样可以做到O(nlogn)

显然值域是O(n)级别的

因为有用的只有f_j,f_j-1所以显然对于他们来说前缀和越小越好qwq

对于每个f值可以维护一个S的单调队列

然后全局所有的f值(还有一个区间的限制)可以维护一个总的下标的单调值就行了

T20

首先对于每个k可以做到O(nlogn)就是都放进去然后拿深度最大的没被标记的点再,把k级祖先拿出来标记,重复这个过程

而对于k比较大可能删的比较快...

然后就发现答案差不多为$ O(x+(n-x)/k) $然后这个东西主要在于x,其他的部分是调和级数

所以只需要把他叶子距离为k的点初始化进堆做那个贪心就好了...剩下的就是一个调和级数了....

复杂度可能是$O(nlgn\ln n)$

T15

两个人,一开始有x,y颗石子,对着拿,每轮拿a_i个,不足全拿,带修a_i,x,y问每次n轮之后最后第一个人手上剩余多少石子.....

维护一个折线图,和x+y取min,和0取max

如果这个折线图的极差要大于上下边界差那么碰一次壁就和之前的无关了

如果极差太小那么我们既不碰上边界也不碰下边界

那么就可以统计一个区间的前缀和,对于初始在哪里计算个答案....

在一个范围内我们会碰上边界,初始值无关,我们只需要算区间中某个值的答案即可

那么只有一个小区间我们是需要维护的,所以就可以考虑线段树和分治...维护维护修改和查询

T13*

结论1,次数不重要

结论2,二分答案

结论3,这个有博弈论结论.如果有一张二分图g,一开始在S集合中,每个人可以移动一步不能动就输

那么一个点先手必胜当且仅当所有最大匹配都经过他

所以本质上我们把a,b排序

第x行第y列看成a_x+b_y,列出一个网格

如果a_x+b_y<=二分的值,

那么网格会成为一个折线满足...

那么每次我们回跳到同一行同一列的白点或黑点

那么问题就变成了每个点每个点向他同行同列连边....是否有最大匹配

转化成最大独立集

所以可以发现白点一定是在某个分界点左上角...黑点在右下角

然后就可以考虑二分一个增量,对于增量从上到下从左到右

是单调变化的,所以可求出那个最优划分点.......

T11*

多项式可以发现我们在不知道R的时候能算出一个东西

所以就可以先和C点乘一下,再和R做点乘

考虑分治,显然C有用长度小于等于区间长度

那么我们每次都是从C中除以一个L的操作,???

总区间的C/右边的L就可知左边的R了....

所以我们就可以先递归左半部分再递归右边部分最后能得到底层的R是那个单项式

T6

通信题md

随机一个长数列,然后这个长数列大概率一些东西异或起来可以表示出一个线性基

那么我们猜任意110个数字能构成一个线性基,然后我们只用这些数字就可以搞搞

B然后是1就异或是0就不关

三个一组,如果有一个位置被ban掉了就考虑

000 001 010 011 100 101 110 111

1 : 001/110 即考虑那个被ban掉了

0 : 100

第一个位置被ban掉了

010 -> 00
011 -> 11

然后反正就是这样设置下去,用三分组的方式构造....

T5

dp_{i,j}表示我走到i,然后目前收益为j的最小代价

那么这个剩余可以的代价要小于等于m/j...就调和级数了

T1错题

m<=n+300

最多300个环

度数之和=2m,那么也就是说$ \sum_{d-2}=2(m-n)$

$\sum_[{d-2}]<=2(m-n)$

度数大于等于3的不超过600个...

那么我们就可以考虑就是一堆链...链数是O(m-n)的

然后对于链外的关键点可以暴力

而链上的点我们还要求最短路可以考虑枚举一个分界点....

啊,然后他萎了

T9

Hall定理,一个二分图存在完备匹配,左边选出一些点来,然后右边的点存在完美匹配的充要条件是左边任意一个点集都有完备匹配

对于一个确定的A,B就可以连边然后考虑左边连a_i右边连b_j然后就是一个中间连边了...

最大流怎么转换成最小割...显然存在一个最小割我们可以把他们都割掉

最小割至少能做到\sum_{b_i}

然后我们想能不能dp一下这个右边的方案

然后要什么统计割一定要大于最小割....就是前缀和>=某个数...

T17

靠...

g是f的k次卷积,求g的前缀和

首先把x拆成k个部分,每个x_i都用m的次幂表示出来

然后下课了....