A

最大值就是每一条横线每一条竖线都达到两边点数较小值*2

对于n是偶数的时候

我们跳不到最大值

尝试达到最大值减2

对于n是奇数的时候

发现我们可以分类讨论

B

ans=点-边+环

然后对于平方和可以用线段树

C

对于一个数字x,R(x)他们在膜B-1意义下是一样的

所以我们可以想办法处理出一个数组f,就是表示有一个区间在%B-1意义下是x

枚举右端点,看左端点有哪个位置,这样有O(nB)的复杂度

处理出f后可以再处理一个g

B-1和0在%B-1意义下都是0

如果一个序列的只有一个位置不是0位B-1可能会有问题,然后我们特判掉就好了

$R(x)=\sum_{x_i}*B^i$

而$B^x-1$可以因式分解出一个B-1....

就是说$B^i-1=(B-1)*(B^{i-1}-B^{i-2}-B^{i-3}.....-1) \equiv 0 mod (B-1)$

原来是y,在mod 意义加+x-y

那么考虑能否在S中找到一个数组差值为x-y

可以几个f(S,x)满足包含的为S,他们的和为x,区间个数

对于一个固定的右端点他的取值至多会有B种,所以我们预处理也是O(nB)的

然后再搞一搞0的情况

并且从y和输入的S转换出一个T来回答询问

字符跳动ACM赛题目串讲!

没有集训队作业是有个150的老哥....

C1A

建一个图,然后能交换就连边

考虑如果一个pos和val不在连通块就不行

否则拉棵生成树出来交换叶子,暴力搞搞n^2就好了

就是类似于冒泡排序的那种方式,我们显然一个数到他该到的位置不会花太多代价,而他给了$n^2/2$次

C1B

建AC自动机,然后把所有不合法的位置标志出来,一个点的fail不合法那么他也不合法

然后不经过不合法位置方案数??矩阵快速幂就好了$O(|S|^3logL)$

C1C

点权排序依次加入,维护size最大连通块

C1D

次数对于2取模说明我们可以用longlong来表示多项式

多项式带余除法....

$P(x)=x^{32}+x^{26}+x^{15}+x^{7}+1$

再看看样例

发现$x^{2^32-1}mod P =1$

$x^i$的逆元就是$x^{2^32-1-i}$

能够求逆发现就能够BSGS

预处理出$x^{KS}$和$x^K$,以及他们的逆元,BSGS

$O(\sqrt{TN}logN)$

C1E

回文树

一个串本质不同的回文子串是O(n)级别的

可以尝试DP

dp_i表示以i开头的

$p_s$表示以S去掉开头结尾各一个字符后得到字符串,$b_s$为s最长回文前缀,均用回文树节点表示

已经得到了第i个串$S_i=t$考虑按照下面步骤得到剩余串

1.结束套娃或者$t=p_t$并来到第二歩

2.$t=p_t$重复第二歩或者到第三步

3.$s_{i+1}=t,i=i+1$并回到第1步或者令$t=b_t$到第四步

4.$t=b_t$重复本步或者令$s_{i+1}=t$并回到第一步

一共这样四步,放在回文数上从小到大DP

C1F

有用的状态不会很多,首先集合内部没法拆分,可以考虑整数拆分

然后f(S)表示当整数拆分为S时他的期望是多少

P(AB)表示从局面A转移到局面B的概率

然后发现这个只有自环和DAG

怎么算$P(A,B)$

先枚举一个B尝试所有能得到B的集合A

所以可以考虑枚举一个大小为k的B子集C,C要枚举不重复的子集,然后用C和B-C里面的配对

就可以得到这个情况下合法的A,顺便算出概率

C1G

随机240个排列,然后对于交互库里面那个排列退火

然后首先找一个排列$P_1$,随机更改m个位置的到$P_2$然后交互库返回的几位D1D2

因为对于一个位置要么x-v1在a中出现,要么x-v2在B中出现

如果我们变的小于m次就重新随机,那么我们会发现对于每个位置就可以把可能的位置降为O(2m)排除了可行的n-2m个

m取到根号n就可以期望O(1)就可以让这些位置只剩下唯一解

$m=\sqrt(n)/2$最好

C1H

官方题解,建一个线段树在上面跑斜率优化,sb

上边界一定贴着一个$a_i$

先枚举一个$a_i$找左右第一个比他大的数,记为$l_i,r_i$

然后对于$[i,r_i)$中任意一个位置j用$(j-l_i)a_i$

而$[r_i,n]$任意一个位置用$(r_i-l_i-1)a_i$更新答案

只需要支持区间插入单点求max可以用李超树qwq

C1I

模拟题

C1J

不考虑旋转就是nim游戏

矩形的mex就是sg_i表示i的,$sg_i$不小于$sg_j$,$sg_i=maxsg_j+1$,直接二维数点

那么相当于每个矩形都有一个$a_i$或者$b_i$,异或起来等于0

假设都不选a_i都异或下,$b_i$就成了a_i^b_i,但是线性基要输出方案

考虑线性基中每一个数怎么输出方案,其实就是每个数记录一下异或的是哪些基...

反正又西伯利亚题了

C1K

我们强制1和2不相同3和4不相同....这样我们会发现如果再把那个n组的限制连上去,你会发现我们一定是偶数环...是二分图

而且度数为2好像可以很快的解决匹配

所以一定有解O(n)

C1L

V-E+F=1

那么其实就可以考虑求面数=求点数和边数

k重交点会让点数+1

面数+2k,而一条线段会被两端点算两次

相当于边数+k,一条直线两端形成的射线会被少算一次再加回来

最后特判下椭圆的情况

C2A

因为m<=100

连续段数量不超过1000...

维护连续段即可

C2B

离线然后分块$O(q\sqrt{n})$

中序遍历是否单调

然后可以考虑什么数据结构支持修改和查询,线段树吧

改x的点权只会影响其到根的路径上一些子树是否为二叉搜索树,

然后判断是log的所以$O(nlog^2n)$

C2C

可以考虑五维

f_{i,j,k,l,m}表示前i个数j,k,l,m4个1的位置

前面L个不足4就把剩下的填-1

容易发现状态数是2^L左右的

然后DP即可,发现不会很大$\binom{L}{P}$

C2D

一个可行区间为l,r的相加得到的为$[l1+l2-1,r1+r2+1]$

相乘也一样啊,就是区间范围相乘了

$f_l$表示得到的数左端点为l时右端点最小是多少,转移用定义...

$f_x=x,f_y=y$

$O(n^2)$

C2E

直接求虚树

C2F

分治...

solve(n,k)表示进行到2^n那个矩阵的答案

会发现我们和某个直线一定会两个重合,就是转化成本质相同的

然后始终我们剩下的都只会有一个直线(或者两个也行)

一个就是下面这个

C2G

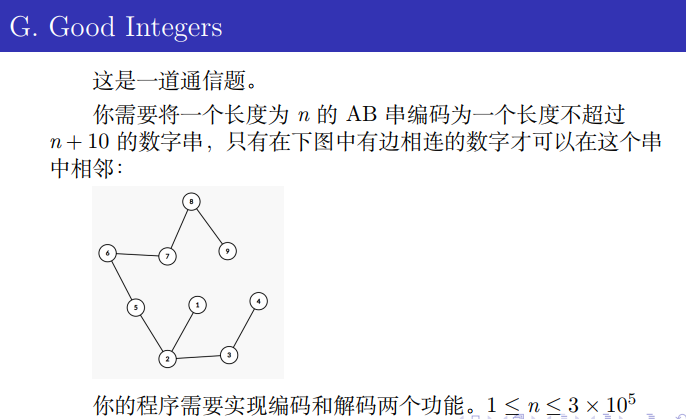
通信题

阴间题

构造自动机,然后每个点只会有AB两个出边,然后转码数字串就直接把路径上的所有数字输出出来。

C2H

权值线段树

C2I

\sum_{i=0}^n{ia\b}可以用类欧

然后对于带根号的那个东西就可以用SBT在1e9范围内找一个最相近的分数逼近他,每走一步精度增加指数级

复杂度O(Tlogn)

就解决了,然而我还是不会类欧

感觉没有那个T可以直接凸包拟合

C2J

裁判可以划分为两个阵营,冲突的连边

然后对于裁判求最大独立集

C2K

按照他的方法随机生成几千张图,那个序列在这个图上退火

找个优秀的输出

C2L

把所有的公切点拿出来求一个凸包,然后得到这个n个圆形成的凸包,然后圆弧都变成了直线

再沿着这个凸包边界枚举找最长的一个圆弧即可

C2M

考虑建出一个trie树,然后LCP为树上LCA深度

然LCP(s,t)=1/2(|S|+|T|+LCA(S,T))然后d就有了

问题就是最小化

2(\sum_{i=1}^{n|t_i|)-\sum_{i=1}}{n-1}d(t_i,t_{i+1})-|t_1|-|t_n|

把树根当做$t_0$就是最小化

$\sum_{i=1}^n d(t_i,t_i+1)$

最后就是一个所有点到重心的距离之和

带权重心!