夏晓光(loveJY)的博客

A

积性函数F{x}前缀和

找一个G(x),满足两个条件

1.很好求前缀和

2.能定义$f(p^q)$

3.g(p)=f'(p)

流程

另$h=f/g(x)$,为狄利克雷除法

$h*g=f$怎么求呢?

会发现仅当所有质因数的指数都>=2时才能h不为0

所以当

h(p)大概率为0,仅当h(p)!=0时只有最多根号p个...

$\sum f(x)=\sum_d h(d) \sum_{i=1}^{n/d}g(i)$

发现h(d)最多仅有根号个不为,然后后面整除分块差不多是根号log的

回到这个题,发现其实$2^{F_i}$是在枚举i的质因子集合的子集,改为枚举这个子集k,然后有$\lfloor n/k \rfloor$个数字包括这个集合

$\sum_{k=1}^n\sum_{d|i}\mu(d)^2$

$\sum_{i=1}^n\sum_{d|i}\sum_{k^2|d}\mu(k)$

这一步转化其实就是枚举了平方因子然后容斥掉了,就是说平方项只会被统计了一次

$\sum_{k=1}^{\sqrt{n}}\mu(k)\sum_{k^2|d}\frac n d$

$\sum_{k=1}^{\sqrt{n}}\mu(k)\sum_{i=1}^{\frac n {k^2}}\frac n {ik^2}$

B

部分分:不强制在线等价于不可持久化

很点分治,确实

边询问边修改就动态点分治一下(点分树)

用一颗线段树维护点分树内部到其最近的儿子的距离

然后查询的时候暴力向上跳然后加上一些东西就好了,所有的取个min

每一层可以暴力开

然后我们可以发现可持久化就每次改下点到根所有的....

C

首先发现我们可以随机一个排列,然后下标向权值连边

可以设dp[i][j]表示前i个点导致形成j个环的方案数

然后转移其实可以考虑枚举最后一个环大小然后用个组合数

然后你会发现对于大于k的单独循环点是可以直接计数的

dp是之前那个博客里的原题题解

官方题解:发现其实答案是2k次多项式,因为我们要求个前缀和

拉格朗日插值即可

C3A

钦定构造出的数列单调不降

然后$a_1=1$分类讨论

$k<=n+1$

最后k个元素填入$x+a_i$中间放$a_1+1$

否则$a_2=x+a_1$并让k-(n-1)重复这个过程

最大元素为$1+x(n-1)<1e6$

C3B

任意一个矩形都可被至多6个长宽为$2^k$的正方形覆盖

所以可以写一个二维ST表,然后每个表记一个最小生成树,然后合并时直接把生成树合在一起暴力O(n)

那么记录的时候可以避免sort

O(nRClog(R+C)+Qn)

C3C

两端拿出,中间求个lcm即可

注意判断是否合法

C3D

毒瘤

后手一定可以把先手逼到边远上去

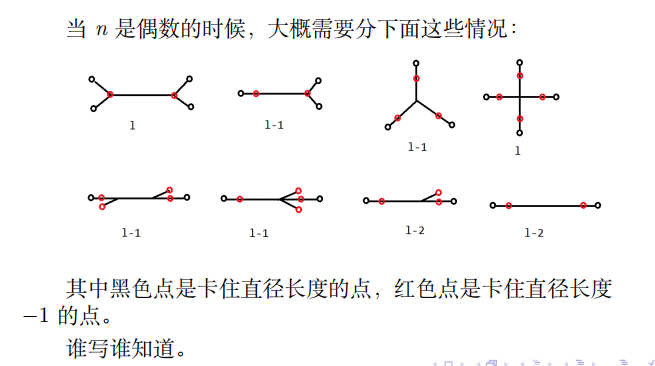
如果n为奇数,存在两条直径答案是直径否则是直径-1

n是偶数,直径长度为l,答案可以为l,l-1,l-2

第一种是

直径两头都是叉,l

第二种是,只有一个直径是叉,l-1

第三种是分了好几个叉,三个或者分了四个叉,l-1,l

第三个是卡到直径-1的情况...

C3E

只允许加成

可以考虑d进制,然后就能够表示了!

然后12个数不够用

所以我们可以再考虑-

考虑2d+1进制每个写成$\sum_i {x_i(2d+1)^i},x_i$是个实数绝对值小于等于d

d=3为例,就能够7^0....79这些都有了

然后再造出2,3

那么所有的都有了

$84996=7^6-2*7^5+3*7^3-7^2-3*7^1+2*7^0=(7^6-7^2)+2*(7^0-7^5)+3*(7^3-7^1)$

C3F

四个角圆心在哪里才会成为圆上的点

显然把垂直平分线把整个矩形分成4部分,每个部分分别处理

然后一个点在圆外就是其圆心位于垂直平分线另一侧

把中间两条线拿出来,答案一定在这两条线上:竖直分割线和水平分割线

对于矩形的四分之一,他的答案一定在其界上

然后就是一条半平面就是一个区间+1就可以直接做了...

C3G

A找一个最小循环节

然后对于每个给定的字符串尝试匹配一下每个A中的位置,从匹配起点向终点连成一个边权为1的有向边

问题变成了500个点的图找最小环,直接Floyd

C3H

求个下界

如果行和列都形成1~n的排列,两维坐标排序

答案至少是$\sum_{i=1}^n|x_i-i|+\sum_{i=1}^n|y_i-i|$

然后发现一定不会相撞,所以就是答案

C3I

反弹看做穿过,循环叫做2l

考虑某个时间t是否合法

所以考虑最多可能有两个目标位置在t时可到达

然后就二分图完美匹配,发现每个点度数最多为2,O(n)即可判断

只可能是若干条链和一个环

然后枚举时间T然后chk,任意一条边至多只会在4个时刻出现,总边数$O(n^2)$

而一条边只会有4个时刻出现,所以有用的时间不多

$O(n^2)$

C3J

最小的非零的数

每个数可写成对二取模的生成函数

F(x),G(x)\in S F(x)+G(x)\in S

然后答案就是F1(x)x^k1+F(x)xk2.....去掉末尾的x得到的最小结果

这就是个线性组合

答案就是多项式gcd

gcd满足可加性每个区间分别记录gcd

每个区间维护能得到最小元素,两个元素合并直接暴力

多项式取模就是辗转相除法

合并时最高位补齐再^再补齐再

时间复杂度O(nlognlogA)

感觉他们说如果长度大于63就答案是0因为我们能叉出线性有关一定就是0,否则就是1

但原题说是最小非0

C3K

首先二分答案,判掉奇偶性

然后一堆东西按照x排序可以cdq分治,

然后按照x排序后,再按照y排序就变成了插入某个点距离最近的是否存在不符合的...

首先我们按x后再按ycdq然后推推式子就是

$x_0-x+y_0-y>=|z_0-z|$

$x_0+y_0-z_0>=x+y-z$

$x_0+y_0+z_0>=x+y+z$

这个过程可以归并O(nlog^2n)

C3L

注意到最高位77777700000001

和12345700000001是一样的,直到最高位最大的7发生进位

设$f_{i,j,k}$表最大值为i后面有j步,然后第一次进来的时候末尾是k的情况,发生进位需要多少步,再设$g_{i,j,k}$表示进位后最后一位是多少,转移可以有j-1重复10次进位得到

可以根据这个dp每次进一位

会发现这个模数可能加爆,可以求出把它加爆的步数,顺便求出加爆后得到什么数

然后容易发现转移成环,所以我们可以快速跳过一些环,最后剩余的部分套用不取模的算法

若干个log

C4A

首先判断一下有回路充要条件,就是每个点度数必须都是偶数

然后权值不同的出边两两配对变成一个点,拆开点后我们能得到很多个环,然后我们可以把他们合并

然后考虑两个环同时经过点u,设环中第一个和u相邻的边为e_1,e_2第二个环中为e_2e_2'合并时两种方案一定有一个合法否则一定矛盾

不断重复这个过程缩环即可

C4B

这个考虑三个点的叉积是一个关于t的二次函数

所以可以发现每条边作为凸包上一条边是有一个时间区间的

然后对于一个边为面积的贡献可以用叉积算,并且只在一个区间内有一个二次函数加

然后就是一个区间加二次函数

然后就是每个时间二次函数求最大值

然后对于n+1个停止的时刻将时间轴分为n份同时做一次就可以了

复杂度$O(n^4logn)$

C4C

本质不同的圆最多有1330个!

对于每个圆

可以随机一个点,然后向外面走一eps向内走一eps

如果差值为k说明有一个类型的圆是k个,因为其他的都不包含他

所有我们有一个3660次的做法qwq吊锤std

C4D

然后我们可以发现10个时刻可以让每个手指移动到任意位置所以我们只需要压前十个时刻的决策

每个时刻的状态分三种

1.移动某个手指一步

2.有某个手指按下了且该手指就在那个位置到现在没变

3.有某个手指按下了某个位置但手指在之后没按过

$f_{i,s}$表示前i位密码,前S个时刻的状态012

然后我们有转移就是考虑用10个时刻之内的手指还是10个时刻之前的手指

1.无事发生(其实是移动了手指)

2.有个手指按了键盘

由于我们密码按顺序按,所以可以计算出前面10个时刻按键盘的手指在哪个位置

然后如果前面10个时刻的手指能过来按一下就让他们过来

当然我们也可以考虑让10个时刻前的其他手指过来按,前提是要有

输出方案不可做

C4E

首先搞一个线性基

考虑线性基里面的元素有那些是线性相关的(虽然好像看起来矛盾....)

就是说我们把不在线性基里面的向量拿出来做一遍线性基表示

如果能有一个不在线性基里面的向量表示后某个线性基的向量没用上说明那个向量也是线性相关的

C4F

考虑怎么从度数为d,d+1,变成d,d-1

首先删除所有连接两个d+1的点的边(删之后不是d+1的点就别删了)

接下来d和d+1的边我们跑二分图完美匹配

因为剩下的d+1一定和d+1个度数为d的连边,所以我们能有完美匹配就能删掉边

这样重复直到有一个要求的点出现

C4G

最小点覆盖首先可以用最小割去做,就是考虑两排点向S,T连1的边,而中间之间连1的边

然后带权是不是可以费用流啊?就是在S连接的时候用上val,而T的连边用上val

这样会发现慢,而且我们没有充分利用流量这个限制,所以我们把流量改成$M-a_i$

M是$maxa_i$,这样流出来的最小割就是答案了qwq

C4H

没听过,直接上题解

C4I

没听过,直接上题解

C4J

首先我们把整个图用120°角三等分,

然后询问中间一个点,返回的角度向左120°向右120°这个240°的扇形才有可能是答案

这样我们砍掉了一些范围,再多做几次,直到砍掉范围大于180°就可以画一条折线切掉至少一半范围

会发现我们可以用度数,期望两到三次就能把整个凸包切掉一半

然后一直这样做下去即可

C4K

x拆点为$x_1,x_2$然后s向$x_1$连(1,-无穷),和一条(无穷,0),而x2向t连(1,-无穷),和一条(无穷,0),u1~v2连$(1,w(u,v))$

总增广次数不过n次,每次用dijkstra求最短路即可

Johnson,中间有负权的时候可以对每个边$h_u-h_v+len_i$

但是zkw还是最强大的

C4L

首先花至多3次空格移动到末尾

发现我们可以至少两次把一个B移动末尾

就是考虑第一次把B和B前一个字符过来

然后再用空格把B前字符移走

然后发现当剩两个B的位置会挂掉

就是B在1和i-1的时候,我们B前面没有字符

所以我们要最后分类讨论,这个不超过4步

C4M

折半搜索

把地图砍一半,然后爆搜出上半部分和下半部分,并算出中间接起来的连通性情况

C5A

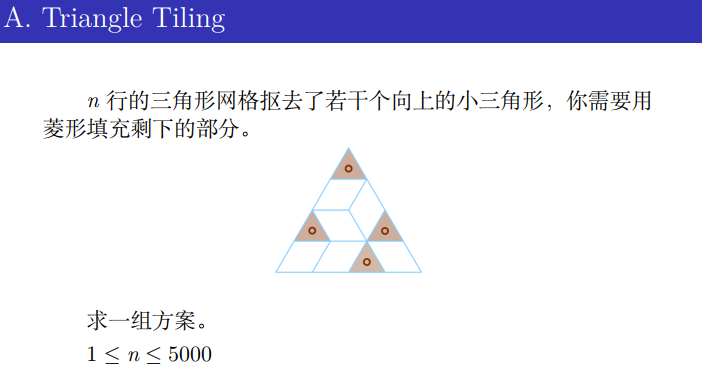
世界未解谜题

C5B

首先发现对于len=2的时候连续的0和1不同时出现,记1个数为a,而0个数为b

对于len变大的时候考虑缩串,缩法就是对于长度为>a/b下取整的串可以直接变成0,而长度度小于a/b的串可以变成1

然后你会发现我们每次只能朝着一个方向递归,也就是说1的数量确定了整个字符串就确定了...

所以可以找到所有长度为n的串然后枚举循环移位做匹配,显然可以bitset优化qwq

C5C

这题好像有点眼熟

C5D

完蛋了,感觉超级复杂

考虑乱搞,等价类不会很多...

写个程序爆搜,发现等价类数量不超过100个

说明我们可以打表

然后得到什么类型的,就可以知道某一个子串是什么类型的,也是每个类型有多少个子串,cnt数组乘一下

然后再发现我们能知道每个等价类个数就能做了

C5F

首先贪心选,然后直到任何一个数都会导致超过c,令c减去当前的和,然后选中的元素变成相反数,未选中的不变,-2e4~2e4,2e4的值域限制

所有数正负分开,正数前i个负数前j个和为k是否可行,复杂度$O(n^2c)$

注意到如果$f_{i,j,k}=1$那么$f_{i,j+1,k}$也是1对于固定的i,k$f_{i,j,k}$取值一定是前面一半0后面一半1

然后我们发现$f_{i,j,k}=1f_{i,j+1,k}=1$,所以我们可以只记01分界线就能完成此题

O(nc)

C5G

设f(x,y)表示x到s,s到y的最小权值

走路来转移,点重合不算

答案为f(t,t)

C5J

md是排列

然后你只需要记录前缀最小值,后缀最小值对于一个区间的mex就是不在他之中的最小的数

交互两个数的影响是O1的