省选模拟赛6

http://noi.ac/contest/341
qaq作业好多
qwq你p站也太强了吧绘画巅峰?

T1
每个点带代价的半径为K的园覆盖
首先我们联想到消防局的设立那道题,然后就有了20分贪心qwq
之后我们再去想优化这个贪心?不太行了,所以我们可以使用那道题另一个解法,动态规划
状态是显然的dp[i][j]表示点i向下j层已经被覆盖了的最小代价,然后你会发现这样没法转移,所以还要改一下
dp[i][j]表示点i向上j-K层已经被覆盖的最小代价,如果是负的就是向下
然后转移可以分成三类qwq
case 0:硬点
首先我们要保证一个基本事实,就是越优的越大,也就是说我向上能覆盖i就一定能向上覆盖i-1
所以在最后我们要集体向他前一个取min
这个状态的设计也是为了这个转移方便
case1: dp[i][K+1~2K]
钦定第二维是x
你会发现这样我们一定是在儿子的地方能覆盖到向下x-1的,这样我才能覆盖x
所以
case2:dp[i][0]
憨憨皮,这不是在点i放一个吗
那他的转移不就是下面点的dp[v][2K]之和吗
case3:dp[i][1~K]
烦死了,这个最麻烦....
首先你要认识到我们是在儿子处放上了某个东东然后那个儿子手伸的老长把我上面的位置也覆盖了
所以至少要加上某个儿子的dp[v][x-1]
你以为这就完了?你其他子树弃疗了?
所以我们考虑子树v是被硬点伸手的那个,那么他向上伸手长度是x-1,把向上伸改成向旁边伸,这样他只能伸出x-2
那么其他儿子的要求就是向下x-2层
相当于其他儿子的dp[p][K+x-2]求个和
当然,你需要有个基础认知就是x=K-x所以是dp[p][K+K-x-2]求个和
这个题就做完了qwq
T2
20pts:我们考虑线性均摊,就是可以做到查询O(n)插入O(1)的那种,这样插入1e7个也随便跑
70pts:树套树,线段树套平衡树,菜鸡题目没有区间第k大所以直接用set就好,而且手写您也过不了更多
100pts:谢谢来自uoj群jiangly


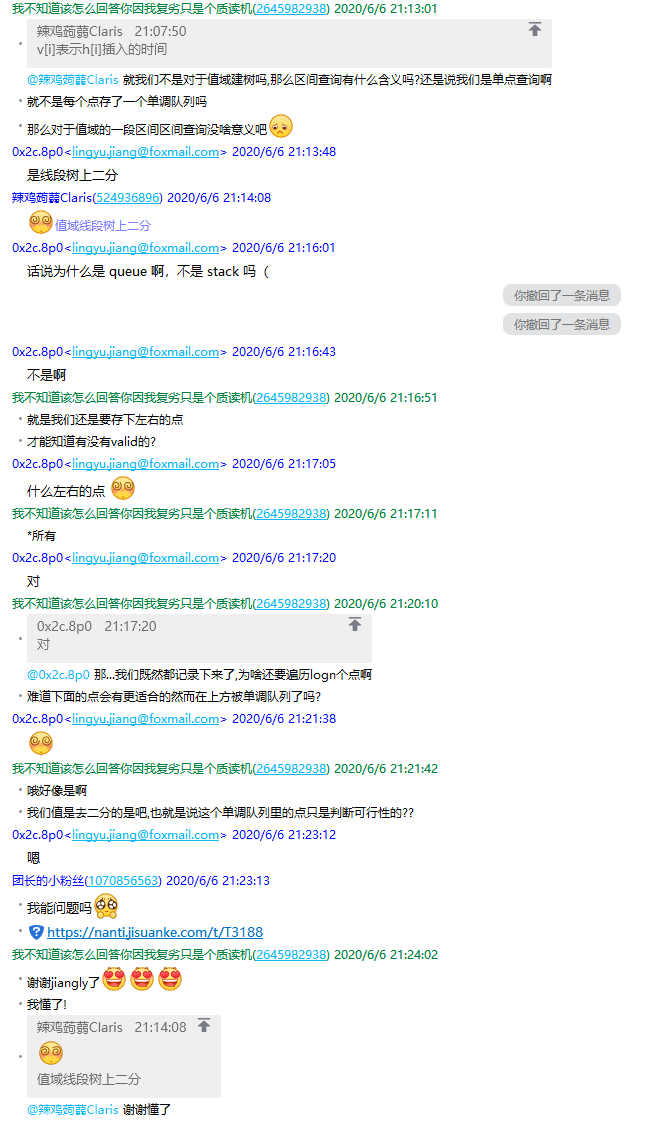
上面是更优做法,下面是官方标称
T2 逊!
倒着考虑:先插好所有元素,每次要不询问、要不删除一个元素。这种处理方式可以让我们事先在下标线段树里有序地预处理好每个节点范围内的数字(从底层一路归并上来,预处理复杂度只有一个)。
如何处理删除?因为我们使用线性存储,一个很自然的想法是并查集:设正反两个并查集,一开始都是指向自己的;每当一个元素被删掉后分别将它们指向前、后两个元素。 目前查询的效率是 的,因为我们要根据区间在线段树上找到 个节 点,每个节点二分出最接近的位置,再用并查集查询前后有效的元素。
有一个黑科技可以优化复杂度。对于线段树每个节点额外做一步预处理:对当前有序数组的每一个位置,维护它往左子树和右子树走下去对应的有序数组的下标(可以在归并的时候一并得到这些信息)。 这样每次询问时我们不必对 个节点一并二分,只需二分根节点的有序数组,其余的二分结果可以在遍历线段树时根据这些指针得到。
效率:
然后对于第三部分的解释:
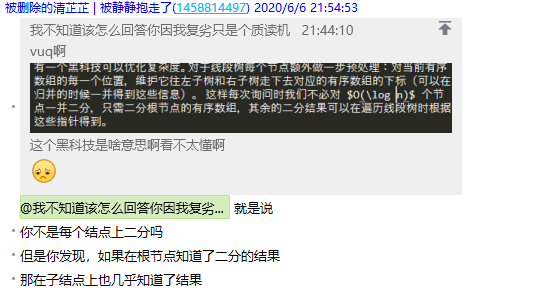

T3
40pts:您开开心心的设计出dp[i]表示前i张牌都打出去的最优收益,然后转移的区间众数可以预处理,然后O(n^2)的dp,并且看了一眼1.5次方使用了pow,然后您T了,连羽毛都腐烂在土地里面
52pts:预处理1.5次方
再往上?问zhq,orzhq
决策单调性优化,单调栈形式
难看的code:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using std::min;
#define ll long long
const int MAXN=5e5+7;
const int INF=1e9+7;
int ccnt,K,n;
int home[MAXN],nxt[MAXN],to[MAXN],fa[MAXN];
#define ad2(x,y) (ct(x,y),ct(y,x))
inline void ct(int x,int y) {
ccnt++;
nxt[ccnt]=home[x];
home[x]=ccnt;
to[ccnt]=y;
}
ll dp[MAXN][207],c[MAXN],siz[MAXN];
//从K+1到K+K是向下覆盖
//从K-1到0是向上覆盖
//K是刚好覆盖
inline void dfs(int u,int F) {
dp[u][0]=c[u];//向上k层
siz[u]=1;
for(int i=K+1; i<=K+K; ++i)dp[u][i]=0;
for(int i=home[u]; i; i=nxt[i]) {
int v=to[i];
if(v==F)continue;
dfs(v,u);
siz[u]+=siz[v];
dp[u][0]+=dp[v][K+K];
for(int j=K+1; j<=K+K; ++j) {
dp[u][j]+=dp[v][j-1];
}
}
if(siz[u]==1) { //叶子结点
for(int i=1; i<=K; ++i) {
dp[u][i]=c[u];//如果要想向上只能自己
}
} else {
for(int i=1; i<=K; ++i) {
dp[u][i]=INF;
}
ll rc[107];
for(int i=home[u]; i; i=nxt[i]) {
int v=to[i];
if(v==F)continue;
for(int i=0; i<K; ++i)rc[i]=dp[v][i];
for(int j=home[u]; j; j=nxt[j]) {
if(i==j)continue;
int p=to[j];
if(p==F)continue;
// printf("!%d\n",p);
for(int i=0; i<K; ++i)rc[i]+=dp[p][K+K-i-1];
}
for(int j=1; j<=K; ++j) {
dp[u][j]=min(rc[j-1],dp[u][j]);
}
}
}
for(int i=1; i<=K+K; ++i) {
dp[u][i]=min(dp[u][i],dp[u][i-1]);
}
return ;
}
int main() {
// freopen("test.in","r",stdin);
// freopen("T1_2.out","w",stdout);
scanf("%d%d",&n,&K);
for(int i=1; i<=n; ++i)scanf("%lld",&c[i]);
for(int i=1,x,y; i<n; ++i) {
scanf("%d%d",&x,&y);
ad2(x,y);
}
dfs(1,0);
// for(int i=1; i<=n; ++i) {
// printf("%d ",i);
// for(int k=0; k<=K+K; ++k) {
// printf("%d ",dp[i][k]);
// }
// puts("qwq");
// }
printf("%lld\n",dp[1][K]);
return 0;
}