夏晓光(loveJY)的博客

仍要向下扎根,向上结果

首页 归档 标签 关于 友链

「St-OI」Round2

2020-08-19 14 min read # 数据结构优化DP # 树上倍增 # 计数题 # 动态规划

T137862 「StOI-2」好多表达式

直接考虑算贡献,

首先看到第一档部分分不存在+,所以我们可以用一个dp来算一段的所有的乘积和....

然后仅存在一个+的时候,我们会发现,对于两段数,我们后面那一段的所有前缀会被额外统计一个前缀次

而前面那一段的所有后缀会被额外统计一个后缀个数次

所有也就是说对于一个* +的数(或者一段),他的(一段)统计次数很好算了

而对于+ num +这样的数,我们统计次数很好算是

  • num *这样的数会被dp算贡献了....

做完了

细节是注意整个序列乘起来的贡献还多出一部分

code:


#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int P = 998244353;
const int MAXN = 1e5 + 7;
int n, flg;
char s[MAXN];
ll a[MAXN], dp[MAXN], ans, b[MAXN];

inline void add(ll &x, ll y) {
	x += y;
	if(x >= P)x -= P;
}

inline void solve(int L, int R) {
	dp[L] = a[L];
	add(ans, dp[L]);
	for(int i = L + 1; i <= R; ++i) {
		dp[i] = (1ll * dp[i - 1] * a[i] % P + a[i]) % P;
		// printf("wan dan:%d?%d\n", i, dp[i]);
		add(ans, dp[i]);
	}
	ll tmp = 1;
	for(int i = L; i < R; ++i) {
		tmp = tmp * a[i] % P;
		add(ans, 1ll * tmp * (L - 1) % P);
	}
	tmp = 1;
	for(int i = R; i > L; --i) {
		tmp = tmp * a[i] % P;
		add(ans, 1ll * tmp * (n - R) % P);
	}
	tmp = tmp * a[L] % P;
	add(ans, 1ll * tmp * (L) % P * (n - R + 1) % P);
	add(ans, (P - tmp));
	return ;
}

int main() {
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i) {
		scanf("%lld", &a[i]);
		if(i != n) {
			scanf("%s", s);
			if(s[0] == '+')b[i] = 0;
			else b[i] = 1;
		}
	}
	for(int i = 1; i <= n; ++i) {
		if(b[i] == 0) {
			// printf("in + :%d %d\n", a[i], b[i]);
			if(flg == 0 && b[i - 1] == 0) {
				// printf("gongxian1 :%d %d %d\n", i, (n - i + 1), a[i]);
				add(ans, 1ll * a[i] * (i) % P * (n - i + 1) % P);
			} else if(flg) {
				// printf("qwq");
				solve(flg, i);//计算这一段乘的答案
				flg = 0;
			}
		} else if(flg == 0) {
			flg = i;
		}
	}
	printf("%lld\n", ans);
	return 0;
}

T137866 「StOI-2」简单的树

感觉60分随便做的样子

就是考虑记录每个点的一个最大值和次大值,然后对于改小或者改大都只是到根的一段路径权值变成他的次大值/a改后的值

然后直接树上倍增可以做到一个log qwq

但是接下来怎么搞啊??因为我们这样要做r-l+1次树上倍增啊.....

所以要推推式子啊....

首先对于只改大的情况:

l=ca,r>valil=c_a,r>val_i

那么贡献就是1+2+3....+(r−vali)1+2+3....+(r-val_i)

然后这个东西好像可以等差数列求和啊?

=(r−vali+1)(r−vali)/2=(r-val_i+1)(r-val_i)/2

然后这个东西好像可以拆开啊?

=(r2+vali2−2∗vali∗v+r−vali)/2=(r^2+val_i^2-2*val_i*v+r-val_i)/2

然后这个东西好像可以记录vali2val_i^2和valival_i然后O1求出一个点在r-l+1变化的贡献

然后树上前缀和一下再倍增一下好像就能OlogOlog了.....

对于只改小的情况

l=1,r<valil=1,r<val_i

我们已知有一段路径的答案是aia_i好像这一段的答案都会变成次大值或者最大值减少后的值....

考虑对于某一个内嵌三角形的矩阵求和?

首先可以把三角形上面的横长方形求和,出现次数就是最高的点最大值到次大值的差

然后再对于那些由次大值构成的近似三角形求个和,他们一定会出现r-l-sth次啊

然后再对于那些由r构成的斜三角形求和....可以用总的减去次大值构成的近似三角形的一部分算每一个的和....然后总的和近似三角形的和虽然都是变的,但是还是能求前缀和的吧?

其余情况我们一定能拆成这两种....

T131258 「StOI-2」不朽的逃亡者

数据结构优化DP?

dpi,j,kdp_{i,j,k}表示走到i,j后用了k个矩形

然后考虑但对于使用0~K个矩阵每行每列都建立一个优先队列,记录dp值与最远矩阵影响范围

对于每个矩阵建立两个minn数组,分别记录当前在矩阵下侧的圆圈格子...与右侧的圆圈格子的dp值中最小值

这个值与DP过程中分别在矩阵下侧时插入该列的优先队列与右侧时插入该行的优先队列

最远影响范围即矩阵上,左边界表示当前用了这个矩阵....

那么我们就可以得出转移方程

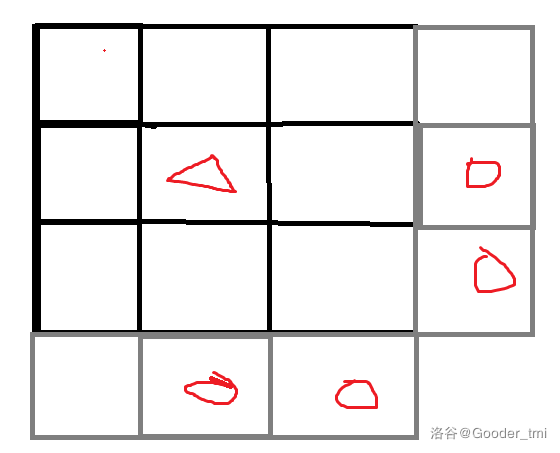
f[i][j][k]=a[i][j]+mn(f[i+1][j][k],f[i][j+1][k]);f[i][j][k]=a[i][j]+mn(f[i+1][j][k],f[i][j+1][k]);

f[i][j][k]=mn(f[i][j][k],mn(qx[i][k−1].top(),qy[j][k−1].top()));f[i][j][k]=mn(f[i][j][k],mn(qx[i][k-1].top(),qy[j][k-1].top()));

乱搞做法...

fi,j,k,lf_{i,j,k,l}当前在第i行第j列已经用了k个矩形现在第l个矩形最小价值

转移非常显然,套路前缀最小值套路滚动数组??

时间复杂度O(nmwk)O(nmwk)

这样有40ptsqwq

首先我们可以开O(nm)O(nm)个vectorvector然后存下每个格子上有哪些矩形可以优化很多

假设所有可用矩形面积和为sum,那么总时间复杂度是O(sum∗w)O(sum*w)

sum很大时数据随机意义下答案是0

所以一定有的格子没有用到,也就是说用到总矩形数很少适当降低w的值即可

然后调调参1e8/sum取min可控制复杂度

P6799 「StOI-2」独立集

最后一题了update in 2020/8/30

树上独立集计数,我们想想序列上的怎么做?

其实能看出就是我们考虑把所有的按照区间右端点排序,然后依次处理,fif_i表示处理前i个链的方案数

转移的时候如果我们不选直接+fi−1+f_{i-1}

否则我们找到LiL_i之前的最近的一个链的右端点RiR_i,fi+=Rif_i+=R_i

链上的就解决了

树上的,我们考虑fi,0/1f_{i,0/1}表示点i经过/没经过链的方案数

然后我们只选择LCA是i的所有链来转移fu,1f_{u,1}

先钦定gi=fi,0+fi,1g_i=f_{i,0}+f_{i,1}

转移方式:考虑这条链上其他所有的儿子节点的gig_i乘起来

相信我这个东西可以变成链上的信息

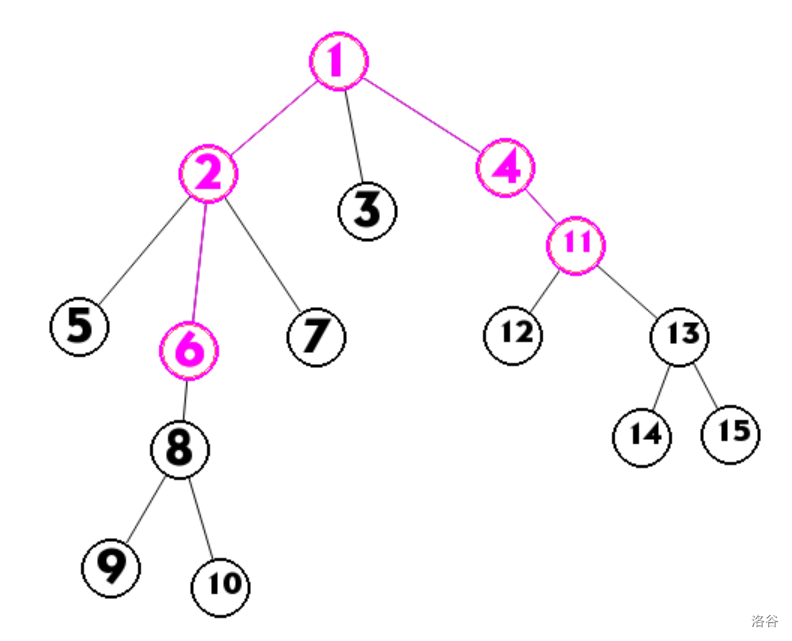
显然选上了这条链转移就是所有链上的点的非链上儿子的g的乘积

即$g_5 * g_7 * g_8 * g_3 * g_ 12 *g_13 $

这个东西显然不好优化,所以我们考虑把它们向链上靠

g12∗g13=f11,0g_ 12 *g_13 = f_{11,0}

g8=f6,0g_8 = f_{6,0}

g5∗g7=f2,0/g6g_5* g_7 = f_{2,0}/g_{6}

g3=f1,0/g2/g4g_3 = f_{1,0}/g_{2}/g_{4}

现在式子变成了

f11,0∗f6,0∗f2,0/g6∗f1,0/g2/g4f_{11,0}*f_{6,0}* f_{2,0}/g_{6}* f_{1,0}/g_{2}/g_{4}

g,f分开f11,0∗f6,0∗f2,0∗f1,0/g2/g4/g6f_{11,0}*f_{6,0}* f_{2,0}* f_{1,0}/g_{2}/g_{4}/g_{6}

你发现好像有的点没有*f/g,比如f4,0f_{4,0},g11g_{11}

唉?但是两个好像是相等的?所以可以直接加上去?所以就等于

f11,0∗f6,0∗f2,0∗f1,0∗f4,0/g2/g4/g6/g11f_{11,0}*f_{6,0}* f_{2,0}* f_{1,0}*f_{4,0}/g_{2}/g_{4}/g_{6}/g_{11}

所以这些其他点的g乘起来可以变成链上所有点f0f_0乘起来除以除了LCA外所有的gg,

这样我们就能直接树链剖分维护了QAQ....

一看数据范围5e5过不了啊

但是这个链查询能离线

所以可以变成子树乘和树上差分用树状数组维护一下就做完了

细节注意下LCA的f0f_0可能会被算两遍....

code:


#include<bits/stdc++.h>
using namespace std;
const int P = 998244353;
#define ll long long
const int MAXN = 5e5 + 7;
const int MAXM = 1e6 + 7;
vector<int> v[MAXN];
int n, m, ccnt;
int home[MAXN], nxt[MAXM], to[MAXM];
ll f[MAXN][2], g[MAXN];
struct rec {
	int x, y;
} e[MAXN];

inline void ct(int x, int y) {
	ccnt++;
	nxt[ccnt] = home[x];
	home[x] = ccnt;
	to[ccnt] = y;
}

int siz[MAXN], son[MAXN], fa[MAXN], dep[MAXN], dfn[MAXN], depp;
inline void dfs1(int u, int F) {
	siz[u] = 1;
	dfn[u] = ++depp;
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v == F)continue;
		fa[v] = u;
		dep[v] = dep[u] + 1;
		dfs1(v, u);
		siz[u] += siz[v];
		if(siz[v] > siz[son[u]]) {
			son[u] = v;
		}
	}
	return ;
}
int top[MAXN];
inline void dfs2(int u, int topf) {
	top[u] = topf;
	if(!son[u])return;
	dfs2(son[u], topf);
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v == fa[u] || v == son[u])continue;
		dfs2(v, v);
	}
}

inline int LCA(int x, int y) {
	while(top[x] != top[y]) {
		if(dep[top[x]] < dep[top[y]])swap(x, y);
		x = fa[top[x]];
	}
	if(dep[x] > dep[y])swap(x, y);
	return x;
}

inline ll add(ll &x, ll y) {
	x += y;
	if(x > P)x -= P;
	return x;
}

inline ll mul(ll &x, ll y) {
	x = x * y % P;
	return x;
}

namespace BIT {
	ll tr[MAXM];
#define lowbit(x) (x&(-x))
	inline void init() {
		for(int i = 1; i <= n; ++i)tr[i] = 1;
	}
	inline void mdf(int x, ll y) {
		for(; x <= n; x += lowbit(x))mul(tr[x], y);
	}
	inline ll query(int x) {
		ll ret = 1;
		for(; x; x -= lowbit(x))mul(ret, tr[x]);
		return ret;
	}
}
using namespace  BIT;

inline ll ksm(ll x, ll y) {
	if(x == 1)return 1;
	ll ans = 1;
	while(y) {
		if(y & 1)
			ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

inline void dfs3(int u, int F) {
	f[u][0] = 1;
	for(int i = home[u]; i; i = nxt[i]) {
		int v = to[i];
		if(v == F)continue;
		dfs3(v, u);
		mul(f[u][0], g[v]);
	}
	f[u][1] = 0;
	for(int j = 0; j < (int) v[u].size(); ++j) {
		int L = e[v[u][j]].x, R = e[v[u][j]].y;
		add(f[u][1], query(dfn[L]) * query(dfn[R]) % P * f[u][0] % P);
	}
	g[u] = f[u][1] + f[u][0];
	mdf(dfn[u], f[u][0]);
	mdf(dfn[u] + siz[u], ksm(f[u][0], P - 2));
	mdf(dfn[u], ksm(g[u], P - 2));
	mdf(dfn[u] + siz[u], g[u]);
	return;
}


int main() {
	scanf("%d%d", &n, &m);
	for(int i = 1, u, v; i < n; ++i) {
		scanf("%d%d", &u, &v);
		ct(u, v);
		ct(v, u);
	}
	dep[1] = 1;
	dfs1(1, 0);
	dfs2(1, 1);
	for(int i = 1; i <= m; ++i) {
		scanf("%d%d", &e[i].x, &e[i].y);
		int anc = LCA(e[i].x, e[i].y);
		v[anc].push_back(i);//加入这条链...
	}
	init();
	dfs3(1, 0);
	printf("%lld\n", g[1]);
	return 0;
}
Powered by Gridea RSS