夏晓光(loveJY)的博客

随机算法

马尔科夫不等式

一个随机变量x,大于他的期望的k倍的概率小于等于$1/k$

$Pr[x\geq kE[x]]<=1/k$

条件概率

$Pr[A|B]=Pr[A ∪ B]/Pr[B]$

独立事件独立随机变量qwq

LasVegas随机算法

正确随机算法

MonteCarlo随机算法

不一定正确

随机快排

随机找出一个元素,把小于他的分为A,大于他的分为B,等于他的设为C

然后递归A,B部分继续排序

分析复杂度可以考虑数学归纳,利用期望时间

T(n)为n个元素排好序的期望时间

于是我们有$T(n)=O(n)+\sum_{i=0}^{n-1}T(i)T(n-1-i)$

后面那个式子的取值显然就是

$T(n)=O(n)+\frac{2}{n}\sum T(i)$

然后后式是有限微积分,其实就是

$\frac{2}{n}\sum i \ln i$

然后$ln x$积分是$x\ln x$

就整完了

$T(n)=O(n)+O(n\ln n)$

随机选择找第k大算法复杂度分析

$T(n)=\frac{1}{n}(T(n-1)+T(n-2)+T(n-3).....+T(n/2)+T(n/2)+T(n/2+1)...T(n))$

于是归纳一下,假设这个东西成立$T(n-1)<=cn$

$T(n)<=\frac{2c}{n}\frac{(n/2+n-1)(n/2)}{2}+tn$

化简这个式子,最后保证$c\geq tn$即可

咕了

然后讲到哈希的时候回来了

$k<2^n$

n不太小,整除k的不同素数个数小于$pai(n)$

然后我们对于字符串哈希,有出错概率为$O(\frac{1}{p})$

因为相当于我们要构造两个串,满足哈希值之差被p整除,而且位数相同

那么有他们的差是p的倍数

咕了

下午

IOI2020D2T2数蘑菇

做法这不显然嘛,O(n)枚举询问!

一看

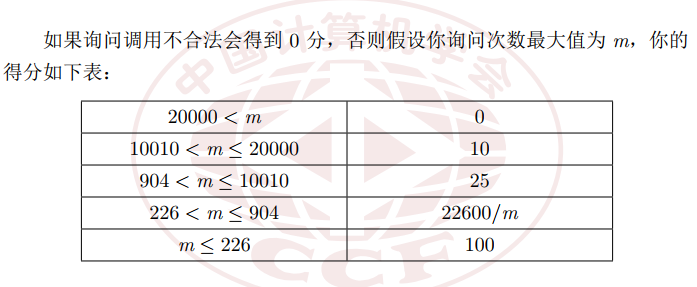
我擦,226次,这么少?还是卡常题?

考虑基本算法1,我们大小分块,首先用$O(2*B)$询问问出一个大小至少为$B$的块,然后利用这样的询问:

$0 x_1 0 x_1 0.....$

0只是代表他们属于A

进而得到一个段中有多少个属于$A$

最优$2.82\sqrt n$

卡常1

我们发现根据最后一个元素的奇偶性可以得知最后一个元素的类型

即$0,x_1,0,x_2,0...x_n$

假设我们现在使用的B都是A元素,那么最后一个的信息可以直接知道是什么集合

你又发现了,如果我们每次找到属于类的新元素使得已知信息的块长变大了,我们可以使用属于A/属于B中较大的那个块,继续询问未知

这样是$2\sqrt n$

卡常2

有一个很牛逼的操作是

$0 x_1 0 x_2$

简单分类讨论可以知道两个元素的类型

这样节省了一开始的操作

$1.75\sqrt n$

最后的优化

我们有一个神仙构造方法

考虑如果能询问一个集合中的元素和,然后最少多少次询问出整个集合的每个元素的和呢

有一个合并构造的方式

比如我们有a次询问大小为b的$B1$解决了

然后另外也有一个大小为b的$B2$被a次解决了

那么两次询问的第i次操作的集合$S1,S2$拿出来

我们额外询问一次$B2$的和,然后再每次询问$S1+S2,S1+B2/S2$的和

相加我们就能得到$S1$的和

然后对应到本题,你发现$S1$的奇偶性,能够帮助我们回答最后一个元素的取值,所以我们可以在S1后面接一个x,就是额外确定了一个元素x

那么我们就做到用$2n+1$知道$3n$个元素了

再加上我们有两个集合拼起来后,末尾的一个0,总共就有$5n+1$个元素了

这道题就做完了

这是个什么题啊?

状压点u相邻10个点所有点能不能放区间端点即可

$i^2$ 的增长速度是单调上升的

所以我们画出图,就是利用元素x凑出一个固定体积的代价,一定是代价先下降,然后再上升的,而且这个图像是凸的,就是他的$f_{i+2}-f_{i+1} > f_{i+1}-f_{i}$

如果我们能,一定会选性价比最高的那个,就是$\frac{i^2+C}{i}$值最小那个

然后我们就能知道,每个背包一定是在一个小范围内暴力,然后范围扩大之后是选取一个固定大小的物品知道小范围内

任何完全背包其实也是这样的,但是完全背包理论上界是$v^2$之后才会,但是这道题因为其性质是$O(C)$

这里选取3C,然后你发现背包卷积的时候,我们只会有O(\sqrtC)种物品可以用来卷积啊

我也不知道为啥啊,好像个数超过就可以减少

因此

考虑对于一个给定的石柱$(x,y)$计算什么时候会崩塌

如果有一个空柱子$(x',y')$那么就会在$|x-x'|+|y-y'|$时间后崩塌

然后设第i组的答案为$ans_i$

我们显然有不等式$ans_i-1\leq ans_{i+1} \leq ans_{i}+1$

根据这个式子我们可以知道对于一个现在还存在的石柱子,他的存活区间左右端点是单调变化的

然后设$(i,l_i-1),(i,r_i+1)$为上下关键点,不难发现就可以代表所有信息,于是我们既有左右侧上下关键点的单调队列

就是维护一个菱形阶梯状空白点的单调队列,他们记录的是到达某一个点的信息

然后我们考虑从i变到i+1,对于右边的,相当于删掉一些空白点,然后右端点还可以向右移动加入新的更多关键位置

左端点就相当于左边界向后移,然后加入新的右边界

直接维护四个单调队列即可,然后对于i号位置的答案的查询相当于四个单调队列中最小值的查询

不难发现这个拿菜的顺序不应该有包含,应该是都相交,因为我们要让所有人拿饭最大值最小啊

然后你就会发现,在这上面匹配的顺序应该是类似于双指针的过程,一个个跳

然后就变成一个b的循环移位和a匹配了

有这个我们就能做呢,考虑枚举一个循环移位,然后我们有每个位置直接顺时针匹配的答案,不难发现我们要最小化几个顺时针匹配的答案,就是考虑所有顺时针匹配的最慢的几个人逆时针匹配

按照时间排序,枚举这个分界点即可,相当于先让他们逆时针了,然后再根据这个形态顺时针匹配

考虑一个合法的路径形态一定是走到一个异色奇环上

也就是说我们要找一个异色的奇环,而且要保证从1能够走异色边走过去

就保留所有异色边,然后如果存在一条$1->u->v$简单路径,而且$u->v$存在同色边就能成为答案了

于是建立圆方树,如果存在$1->u->v$的简单路径,当且仅当在圆方树上存在简单路径

那么要么是在某一个点的子树内,要么u的父亲方点代表子树中包括v

中间值一定最优By dmy

我不会啊

不难发现答案是一个关于t的二次多项式

然后我们就有

对于树上每个节点维护这个系数答案即可

长度为$[a,b]$

考虑连通块满足某个区间编号信息怎么做?

简单扫描线,计算左端点固定的时候子图的点数-边数值,满足是连通块的会有这个值为1,用线段树维护即可

然后你发现我们现在是树链

考虑树链一定是满足虚树为一条链,同时是连通块

那么你就会发现这样的可以直接做呢!就是维护极大虚树为链的区间,然后直接算这里面有多少是连通块即可

仔细思考,我们不可能有点数减边数小于1的,所以还是直接维护区间最小值及其个数即可