小粉兔的圆方树

圆方树基础入门讲解

圆方树是解决仙人掌问题的利器!

点双连通分量:任意两点间都至少有两条点不重复的路径的极大子图

这个不重复既指简单路径,也指两点间其他路径

这个定义基本等价于没有割点的图,当且仅当两个点一条边的时候失效

和边双连通分量正好相反的是,每个边只能属于一个点双,但是每个点可能属于多个(割点)

在圆方树中,每个方点代表一个原图点双分量,一个原点是一个正常的点qwq

每个点双对应的方点向这个点双的每个点连边qwq

这样每个点双形成一个"菊花图"

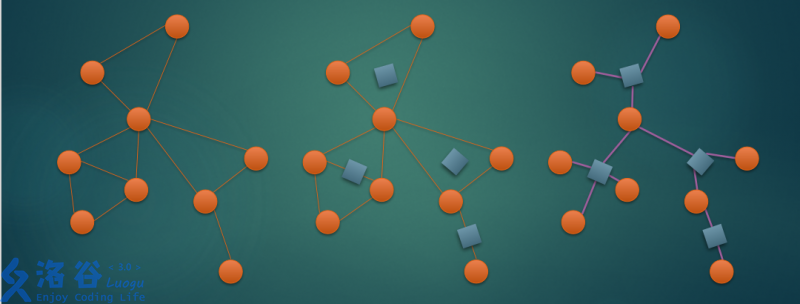
圆方树的点数小于2n,所以数组要开4倍

同时注意可能形成森林,即原图不连通

引入tarjan算法,就是求强联通分量的写法:定义 $dfn_x$ 为xdfs序, $low_u$ 为u走至多一条返祖边或横跨边能够到达的最小dfn序

我们考虑在一个点双的深度最浅处确定整个点双,假设那个点是u

那么对于v为u的儿子,且刚好是走树边到达的,一定都有 $low_v==dfn_u$

否则v就能走树边/返祖边到达更浅的节点,与u的定义冲突

找到这个点双后,我们像缩点一样不断的弹出栈直到点u,来得到整个点双的信息

同时建立一个方点,把他和点双连边即可

方点编号从n+1开始,这样更为方便

code:

#include <cstdio>
#include <vector>
#include <algorithm>

const int MN = 100005;

int N, M, cnt;
std::vector<int> G[MN], T[MN * 2];

int dfn[MN], low[MN], dfc;
int stk[MN], tp;

void Tarjan(int u) {
    printf("  Enter : #%d\n", u);
    low[u] = dfn[u] = ++dfc; // low 初始化为当前节点 dfn
    stk[++tp] = u; // 加入栈中
    for (auto v : G[u]) { // 遍历 u 的相邻节点
        if (!dfn[v]) { // 如果未访问过
            Tarjan(v); // 递归
            low[u] = std::min(low[u], low[v]); // 未访问的和 low 取 min
            if (low[v] == dfn[u]) { // 标志着找到一个以 u 为根的点双连通分量
                ++cnt; // 增加方点个数
                printf("  Found a New BCC #%d.\n", cnt - N);
                // 将点双中除了 u 的点退栈，并在圆方树中连边
                for (int x = 0; x != v; --tp) {
                    x = stk[tp];
                    T[cnt].push_back(x);
                    T[x].push_back(cnt);
                    printf("    BCC #%d has vertex #%d\n", cnt - N, x);
                }
                // 注意 u 自身也要连边（但不退栈）
                T[cnt].push_back(u);
                T[u].push_back(cnt);
                printf("    BCC #%d has vertex #%d\n", cnt - N, u);
            }
        }
        else low[u] = std::min(low[u], dfn[v]); // 已访问的和 dfn 取 min
    }
    printf("  Exit : #%d : low = %d\n", u, low[u]);
    printf("  Stack:\n    ");
    for (int i = 1; i <= tp; ++i) printf("%d, ", stk[i]);
    puts("");
}

int main() {
    scanf("%d%d", &N, &M);
    cnt = N; // 点双 / 方点标号从 N 开始
    for (int i = 1; i <= M; ++i) {
        int u, v;
        scanf("%d%d", &u, &v);
        G[u].push_back(v); // 加双向边
        G[v].push_back(u);
    }
    // 处理非连通图
    for (int u = 1; u <= N; ++u)
        if (!dfn[u]) Tarjan(u), --tp;
        // 注意到退出 Tarjan 时栈中还有一个元素即根，将其退栈
    return 0;
}

夏晓光(loveJY)的博客

ytez省队集训讲课篇二轮