可怜的后缀自动姬啊

连全尸都么得啦/ll

问题引入

给定一个 01 串 S，记它长度为 i 的后缀为 $S_i$，我们把总共 $n$ 个 $S_i$ 都插入到一棵字典树中，并且把每个 $S_i$ 最后一个字符对应的节点涂黑，剩下的节点都是白色，不难发现总共会涂黑恰好 $n$ 个节点。

之后，我们把所有度数不为 $2$ 的节点都涂黑（指把儿子个数不为 $1$ 的节点都涂黑），特别的，也涂黑根节点。我们选出所有的黑色点对 $i,j$（需要满足 $i$ 的深度不超过 $j$ 的深度），且 $i$ 到 $j$ 的路径上不经过其它黑色点，把 $i$ 到 $j$ 路径上的字符连起来形成一个字符串，并且把这个字符串的本质不同子串数累加进答案。

你需要输出这个答案。

怎么$O(n^2)$?

按照题目所说建立后缀字典树,然后在树上dfs,每次dfs向下走的时候将字符插入sam中,然后我们dfs到一个黑色节点就统计答案并清空sam

怎么$O(nlog^2n)$?

建立完备后缀树,即后缀字典树的完全最小化结果

对于在后缀树上的点$u$和点$f_u$,他们之间记录了$pos_i-len_i$到$pos_i-len_{fa_u}+1$这一段反串上的子串,$pos_i$是儿子节点中深度最大节点

于是我们可以知道询问总数只有$O(n)$,组,同时询问类型为区间本质不同的子串数,LCT+segment tree维护即可

怎么$O(n)$?

wc

后缀自动机与后缀树

后缀字典树是一颗$O(n^2)$级别的树,储存了所有后缀信息,是DFA(确定性有限状态决策自动机)

DFA与NFA的区别在于决策是否提前固定,换句话说,将所有可能的字符串预处理出来,就都是DFA

DFA存在最小化概念,即改造为等价且拥有最少状态的DFA的过程

后缀自动机,则是将所有right集合相同的节点压缩为1一个节点,则可以认为这些节点是等价的

含有性质

\forall node~u,v,right(u)\subset right(v)/right(u) \and right(v) = \empty

读者自证不难

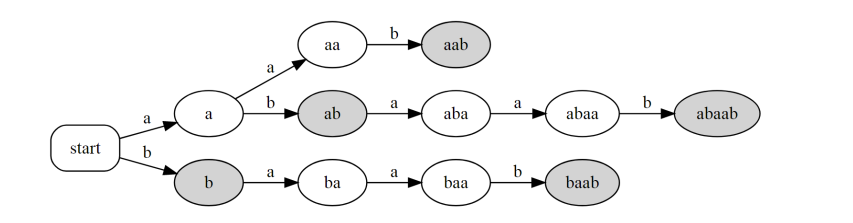
对于abaab字符串构建后缀字典树/自动机

最小化后缀字典树

我们发现对于后缀集合只差$|S|$这一个元素的$right$集合,他们会发现的后续转移还是一样的,因此可以合并

相反,如果right集合对称差不仅仅差了$|S|$这个元素,他们的后续转移就是不同的,我们不能够将他们合并

因此最小化后缀字典树和后缀自动机的唯一区别在于是否将right集合对称差仅为$\{|S|\}$的节点合并

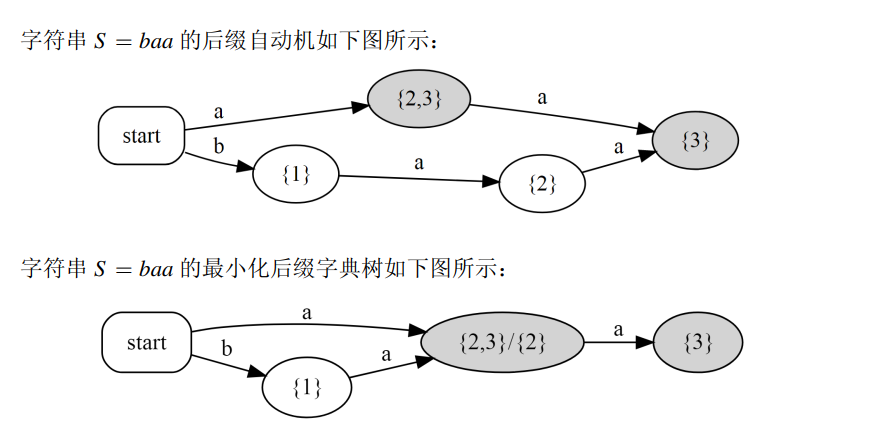
同时不难发现,沿着SAM的边进行DFS,就能够还原原来的后缀字典树

后缀字典树的收缩,则是将所有叶子节点单独提出,构建虚树,得到的虚树则称为后缀树

然额,这样建立的后缀树可能不包含一些后缀节点,因此我们再包含所有后缀节点的情况下建立的虚树,成为完整后缀树,也是我们平常使用的后缀树

压缩后缀自动机

对后缀树进行最小化操作,或者对后缀自动机进行收缩,得到的结构则是压缩后缀自动机

不难发现我们向后顺序无关,因此一般同时进行两个操作进行压缩

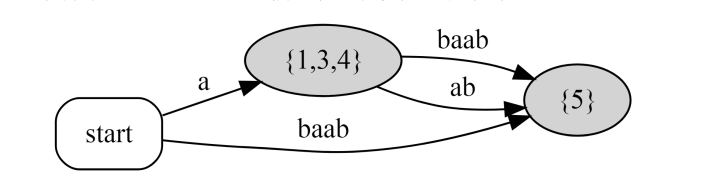
字符串abaab的压缩后缀自动机

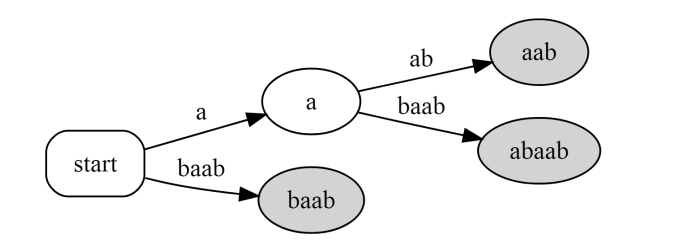
将abaab,aab,baab节点合并得到$\{5\}$节点,然后单独a节点形成$\{1\}\{3\}\{4\}$

压缩出度为1的所有节点$\{2,5\},\{3\},\{4\}$,把他们直接并入$\{5\}$

不难发现我们舍弃了很多后缀节点,因此对完整后缀字典树进行最小化操作,得到的节点为完整后缀自动机

构造压缩后缀自动机算法

建立后缀自动机,按照拓扑序处理,对于出度为1的点,找到他指向的节点合并到的节点,即一个出度不为1的灰色节点

同时对于指向他的出边压缩给合并进入的节点

最后构造得到的即为后缀自动机

如何构建完整压缩后缀自动机?

将后缀自动机上所有right集合包含n的节点同样染灰色

再次收缩即可

不难发现,以上过程时空复杂度均为O(|S|)

性质与应用

性质1

各个节点在压缩后缀自动机上的所有入边上的字符串是其中最长者的后缀

性质2

在压缩后缀自动机上 DFS ，可以还原出后缀树

分别对应压缩后缀自动机是后缀树的最小化结果和后缀自动机的收缩结果

性质3

$L_i$为压缩后缀自动机第i个节点所有出边最长边的长度

那么我们有$\sum L_i=O(|S|)$

证明:

考虑后缀自动机收缩过程,每收缩一条边

(1) 出现在灰色节点最长边上

$L_i+1$

(2) 没有出现在最长边上

$L_i$不变

因为收缩边数$O(|S|)$,因此$\sum L_i=O(|S|)$

solution

建立压缩后缀自动机

根据性质2对于每个自动机上每条出边,都对应后缀树上的一条或者多条边

如果我们能求出压缩后缀自动机上每条边的答案,就能知道对应后缀树上每条边的答案

而这些出边形成的字符串,根据性质1,都是最长字符串的后缀

因此,我们每次在压缩后缀自动机节点上建立sam向前扩展,并同时记录所有边对应的答案,就可以得到后缀树上所有的答案了

该算法复杂度为$O(\sum L_i)=O(|S|)$

于是我们最终得到了一个线性复杂度的算法

本题的实际实现不需要建立该自动机,只需要隐式的表示出所有边然后直接回答即可

Finished!