qwqchang负责内容:

网络流!

互不相交最短路最大数量

把所有可能成为最短路的边拿出来, $dis_u-dis_v=w_e$ ,建图跑最大流

互不相交的最长LIS计数

$dp_j$ 表示j结尾的最长LIS长度

源点向所有为1的连边,汇点向所有最大的 $dp$ 数组连边

然后 $dp_j$ 向 $i<j,dp_i=dp_j-1$ 的i连边

跑网络流即可,和上个题相似

POJ3680

若干个区间 $[a_i,b_i,c_i]$ 代表把 $(a_i,b_i)$ 覆盖一次得到 $c_i$ 权重,问1~n所有点被覆盖不超过k次的最大权重

点转边是总没问题,不过这个是开区间,没意思,

$a_i$ 向 $b_i$ 连出一个权值为 $c_i$

此时从 $a_i->b_i$ 是限制他覆盖的中间点

跑最大费用最大流

(好像被李队卡了)

拆点限制流量,就能做闭区间了,但是不需要,我们好像直接扩展一下就好了

费用流

Dijkstra做法:每个点加上一个势能函数

inline void Dijkstra(){
	max_flow=0;min_cost=0;
	while(1){
		memset(dis,0x3f3f3f3f,sizeof(dis));
		while(!heap.empty())heap.pop();
		dis[s]=0;
		heap.push(make_pair(0,s));
		while(!heap.empty()){
			int u=heap.top().second;
			int tmp=heap.top().first;
			heap.pop();
			if(tmp!=dis[u])continue;
			if(u==t)break;
			for(int i=home[u];~i;i=next[i]){
				int v=to[i];
				int nowc=w[i]+h[u]-h[v];
				if(f[i]>0&&dis[v]>dis[u]+nowc){
					dis[v]=dis[u]+nowc;
					heap.push(make_pair(dis[v],v));
					prep[v]=u;
					pred[v]=i;
				}
			}
		}
		if(dis[t]>inf)break;
		int nowflow=inf;
		for(int i=1;i<=n;i++){
			h[i]+=dis[i];
		}
		for(int i=t;i!=s;i=prep[i]){
			nowflow=min(nowflow,f[pred[i]]);
		}
		for(int i=t;i!=s;i=prep[i]){
			f[pred[i]]-=nowflow;
			f[pred[i]^1]+=nowflow;
		}
		max_flow+=nowflow;
		min_cost+=nowflow*h[t];
	}
}

注意这个是没有负权边的,如果有负权边要先跑spfa求出最短路求出这个势能函数h

然后再去跑

P5295 [北京省选集训2019]图的难题

脑补结论?

至少要满足:

$E<=2V-2$

同时要满足任意一个导出子图,都要满足这个条件

充分性:你一定可以构造一个合法的方案,满足所有子图都是合法的,你会发现假如原来为 $2v-x$ 个边,然后这个点加入会有至多x个边代价,但是原图会有x个树,加入的时候可以以每个树都分配一个颜色

同时如果有多个可以划分为若干个子图,然后每一个都达到2v-2的那些,我们可以把每个连通块内的连接同色树的用两个颜色分开,并且和其他的连通

必要性:即本题猜出结论的方式:两颗生成树是上界,超过这个生成树就完了

$E-2V<=-2$

最大权闭合子图即可QAQ

这个建模就是S向所有的负权点连出负负权的边

然后 $E \in (u,v)$ 从 $E$ 向 $u,v$ 连边inf流量,然后从 $u,v$ 向 $T$ 连边流量1即可

最大密度子图

二分答案

$\frac{E}{V}$ 最大

二分答案k有

$E-kV>=0$

跑最大权闭合子图即可

HDU3605

n个人去m个星球,每个只能去固定的那些,一个星球最多容纳 $k_i$ ,问每个人只能去给定的若干个中的一个

$m=10,n<=1e6$

$2^m$ 枚举一个集合然后把这个集合的权算出来然后就做完了

直接左侧 $2^m$ 右侧为m个点即可

HDU3338

外层图形是凸的

每个黑块右上角有数字就是行的和,列有数字表示这一列的和为某个值

问这个数组的数独有没有解

上下界QAQ?

你发现限制都是 $[1,9]$ ,所以可以每个都流一遍变成 $[0,8]$

然后就有行点列模型

每一行变成一个点,每一列变成一个点,然后行和列之间连边为x,有[0,8]限制,表示这行和这列的交点为某个流量

然后跑一个最大流,因为一定满流

然后中间的边流量就是对应点写的数字-1

HDU3472

有n个单词,你可以把每个单词首尾连接起来

当且仅当两个单词首尾单词相同

告诉你一些单词可以翻转

问能不能

$n<=1000,T<=50$

混合图欧拉路

哈密顿路是NPC

现在我们转成求一个图的欧拉路,但是这个边会完蛋qaq

首先判断连通性!!欧拉回路:

无向图每个点都是偶数

有向图每个点入度等于出度

欧拉路:

无向图至多两个为奇数

有向图至多两个不满足一个in-out=1一个out-in=1

有向图回路:任意钦定方向

如果只有 $in-out\%2=1$ 完蛋了,不可能平衡

定义每个点度数差的绝对值为 $2x$

考虑调整使得 $x=0!$

原图有向边不变

钦定的无向边怎么钦定怎么连

流过一个流就是反向这个边

对于u->v任意一条路径流过去后起点 $in++,out--$ ,终点 $out++,in--$

中间的点没变

当出度大于入度就S向它连一个,流量为x

当入度大于出度的点就向T连边,流量为x

如果存在最大流就完了

现在还是欧拉回路QAQ

做法1:暴力枚举一个边 $(i,j)$ 加入qaq,每次暴力跑欧拉路

做法2:你会发现有两个点度数是奇数

我们搞一个无向边就好了

然后跑欧拉回路上述问题

然后删掉这个边跑欧拉路问题

HDU4067

考虑钦点每个边先选择这个代价小的,然后问题变成我们可能反向一个边,问凑成欧拉路最小代价

$(u,v),a<=b,in[v]++,out[u]++$ 连接 $[v,u,1,b-a]$

$(u,v),a>b,[u,v,1,a-b]$

你考虑一个路径 $u->v$ 流过去

相当于反向删除正向点亮QAQ

此时还是欧拉路,我们转换成欧拉回路

正着看u的out++,v的in--所以我们是u连接s,v连接t

负边权最短路,线性规划??

P3980 [NOI2008] 志愿者招募

一面对多面,一个选了对于多个都有影响

考虑在一面上下功夫,没有一个人流量为1

我们人为钦定这个流量为inf,然后从每个点流一个 $s_i,s_i+1$ 一个 $inf-a_i$

也就是说钦定每个点至少有 $a_i$ 的跨越度

设 $x_i$ 表示需要的第i类志愿者数量,然后 $a_{i,j}$ 表示第i天第j类志愿者能否工作

$\sum a_{i,j}x_j>=A_i$

限制条件, $\forall x_j,x_j \in {0,1}$

$\min \sum C_ix_i$

这个怎么做呢?

首先看样例 $x_1>=2,x_1+x_2>=3,x_3>=4$

设 $y_i$ 为多召唤了多少人

有等式:

$0=0$

$x_1-y-1=2$

$x_1+x_2-y_2=3$

$x_3-y_3=4$

$0=0$

然后我们每个用上面减去下面

那么我们总有每个变量出现两次且仅出现两次

一正一负

因为x是连续的,而y每个方程组仅有一个

移项后

$2-x_1+y_1=0$

$1-x_2-y_1+y_2=0$

$1+x_1+x_2-x_3-y_2+y_3=0$

$-4+x_3-y_3=0$

每个方程看成一个点,然后正入负出

-4向T连边流量为4

211向S连边流量为211

只看y,一个单独的y

负的向正的连 $inf,0$

比如点2向点1连边

然后我们考虑 $x_i$

此时和 $y$ 的一样,但是要带上费用,流量都是 $inf$

HDU

有一个河道,内向树,然后每条边有个污染的权值 $u_i$

有一个入海口和若干个出开口

有m份药剂,对于连续的一段河道(从儿子到祖先路径), $[x,y]$ 的污染值下降1

然后药剂有一个 $c_i$ 元而且最多 $k_i$ 瓶

怎么在最小花费的case下然后 $u_i$ 都是0

儿子向父亲差分即可

对偶

P3305 [SDOI2013]费用流

实数域二分答案

然后问题变成边有个额外的限制能不能在这个限制下跑到最大流

就做完了

注意合并重边这题边太多了!

F=\sum_{i=1}^na_ix_i+\sum_{i=1}^n(1-x_i)b_i+\sum_{i=1}^n\sum_{j=i+1}^nx_i*(1-x_j)c_{i,j}

选或不选的一个贡献

a选b不选的一种类型

S向所有点连 $b_i$ , $a_i$ 向T连边,然后考虑第三类是 $i->j$ 号点连 $c_{i,j}$

HDU4307

$D=(A*B-C)*A_T$

其中 $A_T$ 是转置矩阵,就是交换行和列后的A

会变成 $\sum x_i\sum x_jB_{j,i}-\sum x_ic_i$

$a_ia_j=1-(1-a_ia_j)$

$\sum_i\sum_jB_{i,j}-\sum_{i}\sum_{j}(1-a_ia_j)b_{j,i}+\sum_{i=1}^na_ic_i$

$1-a_ia_j$ 相当于与非

与非是 $!(x\&y)$

枚举与非的case,可以变成 $[a_i=0]+[a_i==1\&\&a_j=0]$

不选取为 $b_{j,i}$

选取为 $c_i$

一个选一个不选为 $b_{j,i}$

就变成了上面的模型

注意是不选方的点向选方的点连边,相当于要促进割掉选方不选边和不选方选边

P2050 [NOI2012] 美食节

每个人拆出p个点,你TLE了/cy

就是考虑第j个厨师的第w层表示第w个菜倒着做了哪个?

于是我们拆点后两边 $t_{i,j}*w$

这样点数太多了

所以我们考虑动态加点,每次在残量网络上跑网络流,就是对的!

SGU438

题目大概说有m个人要过一条宽W的河，人最远跳远距离是d，河上有n个垃圾堆，每个垃圾堆都有坐标和同一时间能容纳的人数，问所有人最少要跳几次才能跳到对岸。

qc:只能容纳一个人

每个石头拆成 $(i,t)$

你会发现能过河最慢时间是 $N+M$

那么我们总可以 $(i,t)$ 向 $(j,t+1)$ 连边,源点能跳到也连边

然后有容量限制可以拆点

枚举时刻在残量网络上流即可

POJ2175

满流最优的费用流一定没有负环,这是充要条件

所以我们找出给定的方案的负环然后dfs在这个继续增广即可

HDU3820

金蛋放在一个格子上有a

银蛋放在一个格子上有b

金蛋银蛋相邻损失c,d

两个格不一样

相邻要二分图染色!

选或者不选,同时选或者同时不选?

对于x步的点左金右银,对于y步的点左银右金

然后对应连边就好了!两侧金连边,两侧银连边,一个点向另一侧的连边

HDU2485

  2 题意：军队坐$bus$去机场 n个节点$(bus)m$条公交通路（单向）
  3 每走一条路花时间$1$问最少破坏几个结点（是相关联的的路都不能走)
  4 使军队在至少$k$时间不能到达机场。

路径长度大于k?

小于等于k的路径不合法?

我们考虑费用流!

S向起点连边,终点向T连边

然后拆点,i向i+n连边(1,0)

然后原图中一条边连接 $(u+n,v)$

于是你会发现这样就做完了

当我们费用大于k的时候停止即可

HDU3081

HDU2435

HDU4322

HDU3987

SPOJ859

szhlg负责内容:

P4262 [Code+#3]白金元首与莫斯科

本题状态设计很毒瘤啊

首先两次简单插头dp,算出从上到下从下到上的dp信息,并且处理成可以合并的形式

我们只用01

因为我们可以记录轮廓线因为右插头只有一种!

本质上我们记录的是n+1条线上有没有插头,而不是格子的信息!

那么也就是只需要合并上下状态相同的状态,因为我们只有下插头凸出来

所以能够合并信息QAQ

P5056 【模板】插头dp

括号表示法

记录线上的插头信息

左右括号相遇都可以消

消的时候有的要切换左右括号有的不用切换

然后这样枚举一下9种情况分类讨论即可

P3886 [JLOI2009]神秘的生物

最小表示法

考虑用一个8进制数记录连通块信息

这个是记录格子上的连通性,所以不毒瘤许多

每次考虑要不要合并两类信息

每次注意要新开的时候重赋编号

然后要写一个东西存状态

转移分类讨论,考虑所有的4种情况

其中上面有左边没有,这个格子不选的话一定要考虑其他线上有没有这个颜色的格子

李队推荐了一个很好写的做法

就是合并两个编号的时候,让 $min(a,b)=max(a,b)$

好题啊

$f_{i,j,S,a,b,c}$ 表示 $(i,j)$ 轮廓线轮廓为S,然后三个 $S,E,X$ 所在连通块标号为 $a,b,c$

然后转移的时候考虑合并a,b,c三个点所在连通块的标号就好了

时间复杂度 $O(n^5*8^n)$ ,n<=7可过

?题啊

黑白连通块要求不能有2*2的四连通

然后你可以染色,问方案数

记录轮廓线颜色和最小表示法

然后一个格子左上角的那个格子的信息也记录上去

初赛题

$dp_i$ 表示前i个数最大的子序列价值是什么

$f[S]$ 表示上一个选的数是S的最大价值

不优化dp数组转移,这个复杂度是 $O(值域*n)$

要么会在修改的时候TLE要么会在查询的时候TLE

考虑分块加速,前八位和后八位分块

你会发现只需要记录 $f_{S,T}$ 表示前八位为S位,然后最后上八位为T位的信息是什么,然后最大的价值是什么

那你会发现我们更新的时候花费 $O(T)$ 的复杂度来更新

然后查询的时候花费前八位 $O(S)$ 复杂度来更新即可

相当于均摊了查询和修改的复杂度

UNR#4序列妙妙值

$dp_{i,j}$ 表示前i个数划分成j段的最小代价

然后转移如果和值域联系起来的话可以用上述方法

$f_{k,S,T}$ 表示分了k段,然后前八位为S,后八位为T的最小代价

就和上个题一样了

An,m问 $\lfloor\frac{10^n}{m}\rfloor\%m$

有结论:

$\lfloor\frac{\lfloor \frac{x}{a} \rfloor}{b}\rfloor=\lfloor\frac{x}{ab}\rfloor$

证明:假设 $x\%ab =rem$

然后 $rem/a$ 不可能等于 $b$

然后我们展开变成这个式子 $\frac{10^n\%(m^2)-10\%(m)}{m}$

这个有循环节 $O(m^2)$ 即可

有解当且仅当 $a_i<=b_i$

•N个卡片，每个卡片正反面各有一个数字。

•你可以选正面或者反面的一个数字，问你最多能出现多少个不同的数字。

考虑每个卡片组成一个点,然后两两连接组成一个连通块

答案加上一个连通块中min(点数,边数)即可

ARC111B

找出一个置换环,即i想要 $p_i$ 的,然后 $p_i$ 想要 $p_{p_i}$

然后我们考虑让最大的那个匀给合法的下一个位置

然后我们减少了这个置换环的长度

然后不断的继续这个过程,直到置换环变为0

如果不能进行,就break

ARC111D

无向图,我们要给每条边定向,然后要保证每个点度数是 $C_i$

边 $(i,j)$ 如果 $c_i!=c_j$ 小的向大的连

否则是一个环

ARC111E

我抄题解可开心了

$i<=\lfloor\frac{D-2}{C-B}\rfloor$

然后你会发现,这个 $A+C*i,A+B*i$ 相当于两条直线

而且我们有合法的时候 $A+C*i-1/D-A+B*i/D=0$

因为此时两端线段长度差至多 $D-1$ 啊

于是我们就可以发现,不合法的时候就是其中有一个整点,而且至多一个整点

使用类欧,有:

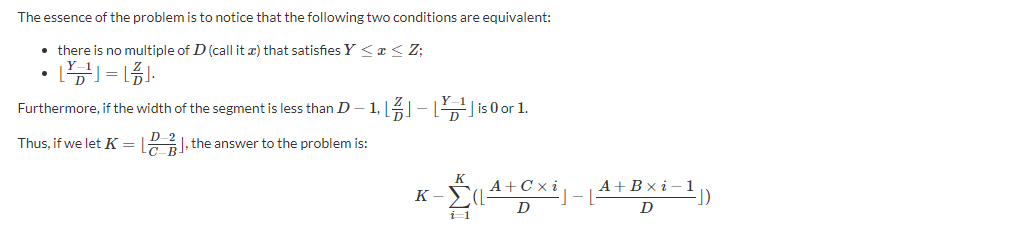
计算这个式子即可

AGC051A

考虑六边形一定是内部,方案数为1

然后每一层可以让偶数的边长+1或者奇数的边长+1

(1,d)走到(n,n)方案数

枚举即可

zhqwq负责内容:

SAM

学到许多:

NOI2017你的名字

注意本题中我们建出SAM后每个点随便用一个endpos去代表我这个节点的限制即可QAQ

弦论

每个点记录的是endpos等价类的大小,不是子树中本质不同的子串个数!

因为我们只看某个点代表的一个串,而不是这个点代表的所有串

而且我们走ch数组是在后面加入字符而不是跳!

跑匹配的时候,向fa跳要先减少已经匹配的长度!

因为这里是要看endpos是不是在某个地方,所以不要直接跳fail树啊,说不定就有了

直到这个点代表的串全跳完了才能fail

P4094 [HEOI2016/TJOI2016]字符串

定位出两个串,然后查询endpos是不是在这里面即可

重复旋律7

考虑有多少串指向了它

456有串5,45指向了它

其实就是ch数组连向他的那些,直接在dagdp即可

SAM

直接做是二分加倍增定位线段树合并会TLE

然后我们可发现其中二分可以省略掉变成直接双指针,以及倍增变成在sam上跳go和fa数组

线段树合并可以变成处理最靠前的出现endpos qaq

课后整理

最小循环节是 $lth=N-border[N]$

这不一定意味着原串是循环串,整除循环节就是

2375 [NOI2014] 动物园

首先记录上一次跳到的位置,沿用上一次的答案

然后新加入字符,考虑这个字符能不能延伸,如果能够延伸,而且小于一半就直接跳即可!

HDU-3746

找出最小循环节,然后补齐到最小循环节循环的最大程度即可

HUST-1010

最小循环节

CF825F String Compression

给定一个串s，其中重复出现的子串可以压缩成 “数字+重复的子串” 的形式，数字算长度。

只重复一次的串也要压。

求压缩后的最小长度。

$f_i=f_j+cst(i,j)$

$cst(i,j)$ 是区间循环串长,直接 $n^2$ 求border即可

1457 : 后缀自动机四·重复旋律7

这个就是上述我要用go数组完成的DAGdp啊...

所以还是直接统计答案即可!qwq

时间复杂度就是O(n)的

结构体里赋初值会CE(c++98)

4770 [NOI2018]你的名字

首先变成一个减

相当于我们要匹配一下T中多少串和 $[l,r]$ 代表的串匹配

就能知道每个前缀能选取的最长长度(限制)

试探的方法,每次要变成一个串在上面跑匹配,然后成功就长度加一,走ch,否则减少长度,长度跳光了才跳fail

CF1286E Fedya the Potter Strikes Back

建立fail树,相当于要维护所有还活着的 $border$ 信息

这个直接线段树支持区间取min,然后直接删掉一些下一个字符不是 $s_i$ 的,可以在后缀树上动态维护!

3975 [TJOI2015]弦论

siz和有两种方式,一个是所有不同endpos集合数

一个是所有不同的endpos集合中endpos元素个数

1449 : 后缀自动机三·重复旋律6

sam在长度线段树上区间加有个基本性质,长度串的答案比短的串答案小

所以差分的时候从后向前扫取max即可

4218 [CTSC2010]珠宝商

点分治,建立SAM可以做到 $O(m)$ 询问跨过一个分治重心的答案!

然后我们就可以用大的子树(大于根号n)建SAM做,

小于根号n的暴力 $n^2$ 枚举所有路径做即可

SAM做法就是我们先dfs将所有这个点走到的sam上的节点num++

也就是统计出[rt->u]形成的字符串加入字符rt后的位置

然后再统计[v->rt]形成的字符串,这个也是直接加入字符,但是是向前加入

所以此时是在SAM上trie树上的儿子

所以总复杂就是就是 $O(n+m)$

5341 [TJOI2019]甲苯先生和大中锋的字符串

给定S，问出现K次的子串中出现次数的最多的长度。

直接区间加几颗,不需要我们用什么性质

CF1063F String Journey

先设计一个dp,会发现反过来的话第i个串长度就是i

一定存在最优方案第i个串长为i

注意到双指针的性质

我们每次最多向后跳一步,但是可能向前跳很多步

定位节点还需要倍增!

然鹅注意你这个j的范围是 $<=i-lth$ 会发现我们可以双指针,也就是说我们虽然是单点修改这个区间最大值,但是我们并不需要删除

夏晓光(loveJY)的博客

ytez省队集训讲课第三轮